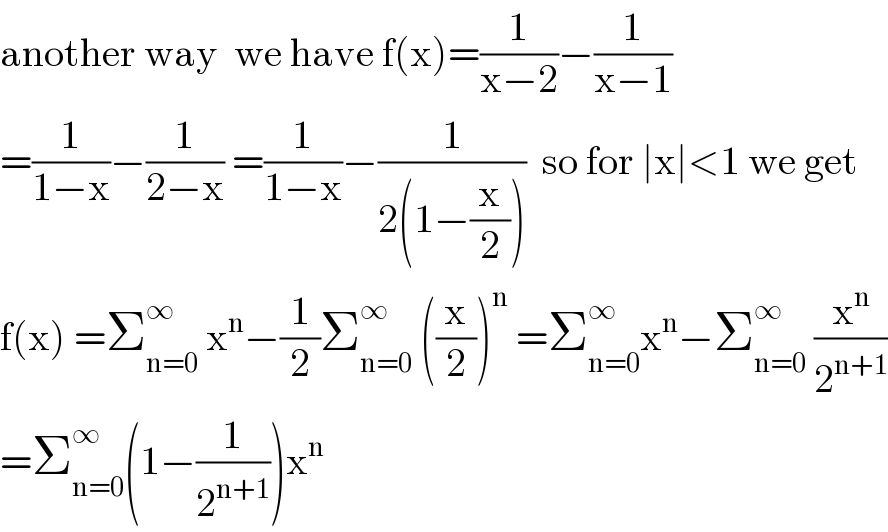Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 94337 by mathmax by abdo last updated on 18/May/20
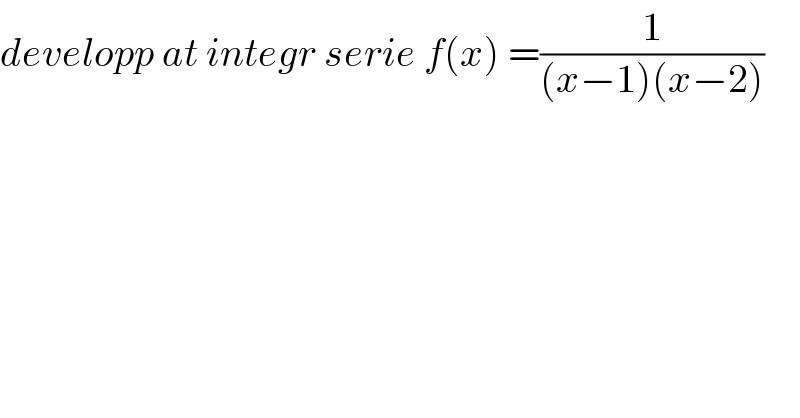
Answered by Rio Michael last updated on 18/May/20
![if you mean develope a series then: f(x) = (1/((x−1)(x−2))) ≡ (1/(x−2)) −(1/(x−1)) ⇒f(x) = (x−2)^(−1) −(x−1)^(−1) = x^(−1) (1−(2/x))^(−1) −x^(−1) (1−(1/x))^(−1) = x^(−1) [1 + (2/x) + (4/x^2 )+...]−x^(−1) [1 + (1/x) + (1/x^2 ) + ...] = (1/x) + (2/x^2 ) + ... −(1/x)−(1/x^2 ) −... = (1/x^2 ) +... ∣(2/x)∣ < 1](Q94349.png)
Commented by mathmax by abdo last updated on 18/May/20

Answered by mathmax by abdo last updated on 18/May/20
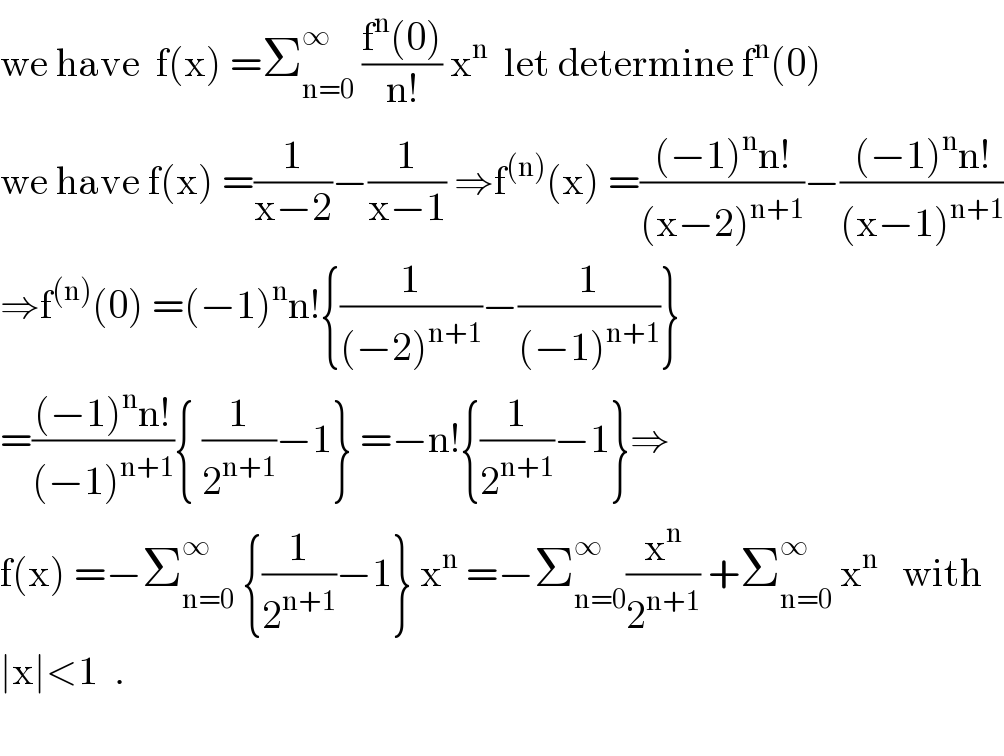
Answered by mathmax by abdo last updated on 18/May/20