Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 94573 by Ar Brandon last updated on 19/May/20

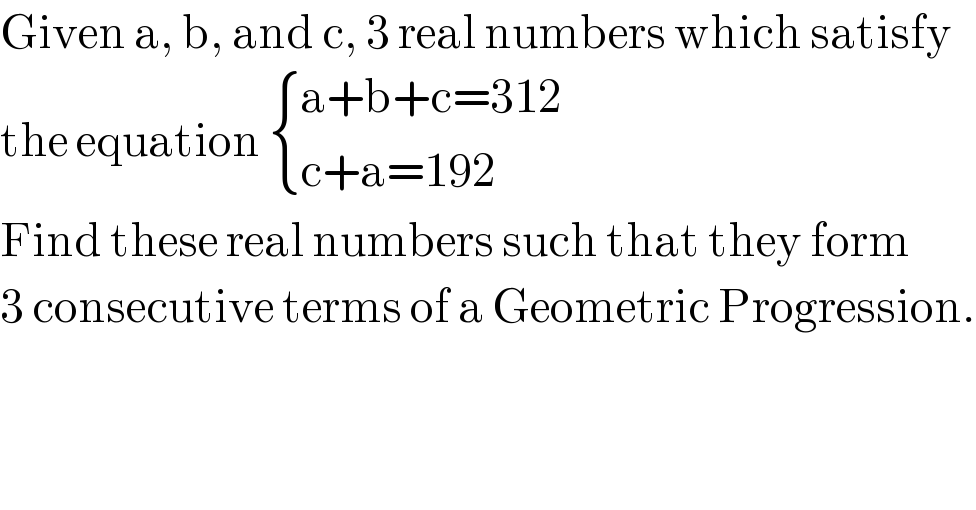
Given a, b, and c, 3 real numbers which satisfy the equation { ((a+b+c=312)),((c+a=192)) :} Find these real numbers such that they form 3 consecutive terms of a Geometric Progression.

$$\mathrm{Given}\:\mathrm{a},\:\mathrm{b},\:\mathrm{and}\:\mathrm{c},\:\mathrm{3}\:\mathrm{real}\:\mathrm{numbers}\:\mathrm{which}\:\mathrm{satisfy} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\begin{cases}{\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{312}}\\{\mathrm{c}+\mathrm{a}=\mathrm{192}}\end{cases} \\ $$$$\mathrm{Find}\:\mathrm{these}\:\mathrm{real}\:\mathrm{numbers}\:\mathrm{such}\:\mathrm{that}\:\mathrm{they}\:\mathrm{form} \\ $$$$\mathrm{3}\:\mathrm{consecutive}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{a}\:\mathrm{Geometric}\:\mathrm{Progression}. \\ $$

Commented by mr W last updated on 19/May/20

a=(b/r) c=br ac=b^2 =192 ⇒b=±8(√3) (b/r)+b+br=312 (1/r)+r+1=((312)/b) r^2 −(1−((312)/b))r+1=0 r=(1/2)[1−((312)/b)±(√((1−((312)/b))^2 −4))] r=(1/2)[1±13(√3)±(√((1±13(√3))^2 −4))]

$${a}=\frac{{b}}{{r}} \\ $$$${c}={br} \\ $$$${ac}={b}^{\mathrm{2}} =\mathrm{192} \\ $$$$\Rightarrow{b}=\pm\mathrm{8}\sqrt{\mathrm{3}} \\ $$$$\frac{{b}}{{r}}+{b}+{br}=\mathrm{312} \\ $$$$\frac{\mathrm{1}}{{r}}+{r}+\mathrm{1}=\frac{\mathrm{312}}{{b}} \\ $$$${r}^{\mathrm{2}} −\left(\mathrm{1}−\frac{\mathrm{312}}{{b}}\right){r}+\mathrm{1}=\mathrm{0} \\ $$$${r}=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{1}−\frac{\mathrm{312}}{{b}}\pm\sqrt{\left(\mathrm{1}−\frac{\mathrm{312}}{{b}}\right)^{\mathrm{2}} −\mathrm{4}}\right] \\ $$$${r}=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{1}\pm\mathrm{13}\sqrt{\mathrm{3}}\pm\sqrt{\left(\mathrm{1}\pm\mathrm{13}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{4}}\right] \\ $$

Commented by Ar Brandon last updated on 19/May/20

Thanks Mr W

Answered by Rasheed.Sindhi last updated on 19/May/20

Given a, b, and c, 3 real numbers which satisfy the equation { ((a+b+c=312)),((c+a=192)) :} Find these real numbers such that they form 3 consecutive terms of a Geometric Progression. a+b+c=312 ∧ c+a=192 b=312−192=120 ((120)/r) ,120 ,120r are in GP ((120)/r) +120 +120r=312 (1/r) +1+r=((312)/(120))=((13)/5) 5+5r+5r^2 =13r 5r^2 −8r+5=0 r=((8±(√(64−100)))/(10)) r is complex ∴a,c are not real.

$$\mathrm{Given}\:\mathrm{a},\:\mathrm{b},\:\mathrm{and}\:\mathrm{c},\:\mathrm{3}\:\mathrm{real}\:\mathrm{numbers}\:\mathrm{which}\:\mathrm{satisfy} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\begin{cases}{\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{312}}\\{\mathrm{c}+\mathrm{a}=\mathrm{192}}\end{cases} \\ $$$$\mathrm{Find}\:\mathrm{these}\:\mathrm{real}\:\mathrm{numbers}\:\mathrm{such}\:\mathrm{that}\:\mathrm{they}\:\mathrm{form} \\ $$$$\mathrm{3}\:\mathrm{consecutive}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{a}\:\mathrm{Geometric}\:\mathrm{Progression}. \\ $$$$\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{312}\:\:\wedge\:\mathrm{c}+\mathrm{a}=\mathrm{192} \\ $$$$\mathrm{b}=\mathrm{312}−\mathrm{192}=\mathrm{120} \\ $$$$\frac{\mathrm{120}}{\mathrm{r}}\:,\mathrm{120}\:,\mathrm{120r}\:{are}\:{in}\:{GP} \\ $$$$\frac{\mathrm{120}}{\mathrm{r}}\:+\mathrm{120}\:+\mathrm{120r}=\mathrm{312} \\ $$$$\frac{\mathrm{1}}{\mathrm{r}}\:+\mathrm{1}+\mathrm{r}=\frac{\mathrm{312}}{\mathrm{120}}=\frac{\mathrm{13}}{\mathrm{5}} \\ $$$$\:\:\mathrm{5}+\mathrm{5r}+\mathrm{5r}^{\mathrm{2}} =\mathrm{13r} \\ $$$$\:\:\mathrm{5r}^{\mathrm{2}} −\mathrm{8r}+\mathrm{5}=\mathrm{0} \\ $$$$\:\:\:{r}=\frac{\mathrm{8}\pm\sqrt{\mathrm{64}−\mathrm{100}}}{\mathrm{10}} \\ $$$${r}\:{is}\:{complex} \\ $$$$\:\therefore{a},{c}\:{are}\:{not}\:{real}. \\ $$$$ \\ $$

Commented by mr W last updated on 19/May/20

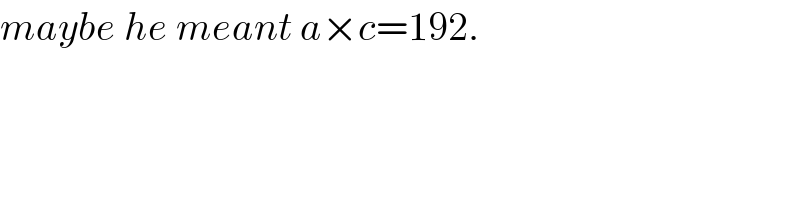
maybe he meant a×c=192.

$${maybe}\:{he}\:{meant}\:{a}×{c}=\mathrm{192}. \\ $$

Commented by Ar Brandon last updated on 19/May/20

Thank you I arrived at the same situation.

Commented by Ar Brandon last updated on 19/May/20

Oh no, it's a+b. I guess there was a problem with the question.

Terms of Service

Privacy Policy

Contact: info@tinkutara.com