
Question Number 85813 by jagoll last updated on 25/Mar/20
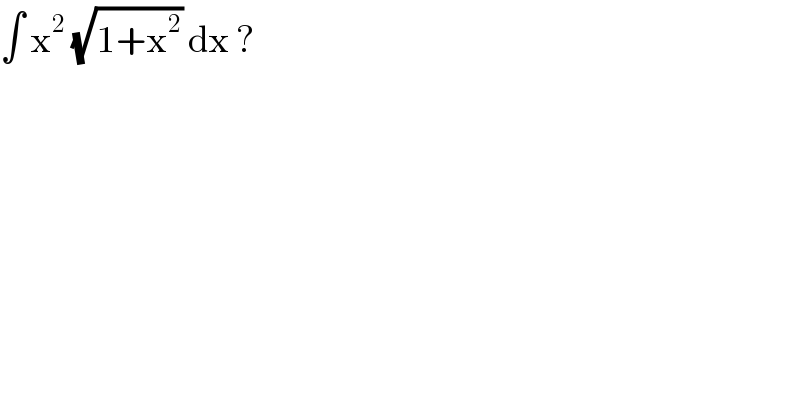
$$\int\:\mathrm{x}^{\mathrm{2}} \:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\:? \\ $$
Commented by jagoll last updated on 25/Mar/20
![∫ (1/2)x (2x(√(1+x^2 )) ) dx = ∫ (1/2)x (√(1+x^2 )) d(1+x^2 ) = (1/3)x (1+x^2 )^(3/2) −(1/3)∫ (1+x^2 )^(3/2) dx let J = ∫ (1+x^2 )^(3/2) dx [ x = tan t ] J = ∫ sec^5 t dt = sec^3 t tan t − ∫ 3 sec^5 t dt + ∫ 3sec^3 t dt 4J = sec^3 t tan t + 3 ( (1/2)sec t tan t −(1/2)ln∣sec t+tan t ∣) J = (1/4) sec^3 t tan t + (3/8) sec t tan t − (3/8) ln ∣ sec t + tan t∣](Q85816.png)
$$\int\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\:\left(\mathrm{2x}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\right)\:\mathrm{dx}\:=\: \\ $$$$\int\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{d}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}\:\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\int\:\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} \:\mathrm{dx} \\ $$$$\mathrm{let}\:\mathrm{J}\:=\:\int\:\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} \:\mathrm{dx} \\ $$$$\left[\:\mathrm{x}\:=\:\mathrm{tan}\:\mathrm{t}\:\right]\: \\ $$$$\mathrm{J}\:=\:\int\:\mathrm{sec}\:^{\mathrm{5}} \:\mathrm{t}\:\mathrm{dt}\: \\ $$$$=\:\mathrm{sec}\:^{\mathrm{3}} \mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:−\:\int\:\mathrm{3}\:\mathrm{sec}\:^{\mathrm{5}} \mathrm{t}\:\mathrm{dt}\:+\:\int\:\mathrm{3sec}\:^{\mathrm{3}} \:\mathrm{t}\:\mathrm{dt} \\ $$$$\mathrm{4J}\:=\:\mathrm{sec}\:^{\mathrm{3}} \:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:+\:\mathrm{3}\:\left(\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{sec}\:\mathrm{t}+\mathrm{tan}\:\mathrm{t}\:\mid\right)\: \\ $$$$\mathrm{J}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{sec}\:^{\mathrm{3}} \:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:+\:\frac{\mathrm{3}}{\mathrm{8}}\:\mathrm{sec}\:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:−\: \\ $$$$\frac{\mathrm{3}}{\mathrm{8}}\:\mathrm{ln}\:\mid\:\mathrm{sec}\:\mathrm{t}\:+\:\mathrm{tan}\:\:\mathrm{t}\mid\: \\ $$
Answered by john santu last updated on 25/Mar/20
![let x = sinh t ⇒dx = cosh t dt I = ∫ sinh^2 t cosh t (cosh t dt) = ∫ sinh^2 t cosh^2 t dt = (1/4)∫ sinh^2 2t dt = (1/8) ∫ (cosh 4t−1) dt = (1/8) (((sinh 4t)/4) − t ) + c = (1/8) [( sinh t cosh t)(1+2sinh^2 t)−t ] +c = (1/8) [ (x(√(1+x^2 )) )(1+2x^2 )−sinh^(−1) x] + c](Q85814.png)
$${let}\:{x}\:=\:\mathrm{sinh}\:{t}\:\Rightarrow{dx}\:=\:\mathrm{cosh}\:{t}\:{dt} \\ $$$${I}\:=\:\int\:\mathrm{sinh}\:^{\mathrm{2}} {t}\:\mathrm{cosh}\:{t}\:\left(\mathrm{cosh}\:{t}\:{dt}\right) \\ $$$$=\:\int\:\mathrm{sinh}\:^{\mathrm{2}} {t}\:\mathrm{cosh}\:^{\mathrm{2}} {t}\:{dt}\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\int\:\mathrm{sinh}\:^{\mathrm{2}} \:\mathrm{2}{t}\:{dt}\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{8}}\:\int\:\left(\mathrm{cosh}\:\mathrm{4}{t}−\mathrm{1}\right)\:{dt} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{8}}\:\left(\frac{\mathrm{sinh}\:\mathrm{4}{t}}{\mathrm{4}}\:−\:{t}\:\right)\:+\:{c} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{8}}\:\left[\left(\:\mathrm{sinh}\:{t}\:\mathrm{cosh}\:{t}\right)\left(\mathrm{1}+\mathrm{2sinh}\:^{\mathrm{2}} {t}\right)−{t}\:\right]\:+{c} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{8}}\:\left[\:\left({x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right)\left(\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} \right)−\mathrm{sinh}\:^{−\mathrm{1}} \:{x}\right]\:+\:{c} \\ $$
Commented by jagoll last updated on 25/Mar/20

$$\mathrm{waw}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{try}\:\mathrm{via}\:\mathrm{integration} \\ $$$$\mathrm{by}\:\mathrm{parts} \\ $$
Answered by MJS last updated on 25/Mar/20
![∫x^2 (√(1+x^2 ))dx= [x=sinh ln t =((t^2 −1)/(2t)) ⇔ t=x+(√(x^2 +1)) → dx=((t^2 +1)/(2t^2 ))] =(1/(16))∫t^3 dt−(1/8)∫(dt/t)+(1/(16))∫(dt/t^5 )= =(1/(64))t^4 −(1/8)ln t −(1/(64t^4 ))=((t^8 −1)/(64t^4 ))−(1/8)ln t = =(1/8)(x(2x^2 +1)(√(x^2 +1))−ln (x+(√(x^2 +1)))) +C](Q85847.png)
$$\int{x}^{\mathrm{2}} \sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{x}=\mathrm{sinh}\:\mathrm{ln}\:{t}\:=\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{t}}\:\Leftrightarrow\:{t}={x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dx}=\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\int{t}^{\mathrm{3}} {dt}−\frac{\mathrm{1}}{\mathrm{8}}\int\frac{{dt}}{{t}}+\frac{\mathrm{1}}{\mathrm{16}}\int\frac{{dt}}{{t}^{\mathrm{5}} }= \\ $$$$=\frac{\mathrm{1}}{\mathrm{64}}{t}^{\mathrm{4}} −\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:{t}\:−\frac{\mathrm{1}}{\mathrm{64}{t}^{\mathrm{4}} }=\frac{{t}^{\mathrm{8}} −\mathrm{1}}{\mathrm{64}{t}^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:{t}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left({x}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)\right)\:+{C} \\ $$
Commented by jagoll last updated on 25/Mar/20
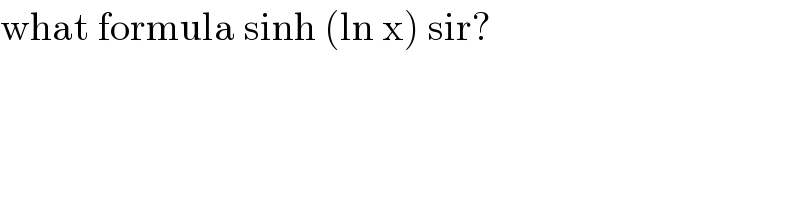
$$\mathrm{what}\:\mathrm{formula}\:\mathrm{sinh}\:\left(\mathrm{ln}\:\mathrm{x}\right)\:\mathrm{sir}? \\ $$
Commented by MJS last updated on 25/Mar/20

$$\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{as}\:\mathrm{it}\:\mathrm{is} \\ $$$$\mathrm{I}\:\mathrm{had}\:\mathrm{the}\:\mathrm{idea}\:\mathrm{to}\:\mathrm{use}\:\mathrm{this}\:\mathrm{when}\:\mathrm{I}\:\mathrm{had}\:\mathrm{to} \\ $$$$\mathrm{solve}\:\mathrm{integrals}\:\mathrm{in}\:\mathrm{2}\:\mathrm{steps},\:\mathrm{1}^{\mathrm{st}} \:\mathrm{a}\:\mathrm{hyperbolic} \\ $$$$\mathrm{substitution},\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{get}\:\mathrm{rid}\:\mathrm{of}\:\mathrm{e}^{{t}} .\:\mathrm{you}\:\mathrm{can}\:\mathrm{do} \\ $$$$\mathrm{it}\:\mathrm{in}\:\mathrm{one}\:\mathrm{step} \\ $$
