
Question Number 9470 by tawakalitu last updated on 09/Dec/16
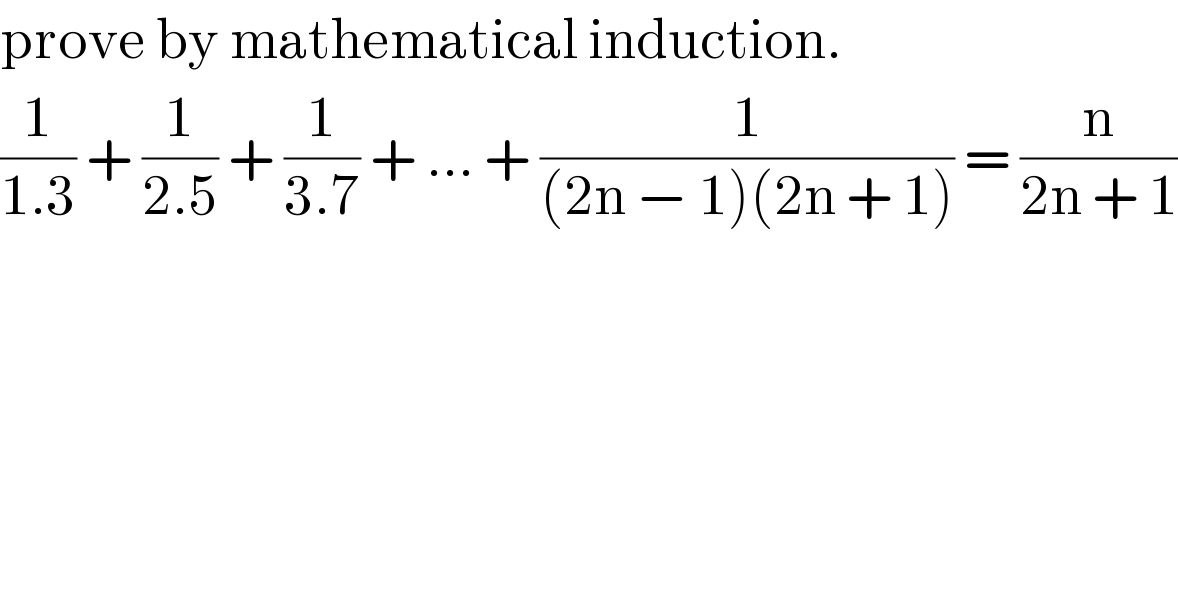
$$\mathrm{prove}\:\mathrm{by}\:\mathrm{mathematical}\:\mathrm{induction}. \\ $$$$\frac{\mathrm{1}}{\mathrm{1}.\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{2}.\mathrm{5}}\:+\:\frac{\mathrm{1}}{\mathrm{3}.\mathrm{7}}\:+\:...\:+\:\frac{\mathrm{1}}{\left(\mathrm{2n}\:−\:\mathrm{1}\right)\left(\mathrm{2n}\:+\:\mathrm{1}\right)}\:=\:\frac{\mathrm{n}}{\mathrm{2n}\:+\:\mathrm{1}} \\ $$
Commented by mrW last updated on 10/Dec/16
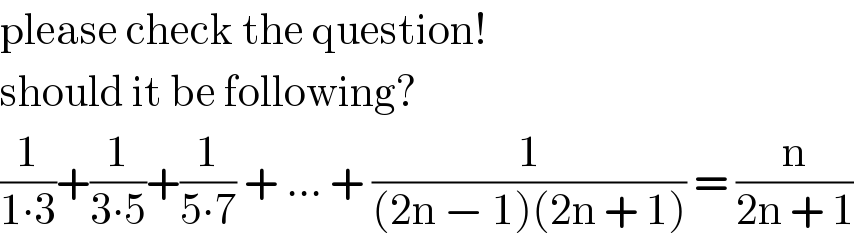
$$\mathrm{please}\:\mathrm{check}\:\mathrm{the}\:\mathrm{question}! \\ $$$$\mathrm{should}\:\mathrm{it}\:\mathrm{be}\:\mathrm{following}? \\ $$$$\frac{\mathrm{1}}{\mathrm{1}\centerdot\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}\centerdot\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}\centerdot\mathrm{7}}\:+\:...\:+\:\frac{\mathrm{1}}{\left(\mathrm{2n}\:−\:\mathrm{1}\right)\left(\mathrm{2n}\:+\:\mathrm{1}\right)}\:=\:\frac{\mathrm{n}}{\mathrm{2n}\:+\:\mathrm{1}} \\ $$
Commented by tawakalitu last updated on 10/Dec/16
$$\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{like}\:\mathrm{this} \\ $$
Answered by mrW last updated on 10/Dec/16
![it is to prove S(n)=Σ_(k=1) ^n (1/((2k−1)(2k+1)))=(n/(2n+1)) for n=1: S(1)=(1/(1×3))=(1/3)=^! (1/(2×1+1))=(1/3) ⇒it′s true suppose it′s true for n, we have for n+1 S(n+1)=S(n)+(1/([2(n+1)−1][2(n+1)+1])) =S(n)+(1/((2n+1)[2(n+1)+1])) =(n/(2n+1))+(1/((2n+1)[2(n+1)+1])) =((n[2(n+1)+1]+1)/((2n+1)[2(n+1)+1])) =((2n^2 +3n+1)/((2n+1)[2(n+1)+1])) =(((2n+1)(n+1))/((2n+1)[2(n+1)+1])) =(((n+1))/(2(n+1)+1)) that means it′s also true for n+1. ⇒it′s true for all n≥1.](Q9476.png)
$$\mathrm{it}\:\mathrm{is}\:\mathrm{to}\:\mathrm{prove} \\ $$$$\mathrm{S}\left(\mathrm{n}\right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\:\frac{\mathrm{1}}{\left(\mathrm{2k}−\mathrm{1}\right)\left(\mathrm{2k}+\mathrm{1}\right)}=\frac{\mathrm{n}}{\mathrm{2n}+\mathrm{1}} \\ $$$$ \\ $$$$\mathrm{for}\:\mathrm{n}=\mathrm{1}: \\ $$$$\mathrm{S}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{1}×\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}}\overset{!} {=}\frac{\mathrm{1}}{\mathrm{2}×\mathrm{1}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{it}'\mathrm{s}\:\mathrm{true} \\ $$$$ \\ $$$$\mathrm{suppose}\:\mathrm{it}'\mathrm{s}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n},\:\mathrm{we}\:\mathrm{have}\:\mathrm{for}\:\mathrm{n}+\mathrm{1} \\ $$$$\mathrm{S}\left(\mathrm{n}+\mathrm{1}\right)=\mathrm{S}\left(\mathrm{n}\right)+\frac{\mathrm{1}}{\left[\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)−\mathrm{1}\right]\left[\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{1}\right]} \\ $$$$=\mathrm{S}\left(\mathrm{n}\right)+\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)\left[\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{1}\right]} \\ $$$$=\frac{\mathrm{n}}{\mathrm{2n}+\mathrm{1}}+\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)\left[\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{1}\right]} \\ $$$$=\frac{\mathrm{n}\left[\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{1}\right]+\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)\left[\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{1}\right]} \\ $$$$=\frac{\mathrm{2n}^{\mathrm{2}} +\mathrm{3n}+\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)\left[\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{1}\right]} \\ $$$$=\frac{\left(\mathrm{2n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{1}\right)}{\left(\mathrm{2n}+\mathrm{1}\right)\left[\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{1}\right]} \\ $$$$=\frac{\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{1}} \\ $$$$\mathrm{that}\:\mathrm{means}\:\mathrm{it}'\mathrm{s}\:\mathrm{also}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n}+\mathrm{1}. \\ $$$$\Rightarrow\mathrm{it}'\mathrm{s}\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:\mathrm{n}\geqslant\mathrm{1}. \\ $$
Commented by tawakalitu last updated on 10/Dec/16
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\: \\ $$$$\mathrm{effort}. \\ $$
