∫(dx/(x+(√x))) (2,3)=?


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 94811 by Abdulrahman last updated on 21/May/20

$\int \frac{dx}{x + \sqrt{x}} (2, 3) = ?$
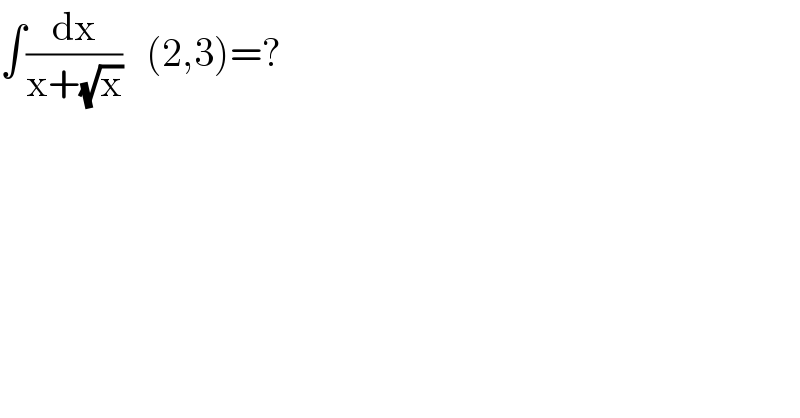
	Answered by ElOuafi last updated on 21/May/20

	$\int \frac{d x}{x + \sqrt{x}} = \int \frac{d x}{\sqrt{x} (\sqrt{x} + 1)} = \int \frac{\frac{2}{2 \sqrt{x}}}{\sqrt{x} + 1} d x = 2 \int \frac{d (\sqrt{x} + 1)}{\sqrt{x} + 1}$ $p u t u = \sqrt{x} + 1 \Rightarrow= 2 \int \frac{d u}{u}$ $= 2 l n (\sqrt{x} + 1) + c$ $s o \int_{2}^{3} \frac{d x}{x + \sqrt{x}} = 2 l n (\frac{\sqrt{3} + 1}{\sqrt{2} + 1})$
	Commented by Abdulrahman last updated on 21/May/20

	$thanks alot$
	Answered by i jagooll last updated on 21/May/20
	$let (√(x ))=t ⇒x=t^2 ; dx = 2t dt ∫ ((2t dt)/(t^2 +t)) = ∫ ((2 dt)/(t+1)) = 2 ln ∣t+1∣ = 2[ ln ∣1+(√x) ∣ ]_2 ^3 = 2 {ln (1+(√3))−ln(1+(√2)) } = 2 ln (((1+(√3))/(1+(√2))))$
	$let \sqrt{x} = t \Rightarrow x = t^{2}; dx = 2 t dt$ $\int \frac{2 t dt}{t^{2} + t} = \int \frac{2 dt}{t + 1} = 2 \ln ∣ t + 1 ∣$ $= 2 {[\ln ∣ 1 + \sqrt{x} ∣]}_{2}^{3}$ $= 2 {\ln (1 + \sqrt{3}) - \ln (1 + \sqrt{2})}$ $= 2 \ln (\frac{1 + \sqrt{3}}{1 + \sqrt{2}})$
	Commented by Abdulrahman last updated on 21/May/20

	$thanks alot$
	Answered by mathmax by abdo last updated on 21/May/20

	$I = \int_{2}^{3} \frac{dx}{x + \sqrt{x}} we do the changement \sqrt{x} = t \Rightarrow$ $I = \int_{\sqrt{2}}^{\sqrt{3}} \frac{2 tdt}{t^{2} + t} = 2 \int_{\sqrt{2}}^{\sqrt{3}} \frac{dt}{t + 1} = 2 {[\ln (t + 1)]}_{\sqrt{2}}^{\sqrt{3}} = 2 (\ln (1 + \sqrt{3}) - \ln (1 + \sqrt{2}))$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum