
Question Number 94907 by mathmax by abdo last updated on 21/May/20
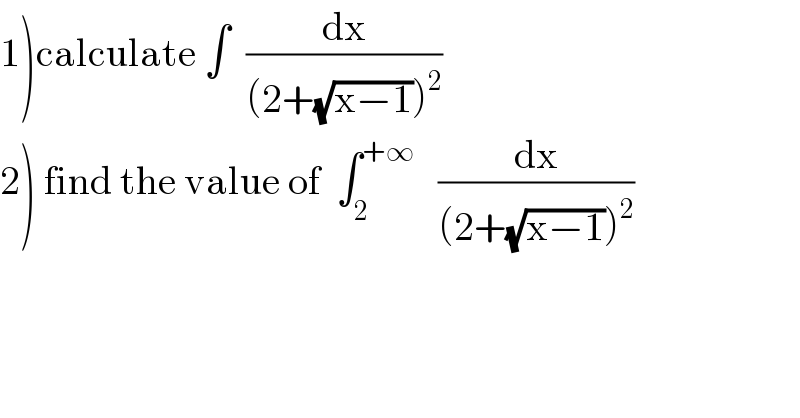
$$\left.\mathrm{1}\right)\mathrm{calculate}\:\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{2}+\sqrt{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{2}\right)\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\:\int_{\mathrm{2}} ^{+\infty} \:\:\:\frac{\mathrm{dx}}{\left(\mathrm{2}+\sqrt{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{2}} } \\ $$
Answered by MJS last updated on 22/May/20
![∫(dx/((2+(√(x−1)))^2 ))= [t=2+(√(x−1)) → dx=2(√(x−1))dt] =2∫((t−2)/t^2 )dt=(4/t)+2ln t = =(4/(2+(√(x−1))))+2ln (2+(√(x−1))) +C ∫_2 ^∞ (dx/((2+(√(x−1)))^2 )) diverges](Q94988.png)
$$\int\frac{{dx}}{\left(\mathrm{2}+\sqrt{{x}−\mathrm{1}}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{2}+\sqrt{{x}−\mathrm{1}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}−\mathrm{1}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{t}−\mathrm{2}}{{t}^{\mathrm{2}} }{dt}=\frac{\mathrm{4}}{{t}}+\mathrm{2ln}\:{t}\:= \\ $$$$=\frac{\mathrm{4}}{\mathrm{2}+\sqrt{{x}−\mathrm{1}}}+\mathrm{2ln}\:\left(\mathrm{2}+\sqrt{{x}−\mathrm{1}}\right)\:+{C} \\ $$$$\underset{\mathrm{2}} {\overset{\infty} {\int}}\frac{{dx}}{\left(\mathrm{2}+\sqrt{{x}−\mathrm{1}}\right)^{\mathrm{2}} }\:\mathrm{diverges} \\ $$
Commented by mathmax by abdo last updated on 22/May/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{mjs} \\ $$
Answered by mathmax by abdo last updated on 22/May/20
![1) I =∫ (dx/((2+(√(x−1)))^2 )) changement (√(x−1))=t give x−1=t^2 ⇒ I =∫ ((2tdt)/((2+t)^2 )) = ∫ ((2tdt)/(t^2 +4t +4)) =∫ ((2t+4−4)/(t^2 +4t +4))dt=∫((2t+4)/(t^2 +4t+4))dt −4∫ (dt/(t^2 +4t +4)) =ln(t^2 +4t+4)−4 ∫ (dt/((t+2)^2 )) =2ln∣t+2∣+(4/(t+2)) +C =2ln∣(√(x−1))+2∣+(4/((√(x−1))+2)) +C 2) ∫_2 ^(+∞) (dx/((2+(√(x−1)))^2 )) =[2ln∣(√(x−1))+2∣ +(4/((√(x−1))+2))]_2 ^(+∞) =+∞ so this integrale is divergente .!](Q95037.png)
$$\left.\mathrm{1}\right)\:\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{2}+\sqrt{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{2}} }\:\:\mathrm{changement}\:\sqrt{\mathrm{x}−\mathrm{1}}=\mathrm{t}\:\mathrm{give}\:\mathrm{x}−\mathrm{1}=\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\frac{\mathrm{2tdt}}{\left(\mathrm{2}+\mathrm{t}\right)^{\mathrm{2}} }\:=\:\int\:\:\frac{\mathrm{2tdt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{4t}\:+\mathrm{4}}\:=\int\:\:\frac{\mathrm{2t}+\mathrm{4}−\mathrm{4}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{4t}\:+\mathrm{4}}\mathrm{dt}=\int\frac{\mathrm{2t}+\mathrm{4}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{4t}+\mathrm{4}}\mathrm{dt} \\ $$$$−\mathrm{4}\int\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{4t}\:+\mathrm{4}}\:=\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{4t}+\mathrm{4}\right)−\mathrm{4}\:\int\:\frac{\mathrm{dt}}{\left(\mathrm{t}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{2ln}\mid\mathrm{t}+\mathrm{2}\mid+\frac{\mathrm{4}}{\mathrm{t}+\mathrm{2}}\:+\mathrm{C}\:\:=\mathrm{2ln}\mid\sqrt{\mathrm{x}−\mathrm{1}}+\mathrm{2}\mid+\frac{\mathrm{4}}{\sqrt{\mathrm{x}−\mathrm{1}}+\mathrm{2}}\:+\mathrm{C} \\ $$$$\left.\mathrm{2}\right)\:\int_{\mathrm{2}} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{2}+\sqrt{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{2}} }\:=\left[\mathrm{2ln}\mid\sqrt{\mathrm{x}−\mathrm{1}}+\mathrm{2}\mid\:+\frac{\mathrm{4}}{\sqrt{\mathrm{x}−\mathrm{1}}+\mathrm{2}}\right]_{\mathrm{2}} ^{+\infty} \:=+\infty \\ $$$$\mathrm{so}\:\mathrm{this}\:\mathrm{integrale}\:\mathrm{is}\:\mathrm{divergente}\:.! \\ $$
