Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 95060 by EmericGent last updated on 22/May/20

$$Evaluate$$$${\int }_0^{\mathrm{\infty }}arcsin\left(e^{-x}\right)dx$$$${\int }_0^{\mathrm{\infty }}arccos(1-2e^{-x})dx$$$$andStepUp$$$$Evaluate$$$${\int }_0^{\mathrm{\infty }}arccos(1-e^{-x})dx$$$${\int }_{-t}^{t}arctan\left(e^{-x}\right)dx$$

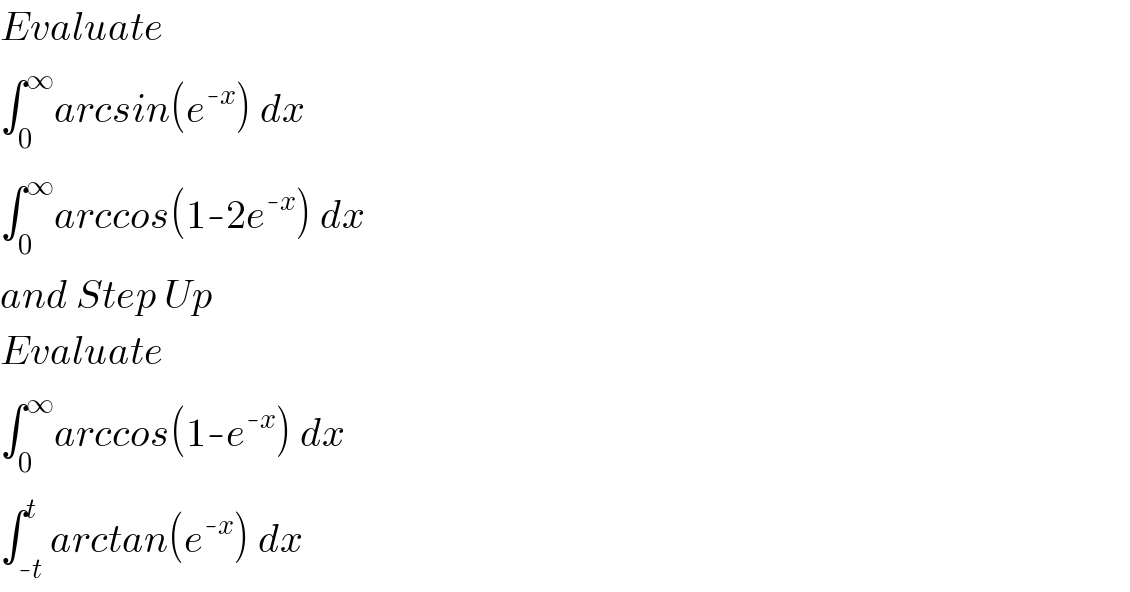
Answered by mathmax by abdo last updated on 23/May/20

$$\mathrm{let}\mathrm{take}\mathrm{a}\mathrm{try}\mathrm{I}={\int }_0^{\mathrm{\infty }}\arcsin \left({\mathrm{e}}^{-\mathrm{x}}\right)\mathrm{dx}\mathrm{changement}{\mathrm{e}}^{-\mathrm{x}}=\mathrm{t}\mathrm{give}\mathrm{x}=-\mathrm{lnt}\Rightarrow$$$$\mathrm{I}={\int }_0^1\arcsin \left(\mathrm{t}\right)\frac{\mathrm{dt}}{\mathrm{t}}={\int }_0^1\frac{\arcsin \left(\mathrm{t}\right)}{\mathrm{t}}\mathrm{dt}\mathrm{let}\mathrm{f}\left(\mathrm{x}\right)={\int }_0^1\frac{\arcsin \left(\mathrm{xt}\right)}{\mathrm{t}}\mathrm{dt}(\mathrm{x}>0)$$$${\mathrm{f}}^{{}^{\prime }}\left(\mathrm{x}\right)={\int }_0^1\frac{\mathrm{t}}{\mathrm{t}\sqrt{1-{\mathrm{x}}^2{\mathrm{t}}^2}}\mathrm{dt}={\int }_0^1\frac{\mathrm{dt}}{\sqrt{1-{\left(\mathrm{xt}\right)}^2}}{=}_{\mathrm{xt}=\sin \alpha }{\int }_0^{\mathrm{arcsinx}}\frac{1}{\mathrm{x}\cos \alpha }\times \frac{1}{\mathrm{x}}\cos \alpha \mathrm{d}\alpha$$$$=\frac{\arcsin \left(\mathrm{x}\right)}{{\mathrm{x}}^2}\Rightarrow \mathrm{f}\left(\mathrm{x}\right)={\int }_1^{\mathrm{x}}\frac{\arcsin \left(\mathrm{u}\right)}{{\mathrm{u}}^2}\mathrm{du}+\mathrm{c}$$$$={[-\frac{1}{\mathrm{u}}\mathrm{arcsinu}]}_1^{\mathrm{x}}-{\int }_1^{\mathrm{x}}(-\frac{1}{\mathrm{u}})\times \frac{1}{\sqrt{1-{\mathrm{u}}^2}}\mathrm{du}+\mathrm{c}$$$$=\frac{\pi }{2}-\frac{\mathrm{arcsinx}}{\mathrm{x}}+{\int }_1^{\mathrm{x}}\frac{\mathrm{du}}{\mathrm{u}\sqrt{1-{\mathrm{u}}^2}}\mathrm{but}$$$${\int }_1^{\mathrm{x}}\frac{\mathrm{du}}{\mathrm{u}\sqrt{1-{\mathrm{u}}^2}}{=}_{\mathrm{u}=\mathrm{sinz}}{\int }_{\frac{\pi }{2}}^{\mathrm{arcsinx}}\frac{\mathrm{cosz}}{\mathrm{sinz}\mathrm{cosz}}\mathrm{dz}={\int }_{\frac{\pi }{2}}^{\mathrm{arcsinx}}\frac{\mathrm{dz}}{\mathrm{sinz}}$$$${=}_{\tan \left(\frac{\mathrm{z}}{2}\right)=\lambda }{\int }_{\mathrm{\infty }}^{\tan \left(\frac{\mathrm{arcsinx}}{2}\right)}\frac{2\mathrm{d}\lambda }{(1+{\lambda }^2)\times \frac{2\lambda }{1+{\lambda }^2}}=-{\int }_{\tan \left(\frac{\mathrm{arcsinx}}{2}\right)}\frac{\mathrm{d}\lambda }{\lambda }$$$$=-\ln \mid \tan \left(\frac{\mathrm{arcsinx}}{2}\right)\mid \Rightarrow$$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\pi }{2}-\frac{\mathrm{arcsinx}}{\mathrm{x}}-\ln \mid \tan \left(\frac{\mathrm{arcsinx}}{2}\right)\mid +\mathrm{c}$$$$\mathrm{f}\left(1\right)=\mathrm{c}={\int }_0^1\frac{\mathrm{arcsint}}{\mathrm{t}}\mathrm{dt}\Rightarrow$$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\pi }{2}-\frac{\mathrm{arcsinx}}{\mathrm{x}}-\ln \mid \tan \left(\frac{\mathrm{arcsinx}}{2}\right)\mid +{\int }_0^1\frac{\mathrm{arcsint}}{\mathrm{t}}\mathrm{dt}\mathrm{for}\mathrm{x}>0$$$$\mathrm{f}\left(\frac{1}{\mathrm{x}}\right)=\frac{\pi }{2}-\frac{\frac{\pi }{2}-\mathrm{arcosx}}{\mathrm{x}}-\ln \mid \tan \left(\frac{\frac{\pi }{2}-\mathrm{arcosx}}{2}\right)\mid +{\int }_0^1\frac{\mathrm{arcsint}}{\mathrm{t}}\mathrm{dt}$$$$=\frac{\pi }{2}-\frac{\pi }{2\mathrm{x}}+\frac{\mathrm{arcosx}}{\mathrm{x}}-\ln \mid \tan (\frac{\pi }{4}-\frac{\mathrm{arcosx}}{2})\mid +{\int }_0^1\frac{\mathrm{arcsint}}{\mathrm{t}}\mathrm{dt}$$$$...\mathrm{be}\mathrm{continued}...$$

Commented by mathmax by abdo last updated on 23/May/20

$$\mathrm{let}\mathrm{find}{\int }_0^1\frac{\mathrm{arcsint}}{\mathrm{t}}\mathrm{dt}\mathrm{at}\mathrm{form}\mathrm{of}\mathrm{serie}\mathrm{we}\mathrm{have}$$$$\mathrm{arcsint}=\sum _{\mathrm{n}=0}^{\mathrm{\infty }}\frac{\left(2\mathrm{n}\right)!}{(2\mathrm{n}+1)2^{2\mathrm{n}}{(\mathrm{n}!)}^2}{\mathrm{t}}^{2\mathrm{n}+1}$$$$=\mathrm{t}+\frac{2!}{3.4.}{\mathrm{t}}^3+\frac{4!}{5.16{(2!)}^2}+....\Rightarrow \frac{\mathrm{arcsint}}{\mathrm{t}}=\sum _{\mathrm{n}=0}^{\mathrm{\infty }}\frac{\left(2\mathrm{n}\right)!}{(2\mathrm{n}+1)2^{2\mathrm{n}}{(\mathrm{n}!)}^2}{\mathrm{t}}^{2\mathrm{n}}\Rightarrow$$$${\int }_0^1\frac{\mathrm{arcsint}}{\mathrm{t}}\mathrm{dt}=\sum _{\mathrm{n}=0}^{\mathrm{\infty }}\frac{\left(2\mathrm{n}\right)!}{{(2\mathrm{n}+1)}^2{2}^{2\mathrm{n}}{(\mathrm{n}!)}^2}$$$$=1+\frac{2!}{3^2.2^2{(1!)}^2}+\frac{4!}{5^2.2^4{(2!)}^2}+....$$

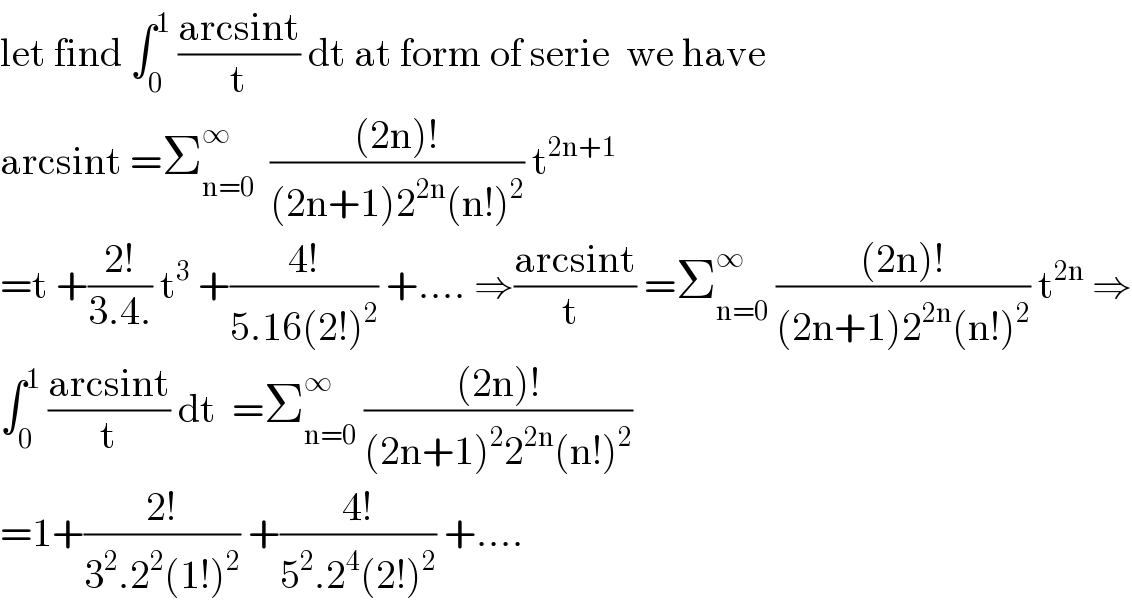
Commented by EmericGent last updated on 23/May/20

I used a much easier way (I show you my start)

Commented by EmericGent last updated on 23/May/20

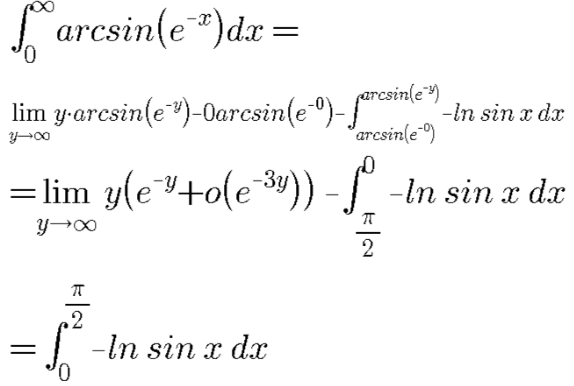
Commented by mathmax by abdo last updated on 23/May/20

$$\mathrm{A}\left(\mathrm{y}\right)={\int }_0^{\mathrm{y}}\arcsin \left({\mathrm{e}}^{-\mathrm{x}}\right)\mathrm{dx}\mathrm{by}\mathrm{parts}$$$$\mathrm{A}\left(\mathrm{y}\right)={\left[\mathrm{x}\arcsin \left({\mathrm{e}}^{-\mathrm{x}}\right)\right]}_0^{\mathrm{y}}-{\int }_0^{\mathrm{y}}\mathrm{x}\left(\frac{-{\mathrm{e}}^{-\mathrm{x}}}{\sqrt{1-{\mathrm{e}}^{-2\mathrm{x}}}}\right)\mathrm{dx}$$$$=\mathrm{y}\arcsin \left({\mathrm{e}}^{-\mathrm{y}}\right)+{\int }_0^{\mathrm{y}}\frac{{\mathrm{xe}}^{-\mathrm{x}}}{\sqrt{1-{\mathrm{e}}^{-2\mathrm{x}}}}\mathrm{dx}{\mathrm{e}}^{-\mathrm{x}}=\sin \alpha \Rightarrow -\mathrm{x}=\ln \left(\sin \alpha \right)\Rightarrow$$$${\int }_0^{\mathrm{y}}\frac{{\mathrm{xe}}^{-\mathrm{x}}}{\sqrt{1-{\mathrm{e}}^{-2\mathrm{x}}}}\mathrm{dx}={\int }_{\frac{\pi }{2}}^{\arcsin \left({\mathrm{e}}^{-\mathrm{y}}\right)}\frac{\left(\ln \left(\sin \alpha \right)\right)\sin \alpha }{\cos \alpha }\times \frac{\cos \alpha }{\sin \alpha }\mathrm{d}\alpha$$$$=-{\int }_{\arcsin \left({\mathrm{e}}^{-\mathrm{y}}\right)}^{\frac{\pi }{2}}\ln \left(\sin \alpha \right)\mathrm{d}\alpha \Rightarrow \mathrm{A}\left(\mathrm{y}\right)=\mathrm{y}\arcsin \left({\mathrm{e}}^{-\mathrm{y}}\right)-{\int }_{\arcsin \left({\mathrm{e}}^{-\mathrm{y}}\right)}^{\frac{\pi }{2}}\ln \left(\sin \alpha \right)\mathrm{d}\alpha$$$${\lim }_{\mathrm{y}\to +\mathrm{\infty }}\mathrm{A}\left(\mathrm{y}\right)=-{\int }_0^{\frac{\pi }{2}}\ln \left(\sin \alpha \right)\mathrm{d}\alpha =-(-\frac{\pi }{2}\ln \left(2\right))\Rightarrow$$$${\int }_0^{\mathrm{\infty }}\arcsin \left({\mathrm{e}}^{-\mathrm{x}}\right)\mathrm{dx}=\frac{\pi }{2}\ln \left(2\right)$$

Commented by mathmax by abdo last updated on 23/May/20

$$\mathrm{your}\mathrm{method}\mathrm{is}\mathrm{correct}\mathrm{sir}\mathrm{thanks}.$$

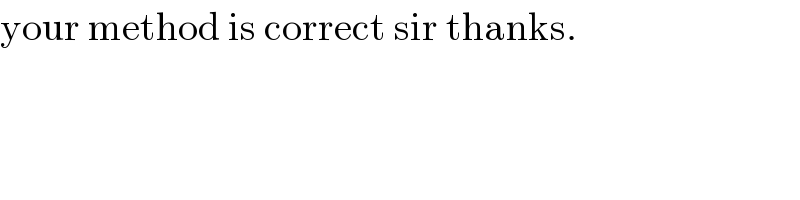
Commented by EmericGent last updated on 23/May/20

I did the second and the third by the same way (actually I'm a boy)

Answered by abdomathmax last updated on 23/May/20

$$\mathrm{A}\left(\mathrm{y}\right)={\int }_0^{\mathrm{y}}\mathrm{arcos}(1-{2\mathrm{e}}^{-\mathrm{x}})\mathrm{dx}\mathrm{by}\mathrm{parts}$$$$\mathrm{A}\left(\mathrm{y}\right)={\left[\mathrm{x}\mathrm{arcos}(1-{2\mathrm{e}}^{-\mathrm{x}})\right]}_0^{\mathrm{y}}+{\int }_0^{\mathrm{y}}\mathrm{x}\times \frac{{2\mathrm{e}}^{-\mathrm{x}}}{\sqrt{1-{(1-{2\mathrm{e}}^{-\mathrm{x}})}^2}}\mathrm{dx}$$$$=\mathrm{y}\mathrm{arcos}(1-{2\mathrm{e}}^{-\mathrm{y}})+2{\int }_0^{\mathrm{y}}\frac{{\mathrm{xe}}^{-\mathrm{x}}}{\sqrt{1-{(1-{2\mathrm{e}}^{-\mathrm{x}})}^2}}\mathrm{dx}$$$$\mathrm{changement}1-{2\mathrm{e}}^{-\mathrm{x}}=\cos \alpha \mathrm{give}$$$${2\mathrm{e}}^{-\mathrm{x}}=1-\cos \alpha \Rightarrow {\mathrm{e}}^{-\mathrm{x}}=\frac{1-\cos \alpha }{2}\Rightarrow \mathrm{x}=-\ln \left(\frac{1-\cos \alpha }{2}\right)$$$$\Rightarrow \mathrm{dx}=-\frac{\sin \alpha }{1-\cos \alpha }\Rightarrow$$$${\int }_0^{\mathrm{y}}\frac{{\mathrm{xe}}^{-\mathrm{x}}}{\sqrt{1-{(1-{2\mathrm{e}}^{-\mathrm{x}})}^2}}\mathrm{dx}$$$$={\int }_{\pi }^{\mathrm{arcos}(1-{2\mathrm{e}}^{-\mathrm{y}})}-\ln \left(\frac{1-\cos \alpha }{2}\right)\times \frac{1-\cos \alpha }{2}\times (-\frac{\sin \alpha }{1-\cos \alpha })\times \frac{1}{\sin \alpha }\mathrm{d}\alpha$$$$=\frac{1}{2}{\int }_{\pi }^{\mathrm{arcos}(1-{2\mathrm{e}}^{-\mathrm{y}})}\ln \left(\frac{1-\cos \alpha }{2}\right)\mathrm{d}\alpha$$$$=\frac{1}{2}{\int }_{\pi }^{\mathrm{arcos}(1-{2\mathrm{e}}^{-\mathrm{y}})}2\ln \left(\cos \left(\frac{\alpha }{2}\right)\right)\mathrm{d}\alpha$$$${=}_{\frac{\alpha }{2}=\mathrm{t}}2{\int }_{\frac{\pi }{2}}^{\frac{1}{2}\mathrm{arcos}(1-{2\mathrm{e}}^{-\mathrm{y}})}\ln \left(\mathrm{cost}\right)\mathrm{dt}$$$$\to 2{\int }_{\frac{\pi }{2}}^0\ln \left(\mathrm{cost}\right)\mathrm{dt}=-2{\int }_0^{\frac{\pi }{2}}\ln \left(\mathrm{cost}\right)\mathrm{dt}=-2(-\frac{\pi }{2}\ln 2)$$$$=\pi \ln \left(2\right)\mathrm{also}\mathrm{yarcos}(1-{2\mathrm{e}}^{-\mathrm{y}})\to 0\Rightarrow$$$${\int }_0^{\mathrm{\infty }}\mathrm{arcos}(1-{2\mathrm{e}}^{-\mathrm{x}})\mathrm{dx}={\lim }_{\mathrm{y}\to +\mathrm{\infty }}\mathrm{A}\left(\mathrm{y}\right)=\pi \ln \left(2\right)$$$$$$$$$$

Commented by EmericGent last updated on 23/May/20

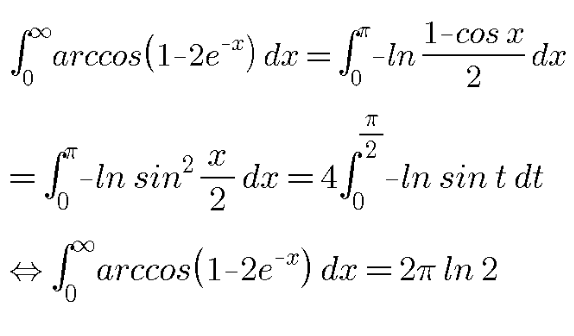
Commented by EmericGent last updated on 23/May/20

Actually you did a small mistake (forgot a *2 somewhere)

Commented by mathmax by abdo last updated on 24/May/20

$$\mathrm{error}\mathrm{at}\mathrm{final}\mathrm{line}\mathrm{we}\mathrm{have}{\int }_0^{\mathrm{y}}\frac{{\mathrm{xe}}^{-\mathrm{x}}}{\sqrt{1-{(1-{2\mathrm{e}}^{-\mathrm{x}})}^2}}\mathrm{dx}\to \pi \ln 2\mathrm{and}$$$$\mathrm{we}\mathrm{have}\mathrm{A}\left(\mathrm{y}\right)=\mathrm{y}\mathrm{arcos}(1-{2\mathrm{e}}^{-\mathrm{x}})+2{\int }_0^{\mathrm{y}}\frac{{\mathrm{xe}}^{-\mathrm{x}}}{\sqrt{1-{(1-{2\mathrm{e}}^{-\mathrm{x}})}^2}}\to 0+2\pi \ln 2$$$$\Rightarrow {\int }_0^{\mathrm{\infty }}\mathrm{arcos}(1-{2\mathrm{e}}^{-\mathrm{x}})\mathrm{dx}=2\pi \ln \left(2\right)$$

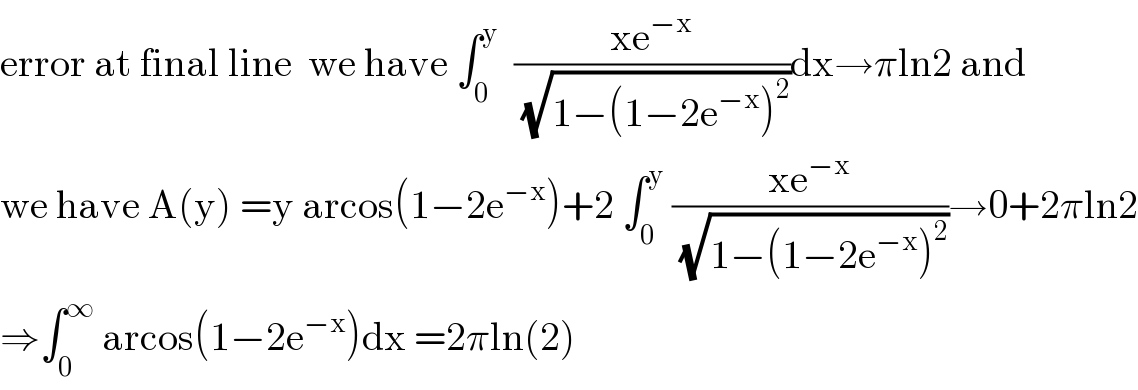
Answered by mathmax by abdo last updated on 24/May/20

$$\mathrm{I}={\int }_0^{\mathrm{\infty }}\mathrm{arcos}(1-{\mathrm{e}}^{-\mathrm{x}})\mathrm{dx}\mathrm{let}\mathrm{I}\left(\xi \right)={\int }_0^{\xi }\mathrm{arcos}(1-{\mathrm{e}}^{-\mathrm{x}})\mathrm{dx}\mathrm{by}\mathrm{parts}$$$$\mathrm{I}\left(\xi \right)={\left[\mathrm{x}\mathrm{arcos}(1-{\mathrm{e}}^{-\mathrm{x}})\right]}_0^{\xi }-{\int }_0^{\xi }\mathrm{x}(-\frac{{\mathrm{e}}^{-\mathrm{x}}}{\sqrt{1-{(1-{\mathrm{e}}^{-\mathrm{x}})}^2}})\mathrm{dx}$$$$=\xi \mathrm{arcos}(1-{\mathrm{e}}^{-\xi })+{\int }_0^{\xi }\frac{{\mathrm{xe}}^{-\mathrm{x}}}{\sqrt{1-{(1-{\mathrm{e}}^{-\mathrm{x}})}^2}}\mathrm{dx}$$$$\mathrm{changement}1-{\mathrm{e}}^{-\mathrm{x}}=\cos \alpha \mathrm{give}{\mathrm{e}}^{-\mathrm{x}}=1-\cos \alpha \Rightarrow \mathrm{x}=-\ln (1-\cos \alpha )$$$$\Rightarrow \frac{\mathrm{dx}}{\mathrm{d}\alpha }=-\frac{\sin \alpha }{1-\cos \alpha }\Rightarrow$$$${\int }_0^{\xi }\frac{{\mathrm{xe}}^{-\mathrm{x}}}{\sqrt{1-{(1-{\mathrm{e}}^{-\mathrm{x}})}^2}}\mathrm{dx}={\int }_{\frac{\pi }{2}}^{\mathrm{arcos}(1-{\mathrm{e}}^{-\xi })}\ln (1-\cos \alpha )\times (1-\cos \alpha )\times \frac{1}{\sin \alpha }\times \frac{\sin \alpha }{1-\cos \alpha }\mathrm{d}\alpha$$$$=-{\int }_{\mathrm{arcos}(1-{\mathrm{e}}^{-\xi })}^{\frac{\pi }{2}}\ln \left({2\sin }^2\left(\frac{\alpha }{2}\right)\right)\mathrm{d}\alpha$$$$=-\ln \left(2\right)(\frac{\pi }{2}-\mathrm{arcos}(1-{\mathrm{e}}^{-\xi }))-2{\int }_0^{\frac{\pi }{2}}\ln \left(\sin \left(\frac{\alpha }{2}\right)\right)\mathrm{d}\alpha (\frac{\alpha }{2}=\mathrm{u})$$$$=-\frac{\pi }{2}\ln \left(2\right)+\ln \left(2\right)\mathrm{arcos}(1-{\mathrm{e}}^{-\xi })-2{\int }_0^{\frac{\pi }{4}}\ln \left(\mathrm{u}\right)\left(2\mathrm{du}\right)$$$$=-\frac{\pi }{2}\ln \left(2\right)+\ln \left(2\right)\mathrm{arcos}(1-{\mathrm{e}}^{-\xi })-4{\int }_0^{\frac{\pi }{4}}\ln \left(\mathrm{u}\right)\mathrm{du}$$$$\to -\frac{\pi }{2}\ln \left(2\right)-4{\int }_0^{\frac{\pi }{4}}\ln \left(\mathrm{u}\right)\mathrm{du}\mathrm{rest}\mathrm{to}\mathrm{calculate}{\int }_0^{\frac{\pi }{4}}\ln \left(\mathrm{u}\right)\mathrm{du}..$$$$\mathrm{be}\mathrm{continued}...$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com