
Question and Answers Forum
Question Number 95106 by bobhans last updated on 23/May/20
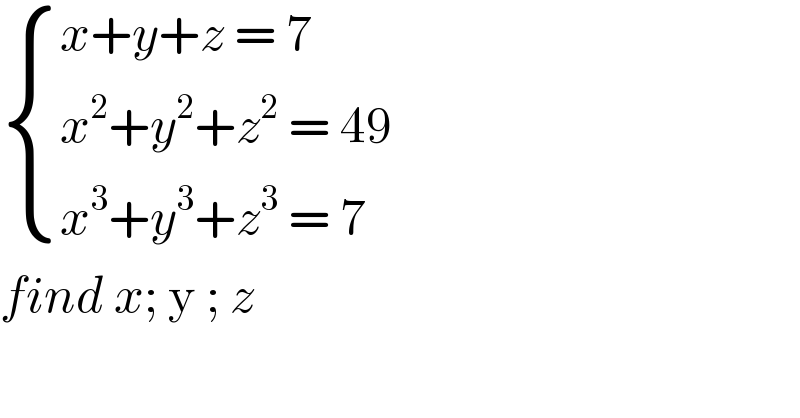
Answered by john santu last updated on 23/May/20
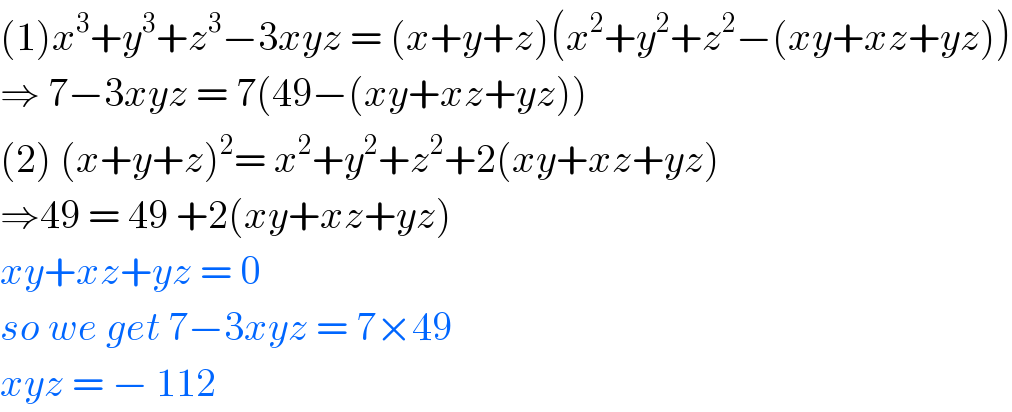
Commented by 1549442205 last updated on 23/May/20
![That is not fully answer!I have the following answer: We have 2(xy+yz+zx)=(x+y+z)^2 −(x^2 +y^2 +z^2 )=7^2 −49=0→xy+yz+zx=0→yz+ (y+z)x=0→yz+(7−x)x=0→yz=x^2 −7x(1) On the other hands,x^3 +y^3 +z^3 =7⇔ x^3 +[(y+z)^3 −3yz(y+z)]=7⇔x^3 +[(7−x)^3 − 3(x^2 −7x)(7−x)]=7⇔x^3 +[343−147x+ 21x^2 −x^3 −3(−x^3 +14x^2 −49x)]=7⇔ 3x^3 −21x^2 +336=0⇔x^3 −7x^2 +112=0. Putting x=(1/t) we get 112t^3 −7t+1=0.Multiplying two sides of the equation by 196=7^2 .4 and note 112= 7.4^2 then set u=28t we get PT: u^3 −49u+ 196=0(1) Put u=−(m+n)→u+m+n=0.Using the equality a^3 +b^3 +c^3 −3abc=(a+b+c)(a^2 + b^2 +c^2 −ab−bc−ca) we have u^3 +m^3 +n^3 − 3umn=0(2).From (1) and (2) we have: m^3 +n^3 =196(3),mn=((49)/3).It follows (m^3 −n^3 )^2 =(m^3 +n^3 )^2 −4(mn)^3 =196^2 − 4.(((49)/3))^3 =(((98)/9)(√(177)))^2 ⇒m^3 −n^3 =((98)/9)(√(177))(2) .Hence,from (1),(2)we get m^3 =( ((98(√(177)))/9)+196)/2 and n^3 =(196−((98(√(177)))/9))/2 ⇒u=−(m+n)= −[(^3 (√((1764+98(√(177)))/(18))) +^3 (√((1764−98(√(177)))/(18)))) Since u=28tand t=(1/x)⇒x=((28)/u)=−(1/7)[^3 (√((((1764+98(√(177)))/(18)))^2 ))−((49)/3)+^3 (√((((1764−98(√(177)))/(18)))^2 ))] Replace this value of x into the equations: x+y+z=7 and x(y+z)+yz=0 we find y,z which are image numbers](Q95113.png)
Commented by john santu last updated on 23/May/20
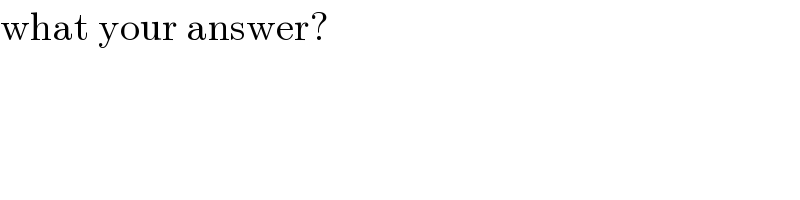
Commented by bobhans last updated on 23/May/20

Answered by mr W last updated on 23/May/20
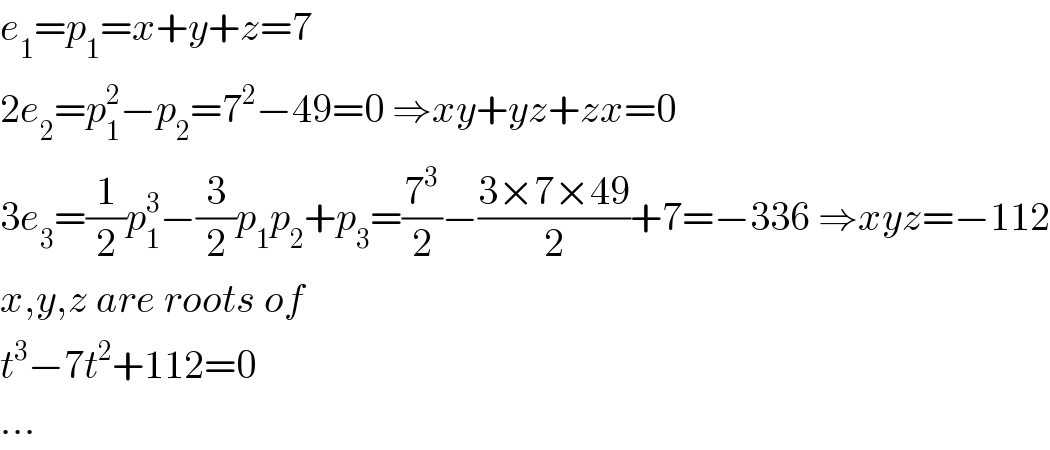
Commented by bobhans last updated on 23/May/20
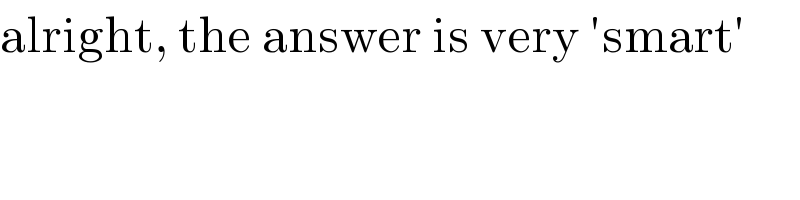
Commented by bobhans last updated on 23/May/20

Commented by mr W last updated on 23/May/20
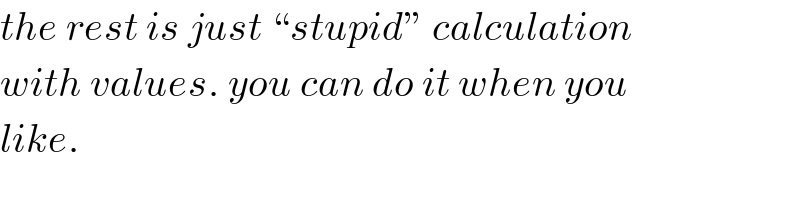
Commented by mr W last updated on 23/May/20
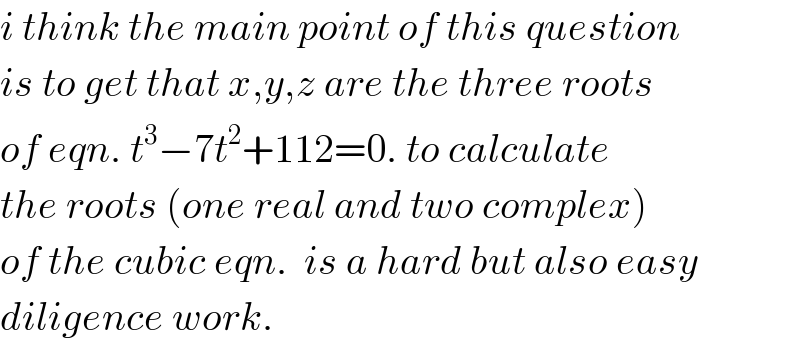
Commented by 1549442205 last updated on 23/May/20
![This equation has unique real root t=((−1)/7)[^3 (√((((1764+98(√(177)))/(18)))^2 ))−((49)/3)+^3 (√((((1764−98(√(177)))/(18)))^2 ))]like I done above.](Q95155.png)
