Solve the differential equations:− ★.(x sin x+cos x)(d^2 y/dx^2 ) −x cos x(dy/dx) + y cos x=0.


Question and Answers Forum

All Questions Topic List
Differential Equation Questions
Previous in All Question Next in All Question
Previous in Differential Equation Next in Differential Equation
Question Number 95119 by Mr.D.N. last updated on 27/May/20

$Solve the differential equations : -$ $★ . (x \sin x + \cos x) \frac{d^{2} y}{{dx}^{2}} - x \cos x \frac{dy}{dx} + y \cos x = 0 .$
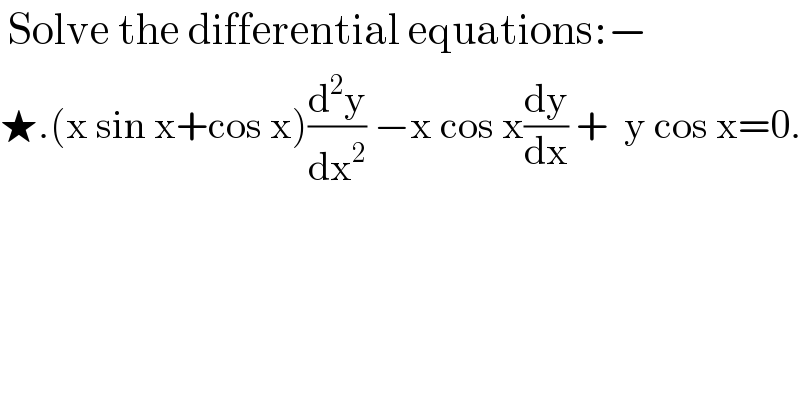
	Answered by niroj last updated on 23/May/20
	$2. (x sin x + cos x )(d^2 y/dx^2 ) − x cos x (dy/dx) + y cos x=0 Sol^n : (d^2 y/dx^2 ) − ((x cos x)/(x sin x+cos x)) (dy/dx) + ((cos x)/(x sin x+cos x)) y=0 We know the form of variable coefficient with constant If Part of CF is known,then we can use of special cases: (d^2 y/dx^2 )+P(dy/dx)+Qy =R.. Let, P= − ((x cos x)/(x sinx+ cos x)) Q= ((cos x)/(x sin x+cos x)) and R=0 ∴P+Qx=0 −((x cos x)/(x sin x+cos x)) + ((x cos x)/(x sin x+cos x))=0 If P+Qx=0, then part of CF u= x y=uv y=xv....(i) Special case: (d^2 v/dx^2 )+(p+(2/u)(du/dx))(dv/dx)=(R/u) (d^2 v/dx^2 )+(−((x cos x)/(x sin x+cos x)) + (2/x))(dv/dx)= (0/x) Put , (dv/dx)=t ⇒ (d^2 v/dx^2 )= (dt/dx) (dt/dx) +((2/x) − ((x cos x)/(x sinx+cos x)))t=0 IF= e^(∫ ((2/x) − ((x cos x)/(x sinx+ cos x)))dx) = e^((2log x −log (x sin x +cos x)) = e^(log x^2 ) .e^(log (x sin x +cos x)^(−1) ) = x^(2 ) . (1/(x sin x +cos x)) t. (x^2 /(x sin x+cos x)) = ∫ (x^2 /(x sinx+cos x)).0 dx+C_1 t (x^2 /(x sinx+cos x)) = C_1 t = ((x sin x+ cos x)/x^2 )C_1 (dv/dx) = ((x sin x+cos x)/x^2 )C_1 ∫ dv = C_1 ∫ ((xsin x+cos x)/x^2 )dx (x sin x+cos x)(d/dx) sinx+xcosx−sinx =xcos x ∫dv = C_1 [ (xsinx+cos x)∫(1/x^2 )−∫{(xsinx +cos x)(d/dx)∫(1/x^2 )dx}dx v= C_1 [ −(x sinx+cos x)(1/x) +∫xcos x(1/x)dx +C_2 v= C_1 [−(xsin x+cos x)(1/x)+sinx]+C_2 put value of v in eq^n (i) y= xv =C_1 [−x(x sinx+cos x)(1/x)+x sin x]+C_2 x = C_1 [ −xsinx −cos x+ x sinx]+C_2 x =− C_1 cos x+C_2 x ∴ y = −C_1 cos x+C_2 x ∴ y Whis is required differential equation.$
	$2 . (x \sin x + \cos x) \frac{d^{2} y}{{dx}^{2}} - x \cos x \frac{dy}{dx} + y \cos x = 0$ ${Sol}^{n} :$ $\frac{d^{2} y}{{dx}^{2}} - \frac{x \cos x}{x \sin x + \cos x} \frac{dy}{dx} + \frac{\cos x}{x \sin x + \cos x} y = 0$ $We know the form of variable coefficient with constant If Part of CF is$ $known, then we can use of special cases :$ $\frac{d^{2} y}{{dx}^{2}} + P \frac{dy}{dx} + Qy = R . .$ $Let, P = - \frac{x \cos x}{x sinx + \cos x}$ $Q = \frac{\cos x}{x \sin x + \cos x} and R = 0$ $∴ P + Qx = 0$ $- \frac{x \cos x}{x \sin x + \cos x} + \frac{x \cos x}{x \sin x + \cos x} = 0$ $If P + Qx = 0, then part of CF u = x$ $y = uv$ $y = xv . . . . (i)$ $Special case : \frac{d^{2} v}{{dx}^{2}} + (p + \frac{2}{u} \frac{du}{dx}) \frac{dv}{dx} = \frac{R}{u}$ $\frac{d^{2} v}{{dx}^{2}} + (- \frac{x \cos x}{x \sin x + \cos x} + \frac{2}{x}) \frac{dv}{dx} = \frac{0}{x}$ $Put, \frac{dv}{dx} = t \Rightarrow \frac{d^{2} v}{{dx}^{2}} = \frac{dt}{dx}$ $\frac{dt}{dx} + (\frac{2}{x} - \frac{x \cos x}{x sinx + \cos x}) t = 0$ $IF = e^{\int (\frac{2}{x} - \frac{x \cos x}{x sinx + \cos x}) dx}$ $= e^{(2 \log x - \log (x \sin x + \cos x)}$ $= e^{\log x^{2}} . e^{\log {(x \sin x + \cos x)}^{- 1}}$ $= x^{2} . \frac{1}{x \sin x + \cos x}$ $t . \frac{x^{2}}{x \sin x + \cos x} = \int \frac{x^{2}}{x sinx + \cos x} . 0 dx + C_{1}$ $t \frac{x^{2}}{x sinx + \cos x} = C_{1}$ $t = \frac{x \sin x + \cos x}{x^{2}} C_{1}$ $\frac{dv}{dx} = \frac{x \sin x + \cos x}{x^{2}} C_{1}$ $\int dv = C_{1} \int \frac{xsin x + \cos x}{x^{2}} dx$ $(x \sin x + \cos x) \frac{d}{dx}$ $sinx + xcosx - sinx = xcos x$ $\int dv = C_{1} [(xsinx + \cos x) \int \frac{1}{x^{2}} - \int {(xsinx + \cos x) \frac{d}{dx} \int \frac{1}{x^{2}} dx} dx$ $v = C_{1} [- (x sinx + \cos x) \frac{1}{x} + \int xcos x \frac{1}{x} dx + C_{2}$ $v = C_{1} [- (xsin x + \cos x) \frac{1}{x} + sinx] + C_{2}$ $put value of v in {eq}^{n} (i)$ $y = xv$ $= C_{1} [- x (x sinx + \cos x) \frac{1}{x} + x \sin x] + C_{2} x$ $= C_{1} [- xsinx - \cos x + x sinx] + C_{2} x$ $= - C_{1} \cos x + C_{2} x$ $∴ y = - C_{1} \cos x + C_{2} x$ $∴ y Whis is required differential equation .$
	Commented by Mr.D.N. last updated on 23/May/20
	outstanding aspect ��
	Commented by i jagooll last updated on 23/May/20
	coll man. ��
	Commented by niroj last updated on 23/May/20
	��
	Commented by peter frank last updated on 24/May/20

	$thank you$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum