Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 95401 by john santu last updated on 25/May/20

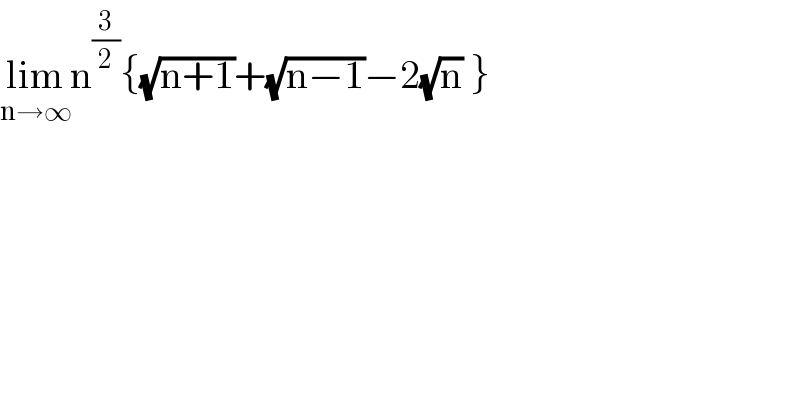
lim_(n→∞) n^(3/2) {(√(n+1))+(√(n−1))−2(√n) }

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}n}^{\frac{\mathrm{3}}{\mathrm{2}}} \left\{\sqrt{\mathrm{n}+\mathrm{1}}+\sqrt{\mathrm{n}−\mathrm{1}}−\mathrm{2}\sqrt{\mathrm{n}}\:\right\}\: \\ $$

Answered by john santu last updated on 25/May/20

Commented by bobhans last updated on 25/May/20

great

$$\mathrm{great} \\ $$

Answered by abdomathmax last updated on 25/May/20

let U_n =n^(3/2) {(√(n+1))+(√(n−1))−2(√n)} ⇒ U_n =n^(3/2) {(√n)(√(1+(1/n)))+(√n)(√(1−(1/n)))−2(√n)} but (√(1+(1/n)))=(1+(1/n))^(1/2) ∼1+(1/(2n)) +(((1/2)((1/2)−1))/(2n^2 )) =1+(1/(2n))−(1/(8n^2 )) and (√(1−(1/n)))=1−(1/(2n))−(1/(8n^2 )) ⇒ (√(n+1))+(√(n−1))−2(√n)∼(√n)+(1/(2(√n)))−((√n)/(8n^2 )) +(√n)−(1/(2(√n)))−((√n)/(8n^2 )) −2(√n) =−((√n)/(4n^2 )) =−(1/4) n^((1/2)−2) =−(1/4)n^(−(3/2)) ⇒ U_n ∼n^(3/2) ×(−(1/4))n^(−(3/2)) ⇒U_n ∼−(1/4) ⇒ lim_(n→+∞) U_n =−(1/4)

$$\mathrm{let}\:\mathrm{U}_{\mathrm{n}} =\mathrm{n}^{\frac{\mathrm{3}}{\mathrm{2}}} \left\{\sqrt{\mathrm{n}+\mathrm{1}}+\sqrt{\mathrm{n}−\mathrm{1}}−\mathrm{2}\sqrt{\mathrm{n}}\right\}\:\Rightarrow \\ $$$$\mathrm{U}_{\mathrm{n}} =\mathrm{n}^{\frac{\mathrm{3}}{\mathrm{2}}} \left\{\sqrt{\mathrm{n}}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}}+\sqrt{\mathrm{n}}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}}}−\mathrm{2}\sqrt{\mathrm{n}}\right\}\:\mathrm{but} \\ $$$$\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}}=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\sim\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}}\:+\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2n}^{\mathrm{2}} } \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}}−\frac{\mathrm{1}}{\mathrm{8n}^{\mathrm{2}} }\:\:\mathrm{and} \\ $$$$\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2n}}−\frac{\mathrm{1}}{\mathrm{8n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sqrt{\mathrm{n}+\mathrm{1}}+\sqrt{\mathrm{n}−\mathrm{1}}−\mathrm{2}\sqrt{\mathrm{n}}\sim\sqrt{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{n}}}−\frac{\sqrt{\mathrm{n}}}{\mathrm{8n}^{\mathrm{2}} } \\ $$$$+\sqrt{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{n}}}−\frac{\sqrt{\mathrm{n}}}{\mathrm{8n}^{\mathrm{2}} }\:−\mathrm{2}\sqrt{\mathrm{n}} \\ $$$$=−\frac{\sqrt{\mathrm{n}}}{\mathrm{4n}^{\mathrm{2}} }\:=−\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{n}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}} \:=−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{n}^{−\frac{\mathrm{3}}{\mathrm{2}}} \:\Rightarrow \\ $$$$\mathrm{U}_{\mathrm{n}} \sim\mathrm{n}^{\frac{\mathrm{3}}{\mathrm{2}}} ×\left(−\frac{\mathrm{1}}{\mathrm{4}}\right)\mathrm{n}^{−\frac{\mathrm{3}}{\mathrm{2}}} \:\Rightarrow\mathrm{U}_{\mathrm{n}} \sim−\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{U}_{\mathrm{n}} =−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$

Commented by i jagooll last updated on 25/May/20

binomial series ?

$$\mathrm{binomial}\:\mathrm{series}\:? \\ $$

Commented by abdomathmax last updated on 25/May/20

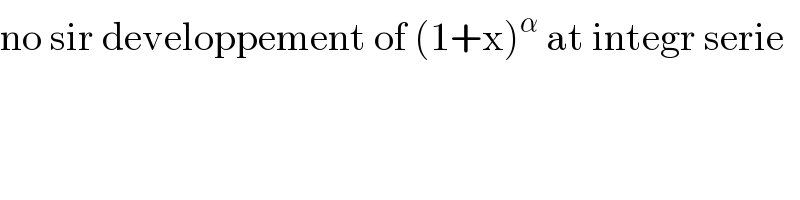
no sir developpement of (1+x)^α at integr serie

$$\mathrm{no}\:\mathrm{sir}\:\mathrm{developpement}\:\mathrm{of}\:\left(\mathrm{1}+\mathrm{x}\right)^{\alpha} \:\mathrm{at}\:\mathrm{integr}\:\mathrm{serie} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com