
Question and Answers Forum
Question Number 95547 by Fikret last updated on 25/May/20
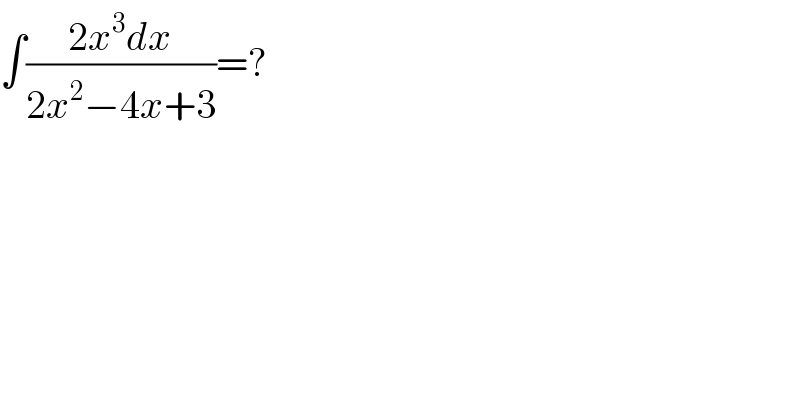
Answered by MJS last updated on 25/May/20
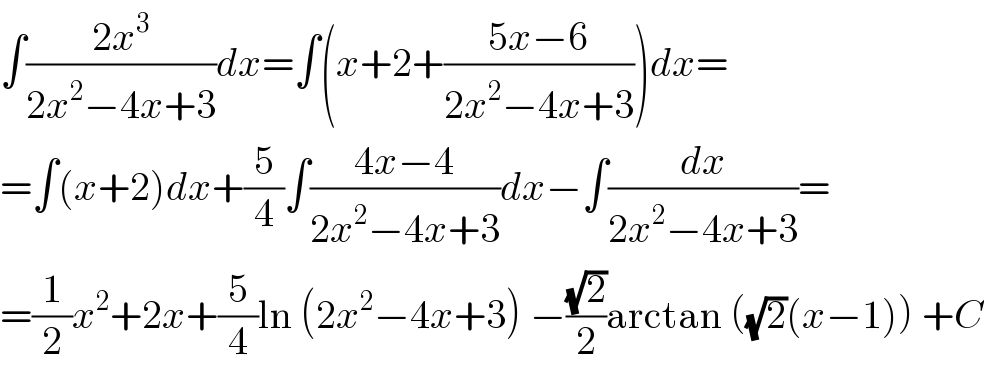
Commented by peter frank last updated on 26/May/20

Answered by 1549442205 last updated on 26/May/20
![we have ((2x^3 )/(2x^2 −4x+3))=x+2+((5x−6)/(2x^2 −4x+3)) x+2+((5(x−1)−1)/(2x^2 −4x+3)) x+2+(((5/4)(4x−4)−1)/(2x^2 −4x+3))=x+2+(((5/4)(4x−4))/(2x^2 −4x+3)) −(1/(2x^2 −4x+3)).Hence,denoting I the integral above we have: I=(x^2 /2)+2x+(5/4)ln(2x^2 −4x+3)−∫(dx/(2x^2 −4x+3)) J=∫(dx/(2x^2 −4x+3))=(1/2)∫(dx/((x−1)^2 +(((√2)/(2))))^2 )) =(√2)tan^(−1) [(√2)(x−1)]+C.Thus, I=(x^2 /2)+2x+(5/4)ln(2x^2 −4x+3)−((√2)/2)tan^(−1) [(√2)(x−1)]+C](Q95566.png)
| ||
Question and Answers Forum | ||
Question Number 95547 by Fikret last updated on 25/May/20 | ||
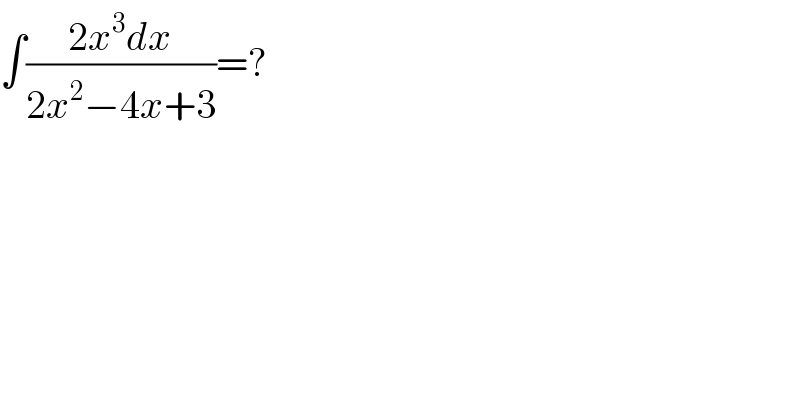 | ||
Answered by MJS last updated on 25/May/20 | ||
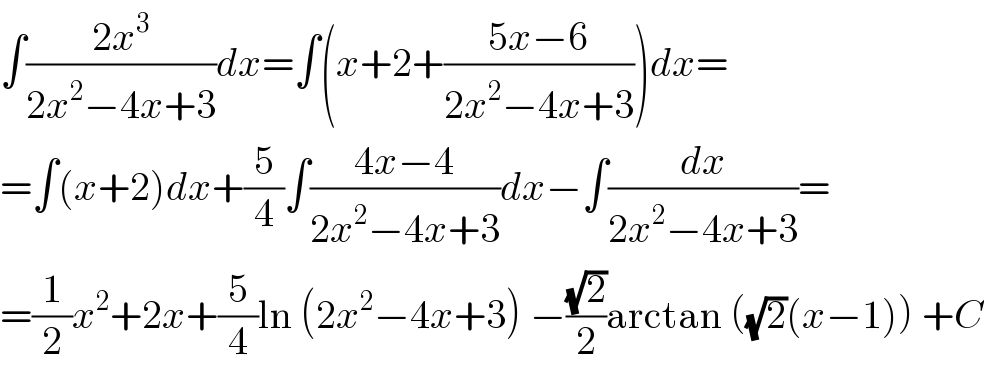 | ||
| ||
Commented by peter frank last updated on 26/May/20 | ||
 | ||
Answered by 1549442205 last updated on 26/May/20 | ||
![we have ((2x^3 )/(2x^2 −4x+3))=x+2+((5x−6)/(2x^2 −4x+3)) x+2+((5(x−1)−1)/(2x^2 −4x+3)) x+2+(((5/4)(4x−4)−1)/(2x^2 −4x+3))=x+2+(((5/4)(4x−4))/(2x^2 −4x+3)) −(1/(2x^2 −4x+3)).Hence,denoting I the integral above we have: I=(x^2 /2)+2x+(5/4)ln(2x^2 −4x+3)−∫(dx/(2x^2 −4x+3)) J=∫(dx/(2x^2 −4x+3))=(1/2)∫(dx/((x−1)^2 +(((√2)/(2))))^2 )) =(√2)tan^(−1) [(√2)(x−1)]+C.Thus, I=(x^2 /2)+2x+(5/4)ln(2x^2 −4x+3)−((√2)/2)tan^(−1) [(√2)(x−1)]+C](Q95566.png) | ||
| ||