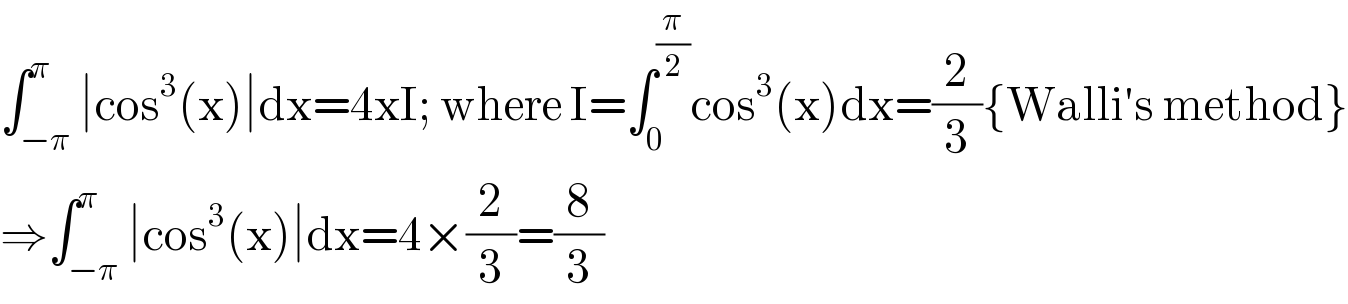Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 95549 by Fikret last updated on 25/May/20

∫_(−π) ^π ∣cos^3 x∣dx

$$\int_{−\pi} ^{\pi} \mid{cos}^{\mathrm{3}} {x}\mid{dx} \\ $$

Answered by MJS last updated on 26/May/20

∫_(−π) ^π ∣cos^3 x∣dx=4∫_0 ^(π/2) cos^3 x dx= =∫_0 ^(π/2) (cos 3x +3cos x)dx= =[(1/3)sin 3x +3sin x]_0 ^(π/2) =(8/3)

$$\underset{−\pi} {\overset{\pi} {\int}}\mid\mathrm{cos}^{\mathrm{3}} \:{x}\mid{dx}=\mathrm{4}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{cos}^{\mathrm{3}} \:{x}\:{dx}= \\ $$$$=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\left(\mathrm{cos}\:\mathrm{3}{x}\:+\mathrm{3cos}\:{x}\right){dx}= \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}\:\mathrm{3}{x}\:+\mathrm{3sin}\:{x}\right]_{\mathrm{0}} ^{\pi/\mathrm{2}} =\frac{\mathrm{8}}{\mathrm{3}} \\ $$

Commented by peter frank last updated on 26/May/20

why you change limit sir

$$\mathrm{why}\:\mathrm{you}\:\mathrm{change}\:\mathrm{limit}\:\mathrm{sir} \\ $$

Commented by MJS last updated on 26/May/20

because ∣cos^3 x∣ is periodic... scetch it

$$\mathrm{because}\:\mid\mathrm{cos}^{\mathrm{3}} \:{x}\mid\:\mathrm{is}\:\mathrm{periodic}...\:\mathrm{scetch}\:\mathrm{it} \\ $$

Commented by peter frank last updated on 26/May/20

how abou this ∫_(−π) ^π ∣sin x∣ dx ?

$$\mathrm{how}\:\mathrm{abou}\:\mathrm{this} \\ $$$$\int_{−\pi} ^{\pi} \mid\mathrm{sin}\:\mathrm{x}\mid\:\mathrm{dx}\:? \\ $$

Commented by MJS last updated on 26/May/20

∫_(−π) ^π ∣sin x∣dx=4∫_0 ^(π/2) sin x dx the idea is to get rid of the absolute by finding an interval where the function is greater than or equal to zero

$$\underset{−\pi} {\overset{\pi} {\int}}\mid\mathrm{sin}\:{x}\mid{dx}=\mathrm{4}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{sin}\:{x}\:{dx} \\ $$$$\mathrm{the}\:\mathrm{idea}\:\mathrm{is}\:\mathrm{to}\:\mathrm{get}\:\mathrm{rid}\:\mathrm{of}\:\mathrm{the}\:\mathrm{absolute}\:\mathrm{by} \\ $$$$\mathrm{finding}\:\mathrm{an}\:\mathrm{interval}\:\mathrm{where}\:\mathrm{the}\:\mathrm{function}\:\mathrm{is} \\ $$$$\mathrm{greater}\:\mathrm{than}\:\mathrm{or}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{zero} \\ $$

Commented by peter frank last updated on 26/May/20

thank you

$$\mathrm{thank}\:\mathrm{you}\: \\ $$

Answered by 1549442205 last updated on 26/May/20

I=∫_(−Π) ^Π ∣cos^3 x∣dx=∫_(−Π) ^((−Π)/2) (−cos^3 x)dx +∫_(−(Π/2)) ^(Π/2) cos^3 xdx+∫_(Π/2) ^Π (−cos^3 x)dx We have F(x)=∫cos^3 xdx=∫(1−sin^2 x)dsinx =sinx−((sin^3 x)/3)+C.Therefore, I=F(−Π)−F(((−Π)/2))+F((Π/2))−F(((−Π)/2)) +F((Π/2))−F(Π)=2F((Π/2))−2F(((−Π)/2)) =(4/3)−2(((−2)/3))=(8/3)(Since F(Π)=F(−Π)=0 .Thus,I=(8/3)

$$\mathrm{I}=\int_{−\Pi} ^{\Pi} \mid\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}\mid\mathrm{dx}=\int_{−\Pi} ^{\frac{−\Pi}{\mathrm{2}}} \left(−\mathrm{cos}^{\mathrm{3}} \mathrm{x}\right)\mathrm{dx} \\ $$$$+\int_{−\frac{\Pi}{\mathrm{2}}} ^{\frac{\Pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{3}} \mathrm{xdx}+\int_{\frac{\Pi}{\mathrm{2}}} ^{\Pi} \left(−\mathrm{cos}^{\mathrm{3}} \mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{F}\left(\mathrm{x}\right)=\int\mathrm{cos}^{\mathrm{3}} \mathrm{xdx}=\int\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dsinx} \\ $$$$=\mathrm{sinx}−\frac{\mathrm{sin}^{\mathrm{3}} \mathrm{x}}{\mathrm{3}}+\mathrm{C}.\mathrm{Therefore}, \\ $$$$\mathrm{I}=\mathrm{F}\left(−\Pi\right)−\mathrm{F}\left(\frac{−\Pi}{\mathrm{2}}\right)+\mathrm{F}\left(\frac{\Pi}{\mathrm{2}}\right)−\mathrm{F}\left(\frac{−\Pi}{\mathrm{2}}\right) \\ $$$$+\mathrm{F}\left(\frac{\Pi}{\mathrm{2}}\right)−\mathrm{F}\left(\Pi\right)=\mathrm{2F}\left(\frac{\Pi}{\mathrm{2}}\right)−\mathrm{2F}\left(\frac{−\Pi}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{2}\left(\frac{−\mathrm{2}}{\mathrm{3}}\right)=\frac{\mathrm{8}}{\mathrm{3}}\left(\mathrm{Since}\:\mathrm{F}\left(\Pi\right)=\mathrm{F}\left(−\Pi\right)=\mathrm{0}\right. \\ $$$$.\mathrm{Thus},\mathrm{I}=\frac{\mathrm{8}}{\mathrm{3}} \\ $$

Answered by Ar Brandon last updated on 26/May/20

∫_(−π) ^π ∣cos^3 (x)∣dx=4xI; where I=∫_0 ^(π/2) cos^3 (x)dx=(2/3){Walli′s method} ⇒∫_(−π) ^π ∣cos^3 (x)∣dx=4×(2/3)=(8/3)

$$\int_{−\pi} ^{\pi} \mid\mathrm{cos}^{\mathrm{3}} \left(\mathrm{x}\right)\mid\mathrm{dx}=\mathrm{4xI};\:\mathrm{where}\:\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{3}} \left(\mathrm{x}\right)\mathrm{dx}=\frac{\mathrm{2}}{\mathrm{3}}\left\{\mathrm{Walli}'\mathrm{s}\:\mathrm{method}\right\} \\ $$$$\Rightarrow\int_{−\pi} ^{\pi} \mid\mathrm{cos}^{\mathrm{3}} \left(\mathrm{x}\right)\mid\mathrm{dx}=\mathrm{4}×\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{8}}{\mathrm{3}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com