
Question and Answers Forum
Question Number 95585 by turbo msup by abdo last updated on 26/May/20
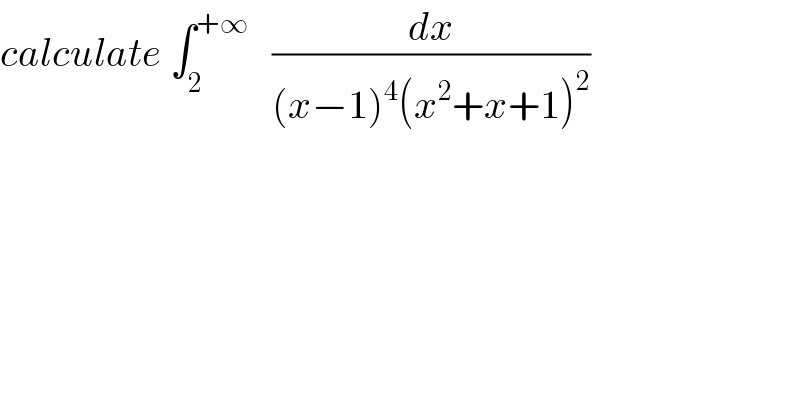
Answered by MJS last updated on 26/May/20
![∫(dx/((x−1)^4 (x^2 +x+1)^2 ))= [Ostrogradski] =−((8x^4 −11x^3 −2x^2 −x+9)/(27(x−1)^4 (x^2 +x+1)))−(2/(27))∫((4x+5)/((x−1)(x^2 +x+1)))dx −(2/(27))∫((4x+5)/((x−1)(x^2 +x+1)))dx= =(2/(27))∫((3x+2)/(x^2 +x+1))dx−(2/9)∫(dx/(x−1))= =((2(√3))/(81))arctan (((√3)(2x+1))/3) +(1/9)ln (x^2 +x+1) −(2/9)ln (x−1) = =((2(√3))/(81))arctan (((√3)(2x+1))/3) +(1/9)ln ((x^2 +x+1)/((x−1)^2 )) +C ⇒ ∫_2 ^(+∞) (dx/((x−1)^4 (x^2 +x+1)^2 ))= =((13)/(63))+((π(√3))/(81))−((ln 7)/9)−((2(√3))/(81))arctan ((5(√3))/3)](Q95621.png)
Commented by mathmax by abdo last updated on 27/May/20

| ||
Question and Answers Forum | ||
Question Number 95585 by turbo msup by abdo last updated on 26/May/20 | ||
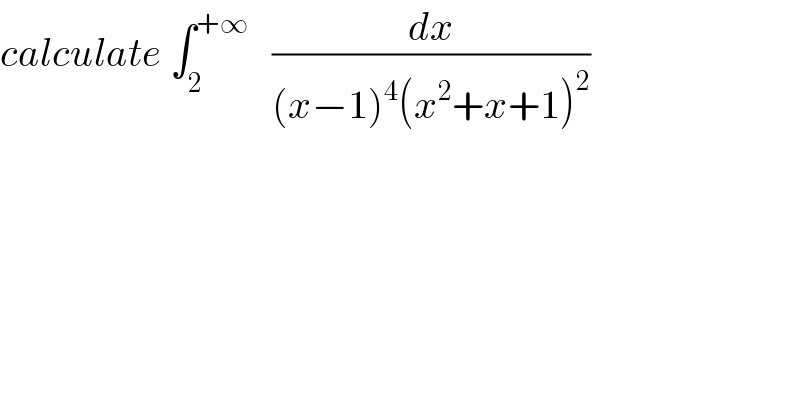 | ||
Answered by MJS last updated on 26/May/20 | ||
![∫(dx/((x−1)^4 (x^2 +x+1)^2 ))= [Ostrogradski] =−((8x^4 −11x^3 −2x^2 −x+9)/(27(x−1)^4 (x^2 +x+1)))−(2/(27))∫((4x+5)/((x−1)(x^2 +x+1)))dx −(2/(27))∫((4x+5)/((x−1)(x^2 +x+1)))dx= =(2/(27))∫((3x+2)/(x^2 +x+1))dx−(2/9)∫(dx/(x−1))= =((2(√3))/(81))arctan (((√3)(2x+1))/3) +(1/9)ln (x^2 +x+1) −(2/9)ln (x−1) = =((2(√3))/(81))arctan (((√3)(2x+1))/3) +(1/9)ln ((x^2 +x+1)/((x−1)^2 )) +C ⇒ ∫_2 ^(+∞) (dx/((x−1)^4 (x^2 +x+1)^2 ))= =((13)/(63))+((π(√3))/(81))−((ln 7)/9)−((2(√3))/(81))arctan ((5(√3))/3)](Q95621.png) | ||
| ||
Commented by mathmax by abdo last updated on 27/May/20 | ||
 | ||