Previous in Differential Equation Next in Differential Equation
Question Number 95677 by Rio Michael last updated on 26/May/20
$$\:\mathrm{Given}\:{f}\left({x}\right)\:=\:\frac{\mathrm{ln}\:{x}}{{x}−\mathrm{1}} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{find}\:\mathrm{the}\:\mathrm{domain}\:\mathrm{of}\:{f}. \\ $$$$\left(\mathrm{b}\right)\:\mathrm{find}\:\mathrm{the}\:\mathrm{limts}\:\mathrm{of}\:{f}\:\mathrm{at}\:\mathrm{the}\:\mathrm{boundary}\:\mathrm{of}\:\mathrm{its}\:\mathrm{domain} \\ $$$$\mathrm{hence}\:\mathrm{state}\:\mathrm{the}\:\mathrm{asymptote}\:\mathrm{of}\:{y}\:=\:{f}\left({x}\right). \\ $$
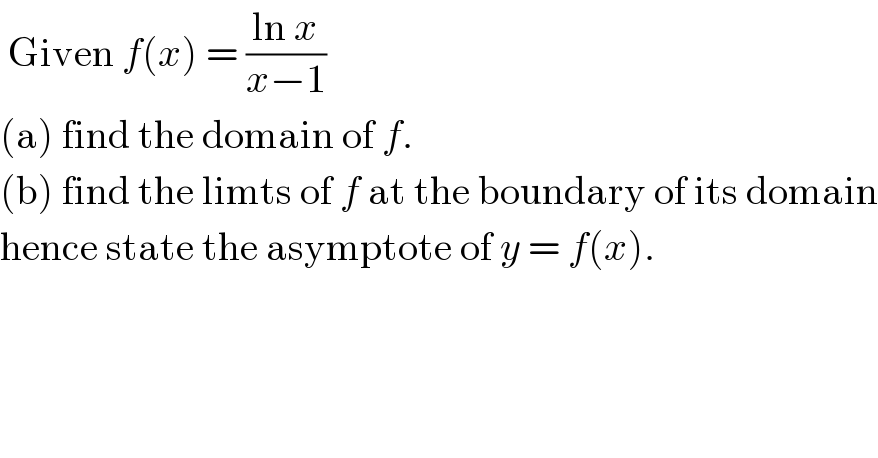
Answered by mathmax by abdo last updated on 27/May/20
![1)D_f =]0,1[∪]1,+∞[ 2)lim_(x→o^+ ) f(x) =+∞ and lim_(x→1^+ ) f(x)=lim_(x→1) f(x) =1 lim_(x→+∞) f(x) =lim_(x→+∞) ((lnx)/(x(1−x^(−1) ))) =lim_(x→+∞) ((lnx)/x)=0 ⇒ y=0 is assymtote for C_f](Q95685.png)
$$\left.\mathrm{1}\left.\right)\mathrm{D}_{\mathrm{f}} =\right]\mathrm{0},\mathrm{1}\left[\cup\right]\mathrm{1},+\infty\left[\right. \\ $$$$\left.\mathrm{2}\right)\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{o}^{+} } \:\:\mathrm{f}\left(\mathrm{x}\right)\:=+\infty\:\:\:\mathrm{and}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}^{+} } \mathrm{f}\left(\mathrm{x}\right)=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{1} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\:\frac{\mathrm{lnx}}{\mathrm{x}\left(\mathrm{1}−\mathrm{x}^{−\mathrm{1}} \right)}\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\:\frac{\mathrm{lnx}}{\mathrm{x}}=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{y}=\mathrm{0}\:\mathrm{is}\:\mathrm{assymtote}\:\mathrm{for}\:\mathrm{C}_{\mathrm{f}} \\ $$
Commented by Rio Michael last updated on 27/May/20
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir}. \\ $$