
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 95695 by mathmax by abdo last updated on 27/May/20
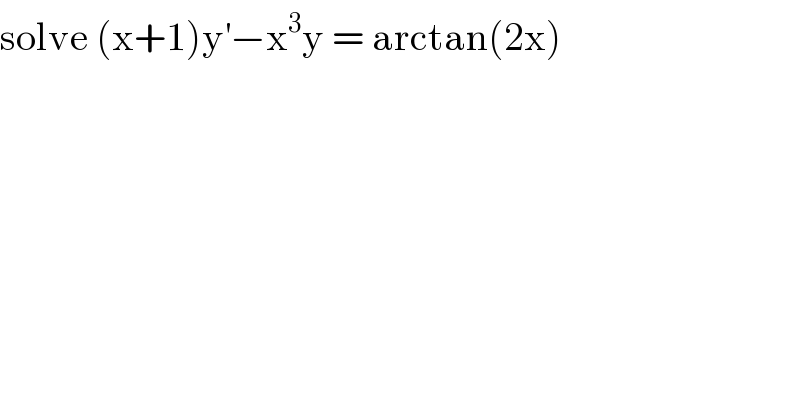
Answered by mathmax by abdo last updated on 27/May/20
![(he) ⇒(x+1)y^′ −x^3 y =0 ⇒(y^′ /y) =(x^3 /(x+1)) ⇒ln∣y∣ =∫(x^3 /(x+1)) dx +c =∫ ((x^3 +1−1)/(x+1))dx+c =∫ ((x^3 +1)/(x+1))dx −∫ (dx/(x+1))+c =∫(x^2 −x+1)dx−ln∣x+1∣ +c =(x^3 /3)−(x^2 /2) +x−ln∣x+1 ∣ +c ⇒y =(k/(∣x+1∣)) e^((x^3 /3)−(x^2 /2)+x) let find the solution on ]−1,+∞[ ⇒y =(k/(x+1))e^((x^3 /3)−(x^2 /2)+x) mvc method → y^′ =(k^′ /(x+1))e^((x^3 /3)−(x^2 /2)+x) +k(−(1/((x+1)^2 ))e^((x^3 /3)−(x^2 /2)+x) +(1/(x+1))×(x^2 −x+1)e^((x^3 /3)−(x^2 /2)+x) ) (e)⇒k^′ e^((x^3 /3)−(x^2 /2)+x) −(k/((x+1)))e^((x^3 /3)−(x^2 /2)+x) +k(x^2 −x+1) e^((x^3 /3)−(x^2 /2)+x) −((kx^3 )/(x+1)) e^((x^3 /3)−(x^2 /2)+x) =arctan(2x) ⇒k^′ =arctan(2x) e^(−(x^3 /3)−(x^2 /2)+x) ⇒k(x) =∫_. ^x arctan(2u)e^(−(u^3 /3)−(u^2 /2)+u) du +c ⇒ y(x) =(1/(x+1))e^((x^3 /3)−(x^2 /2)+x) ( ∫_. ^x arctan(2u)e^(−(u^3 /3)−(u^2 /2)+u) du +c) =(c/(x+1)) e^((x^3 /3)−(x^2 /2)+x) +(1/(x+1))e^((x^3 /3)−(x^2 /2)+x) ∫_. ^x arctan(2u)e^(−(u^3 /3)−(u^2 /2)+u) du](Q95762.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 95695 by mathmax by abdo last updated on 27/May/20 | ||
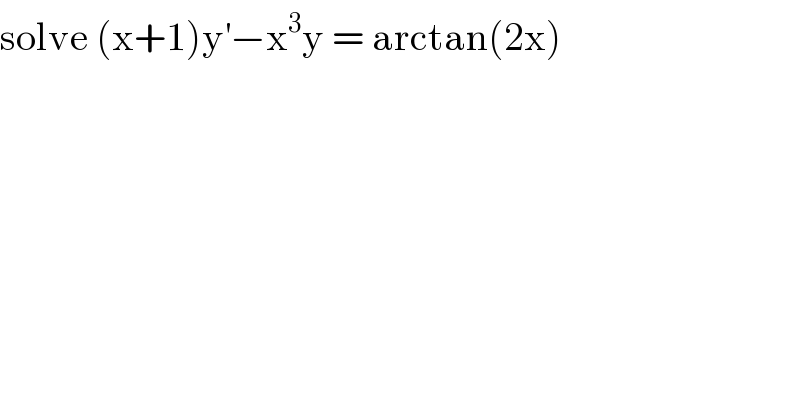 | ||
Answered by mathmax by abdo last updated on 27/May/20 | ||
![(he) ⇒(x+1)y^′ −x^3 y =0 ⇒(y^′ /y) =(x^3 /(x+1)) ⇒ln∣y∣ =∫(x^3 /(x+1)) dx +c =∫ ((x^3 +1−1)/(x+1))dx+c =∫ ((x^3 +1)/(x+1))dx −∫ (dx/(x+1))+c =∫(x^2 −x+1)dx−ln∣x+1∣ +c =(x^3 /3)−(x^2 /2) +x−ln∣x+1 ∣ +c ⇒y =(k/(∣x+1∣)) e^((x^3 /3)−(x^2 /2)+x) let find the solution on ]−1,+∞[ ⇒y =(k/(x+1))e^((x^3 /3)−(x^2 /2)+x) mvc method → y^′ =(k^′ /(x+1))e^((x^3 /3)−(x^2 /2)+x) +k(−(1/((x+1)^2 ))e^((x^3 /3)−(x^2 /2)+x) +(1/(x+1))×(x^2 −x+1)e^((x^3 /3)−(x^2 /2)+x) ) (e)⇒k^′ e^((x^3 /3)−(x^2 /2)+x) −(k/((x+1)))e^((x^3 /3)−(x^2 /2)+x) +k(x^2 −x+1) e^((x^3 /3)−(x^2 /2)+x) −((kx^3 )/(x+1)) e^((x^3 /3)−(x^2 /2)+x) =arctan(2x) ⇒k^′ =arctan(2x) e^(−(x^3 /3)−(x^2 /2)+x) ⇒k(x) =∫_. ^x arctan(2u)e^(−(u^3 /3)−(u^2 /2)+u) du +c ⇒ y(x) =(1/(x+1))e^((x^3 /3)−(x^2 /2)+x) ( ∫_. ^x arctan(2u)e^(−(u^3 /3)−(u^2 /2)+u) du +c) =(c/(x+1)) e^((x^3 /3)−(x^2 /2)+x) +(1/(x+1))e^((x^3 /3)−(x^2 /2)+x) ∫_. ^x arctan(2u)e^(−(u^3 /3)−(u^2 /2)+u) du](Q95762.png) | ||
| ||