Math Question and Answers


Question and Answers Forum

All Questions Topic List
Permutation and Combination Questions
Previous in All Question Next in All Question
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 95723 by i jagooll last updated on 27/May/20

Commented by bobhans last updated on 27/May/20
the case is ssma with there are 5 women 2 men sitting in 7 chairs with no 2 men sitting side by side
	Answered by Rio Michael last updated on 27/May/20

	$the 5 girls can stand in a row in 5! ways$ $let the girls be labeled as below$ $G_{1} G_{2} G_{3} G_{4} G_{5}$ $the first boy coming in has 6 vacancies$ $the second has 5 vacanciies$ $the third has 4 vacancies so$ $\Rightarrow number of ways = 5! \times 6 \times 5 \times 4 = 14 400 ways$
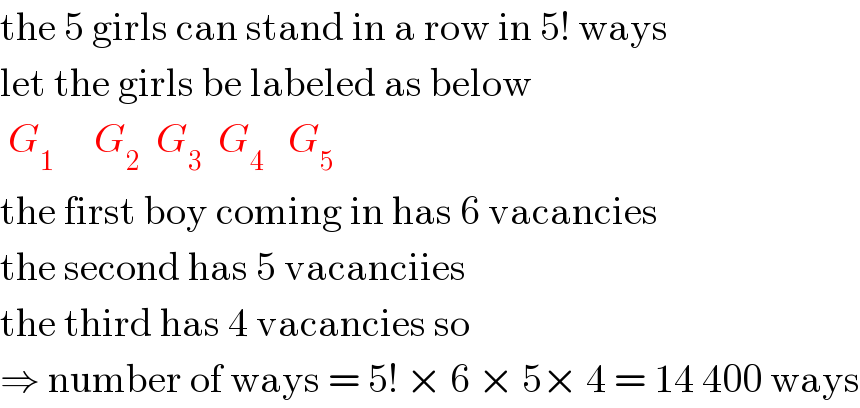
	Commented by mr W last updated on 27/May/20

	$14400 i s c o r r e c t! R i o M i c h a e l s i r :$ $w h e r e d o y o u t h i n k y o u a r e w r o n g ?$
	Commented by i jagooll last updated on 27/May/20

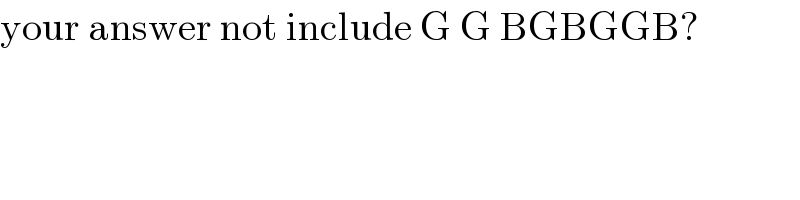
	$your answer not include G G BGBGGB ?$
	Commented by Rio Michael last updated on 28/May/20

	$well sir i was in a hurry on that problem$ $when the others dropped thier solution$ $i thought i misread it .$
	Answered by bobhans last updated on 27/May/20

	$totally arrangement = 8!$ $2 boy stand are together = C_{2}^{3} . 3! 6!$ $then = 8! - 6.6! = 6! \times 50$
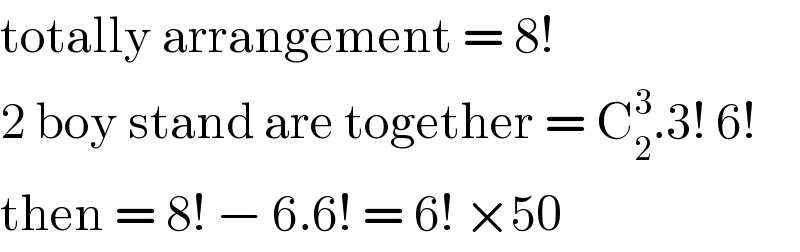
	Answered by mr W last updated on 27/May/20

	$M E T H O D I$ $b e t w e e n t w o b o y s t h e r e m u s t b e a t l e a s t$ $o n e g i r l .$ $w e a r r a n g e a t f i r s t t h e 5 g i r l s, t h e r e$ $a r e 5! w a y s .$ $◻ G ◻ G ◻ G ◻ G ◻ G ◻$ $t h e 3 b o y s c a n n o w t a k e t h r e e o f$ $6 p o s i t i o n s (◻) . t h e r e a r e C_{3}^{6} \times 3! w a y s .$ $s o t o t a l l y t h e r e a r e C_{3}^{6} \times 3! \times 5! = 14400$ $w a y s .$ $M E T H O D I I$ $t o a r r a n g e 8 c h i l d r e n t h e r e a r e 8!$ $w a y s .$ $t o a r r a n g e t h e m s u c h t h a t t h r e e b o y s$ $a r e t o g e t h e r, t h e r e a r e 6! \times 3! w a y s .$ $t o a r r a n g e t h e m s u c h t h a t t w o a n d$ $o n l y t w o b o y s a r e n e x t t o e a c h o t h e r,$ $t h e r e a r e C_{2}^{3} \times (7! - 2 \times 6!) \times 2! w a y s .$ $t o t a l v a l i d a r r a n g e m e n t s :$ $8! - C_{2}^{3} \times (7! - 2 \times 6!) \times 2! - 6! \times 3! = 14400$
	Commented by john santu last updated on 28/May/20

	$oo yes . . . your right . i^{'} m using method II$ $but forgot something . ok thanks you$
	Commented by bobhans last updated on 28/May/20

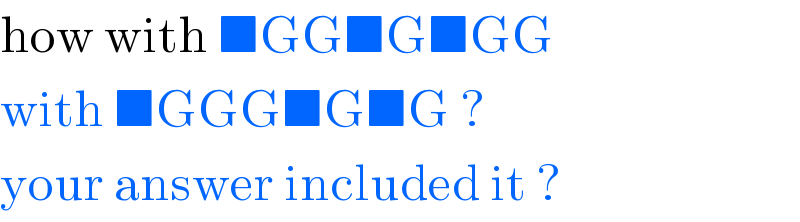
	$how with ◼ GG ◼ G ◼ GG$ $with ◼ GGG ◼ G ◼ G ?$ $your answer included it ?$
	Commented by mr W last updated on 28/May/20

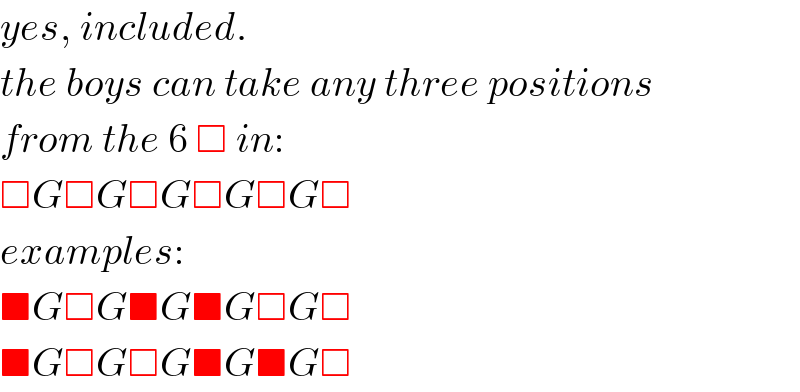
	$y e s, i n c l u d e d .$ $t h e b o y s c a n t a k e a n y t h r e e p o s i t i o n s$ $f r o m t h e 6 ◻ i n :$ $◻ G ◻ G ◻ G ◻ G ◻ G ◻$ $e x a m p l e s :$ $◼ G ◻ G ◼ G ◼ G ◻ G ◻$ $◼ G ◻ G ◻ G ◼ G ◼ G ◻$
	Commented by i jagooll last updated on 28/May/20

	$thank you sir$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum