Previous in Relation and Functions Next in Relation and Functions
Question Number 95839 by mathmax by abdo last updated on 28/May/20
$$\mathrm{solve}\:\mathrm{y}^{\left(\mathrm{3}\right)} −\mathrm{2y}^{\left(\mathrm{2}\right)} \:+\mathrm{3y}\:\:−\mathrm{2y}\:=\mathrm{sinx} \\ $$
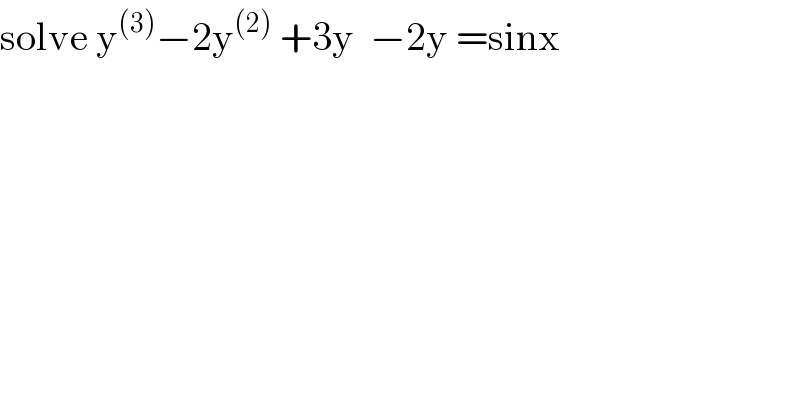
Commented by john santu last updated on 28/May/20
$$\mathrm{homogenous}\:\mathrm{solution} \\ $$$$\lambda^{\mathrm{3}} −\mathrm{2}\lambda^{\mathrm{2}} +\mathrm{3}\lambda−\mathrm{2}=\mathrm{0}\: \\ $$$$\left(\lambda−\mathrm{1}\right)\left(\lambda^{\mathrm{2}} −\lambda+\mathrm{2}\right)\:\:=\:\mathrm{0} \\ $$$$\lambda\:=\:\mathrm{1}\:,\:\frac{\mathrm{1}\pm\:{i}\sqrt{\mathrm{7}}}{\mathrm{2}} \\ $$$${y}_{{h}} \:=\:{A}_{\mathrm{1}} \mathrm{e}^{{x}} +{A}_{\mathrm{2}} \mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}{x}} \left(\mathrm{cos}\:\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\right){x}+\mathrm{sin}\:\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\right)\right) \\ $$$$ \\ $$
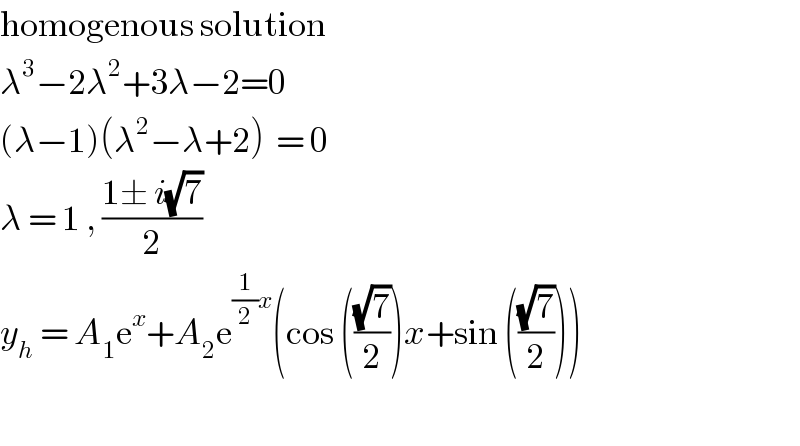
Answered by mathmax by abdo last updated on 29/May/20
![let solve it by laplace transform (e)⇒L(y^((3))) −2L(y^((2)) )+3L(y^′ )−2L(y) =L(sinx) ⇒ x^3 L(y)−x^2 y(0)−xy^′ (0)−y^(′′) (0)−2(x^2 L(y)−xy(0)−y^′ (0)) +3(xL(y)−y(0))−2L(y) =L(sinx) ⇒ (x^3 −2x^2 +3x−2)L(y)−x^2 y(0)−xy^′ (0)−y^((2)) (0)+2xy(0)+2y^′ (0) −3y(0) =L(sinx) ⇒ (x^3 −2x^2 +3x−2)L(y) =L(sinx)+x^2 y(0) +(2−x)y^′ (0) +(2x−3)y(0)+y^((2)) (0) ⇒ L(sinx) =∫_0 ^∞ sint e^(−xt) dt =Im(∫_0 ^∞ e^(it−xt) dt) but ∫_0 ^∞ e^((i−x)t) dt =[(1/(i−x))e^((i−x)t) ]_0 ^∞ =−(1/(i−x)) =(1/(x−i)) =((x+i)/(x^2 +1)) ⇒L(sinx)=(1/(x^2 +1)) ⇒ L(y) =(1/((x^2 +1)(x^3 −2x^2 +3x−2))) +((x^2 +2x−3)/(x^3 −2x^2 +3x−2))y(0)+((2−x)/(x^3 −2x^2 +3x−2))y^′ (0)+((y^((2)) (0))/(x^3 −2x^2 +3x−2)) ⇒y =L^(−1) ((1/((x^2 +1)(x^3 −2x^2 +3x−2))))+y_0 L^(−1) (((x^2 +2x−3)/(x^3 −2x^2 +3x−2)))) +y^′ (0)L^(−1) (((2−x)/(x^3 −2x^2 +3x−2))) +y^((2)) (0)L^(−1) ((1/(x^3 −2x^2 +3x−2))) wehave x^3 −2x^2 +3x−2 =x^3 −x^2 −x^2 +3x−2 =x^2 (x−1)−(x^2 −3x+2) =x^2 (x−1)−(x^2 −x−2x+2) =x^2 (x−1)−{x(x−1)−2(x−1)} =x^2 (x−1)−(x−1)(x−2) =(x−1)(x^2 −x+2) ⇒ F(x) =(1/(x^3 −2x^2 +3x−2)) =(1/((x−1)(x^2 −x+2))) =(a/(x−1)) +((bx+c)/(x^2 −x+2)) ....be continued....](Q95974.png)
$$\mathrm{let}\:\mathrm{solve}\:\mathrm{it}\:\mathrm{by}\:\mathrm{laplace}\:\mathrm{transform}\: \\ $$$$\left(\mathrm{e}\right)\Rightarrow\mathrm{L}\left(\mathrm{y}^{\left.\left(\mathrm{3}\right)\right)} −\mathrm{2L}\left(\mathrm{y}^{\left(\mathrm{2}\right)} \right)+\mathrm{3L}\left(\mathrm{y}^{'} \right)−\mathrm{2L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{sinx}\right)\:\Rightarrow\right. \\ $$$$\mathrm{x}^{\mathrm{3}} \:\mathrm{L}\left(\mathrm{y}\right)−\mathrm{x}^{\mathrm{2}} \mathrm{y}\left(\mathrm{0}\right)−\mathrm{xy}^{'} \left(\mathrm{0}\right)−\mathrm{y}^{''} \left(\mathrm{0}\right)−\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} \mathrm{L}\left(\mathrm{y}\right)−\mathrm{xy}\left(\mathrm{0}\right)−\mathrm{y}^{'} \left(\mathrm{0}\right)\right) \\ $$$$+\mathrm{3}\left(\mathrm{xL}\left(\mathrm{y}\right)−\mathrm{y}\left(\mathrm{0}\right)\right)−\mathrm{2L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{sinx}\right)\:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{2}\right)\mathrm{L}\left(\mathrm{y}\right)−\mathrm{x}^{\mathrm{2}} \mathrm{y}\left(\mathrm{0}\right)−\mathrm{xy}^{'} \left(\mathrm{0}\right)−\mathrm{y}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)+\mathrm{2xy}\left(\mathrm{0}\right)+\mathrm{2y}^{'} \left(\mathrm{0}\right) \\ $$$$−\mathrm{3y}\left(\mathrm{0}\right)\:=\mathrm{L}\left(\mathrm{sinx}\right)\:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{2}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{sinx}\right)+\mathrm{x}^{\mathrm{2}} \mathrm{y}\left(\mathrm{0}\right)\:+\left(\mathrm{2}−\mathrm{x}\right)\mathrm{y}^{'} \left(\mathrm{0}\right)\:+\left(\mathrm{2x}−\mathrm{3}\right)\mathrm{y}\left(\mathrm{0}\right)+\mathrm{y}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{sinx}\right)\:=\int_{\mathrm{0}} ^{\infty} \mathrm{sint}\:\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt}\:=\mathrm{Im}\left(\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{\mathrm{it}−\mathrm{xt}} \mathrm{dt}\right)\:\mathrm{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(\mathrm{i}−\mathrm{x}\right)\mathrm{t}} \mathrm{dt}\:=\left[\frac{\mathrm{1}}{\mathrm{i}−\mathrm{x}}\mathrm{e}^{\left(\mathrm{i}−\mathrm{x}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \:=−\frac{\mathrm{1}}{\mathrm{i}−\mathrm{x}}\:=\frac{\mathrm{1}}{\mathrm{x}−\mathrm{i}}\:=\frac{\mathrm{x}+\mathrm{i}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\mathrm{L}\left(\mathrm{sinx}\right)=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{y}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{2}\right)}\:+\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{3}}{\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{2}}\mathrm{y}\left(\mathrm{0}\right)+\frac{\mathrm{2}−\mathrm{x}}{\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{2}}\mathrm{y}^{'} \left(\mathrm{0}\right)+\frac{\mathrm{y}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)}{\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{2}} \\ $$$$\Rightarrow\mathrm{y}\:=\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{2}\right)}\right)+\mathrm{y}_{\mathrm{0}} \mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}−\mathrm{3}}{\left.\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{2}\right)}\right) \\ $$$$+\mathrm{y}^{'} \left(\mathrm{0}\right)\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{2}−\mathrm{x}}{\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{2}}\right)\:+\mathrm{y}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{2}}\right)\:\mathrm{wehave} \\ $$$$\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{2}\:=\mathrm{x}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} \:−\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{2}\:=\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\mathrm{1}\right)−\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{2}\right) \\ $$$$=\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\mathrm{1}\right)−\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2x}+\mathrm{2}\right)\:=\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\mathrm{1}\right)−\left\{\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)−\mathrm{2}\left(\mathrm{x}−\mathrm{1}\right)\right\} \\ $$$$=\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\mathrm{1}\right)−\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)\:=\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}\right)\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{2}}\:=\frac{\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}\right)}\:=\frac{\mathrm{a}}{\mathrm{x}−\mathrm{1}}\:+\frac{\mathrm{bx}+\mathrm{c}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}} \\ $$$$....\mathrm{be}\:\mathrm{continued}.... \\ $$