Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 95844 by mathmax by abdo last updated on 28/May/20

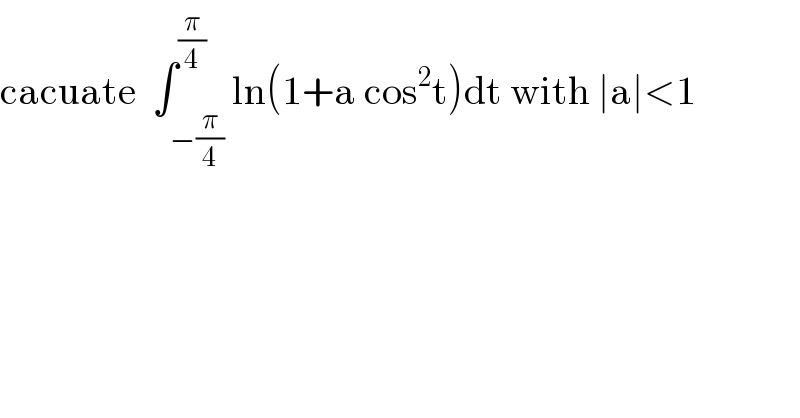
cacuate ∫_(−(π/4)) ^(π/4) ln(1+a cos^2 t)dt with ∣a∣<1

$$\mathrm{cacuate}\:\:\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{a}\:\mathrm{cos}^{\mathrm{2}} \mathrm{t}\right)\mathrm{dt}\:\mathrm{with}\:\mid\mathrm{a}\mid<\mathrm{1} \\ $$

Answered by mathmax by abdo last updated on 29/May/20

let f(a) =∫_(−(π/4)) ^(π/4) ln(1+acos^2 t)dt ⇒f(a) =2∫_0 ^(π/4) ln(1+acos^2 t)dt ⇒ f^′ (a) =2 ∫_0 ^(π/4) ((cos^2 t)/(1+a cos^2 t))dt =(2/a) ∫_0 ^(π/4) ((1+acos^2 t−1)/(1+acos^2 t))dt =(2/a)×(π/4) −(2/a) ∫_0 ^(π/4) (dt/(1+acos^2 t)) =(π/(2a)) −(2/a)∫_0 ^(π/4) (dt/(1+acos^2 t)) we have ∫_0 ^(π/4) (dt/(1+acos^2 t)) =∫_0 ^(π/4) (dt/(1+a((1+cos(2t))/2))) =∫_0 ^(π/4) ((2dt)/(2+a +acos(2t))) =_(2t=u) =∫_0 ^(π/2) (du/(2+a +acosu)) =_(tan((u/2)) =z) ∫_0 ^1 ((2dz)/((1+z^2 )(2+a +a((1−z^2 )/(1+z^2 ))))) =∫_0 ^1 ((2dz)/((2+a)(1+z^2 ) +a−az^2 )) =∫_0 ^1 ((2dz)/(2+a +(2+a−a)z^2 )) =∫_0 ^1 ((2dz)/(2+a+2z^2 )) =(2/(2+a))∫_0 ^1 (dz/(1+(2/(2+a))z^2 )) =_((√(2/(2+a)))z =α) (2/(2+a)) ∫_0 ^(√(2/(2+a))) (((√((2+a)/2))dα)/(1+α^2 )) =(2/(√2))×(1/(√(2+a))) [ arctan(α)]_0 ^(√(2/(2+a))) =((√2)/(√(2+a))) arctan((√(2/(2+a)))) ⇒ f^′ (a) =(π/(2a)) −(2/a)×((√2)/(√(2+a))) arctan((√(2/(2+a)))) ⇒ f(a) =(π/2)ln∣a∣−2∫ (1/a)(√(2/(2+a))) arctan((√(2/(2+a))))da +c changement (√(2/(2+a)))=t give (2/(2+a)) =t^2 ⇒((2+a)/2) =(1/t^2 ) ⇒2+a =(2/t^2 ) ⇒a=(2/t^2 )−2 ⇒ da =2(((−2t)/t^4 )) =((−4)/t^3 ) ⇒ ∫(1/a)(√(2/(2+a)))arctan((√(2/(2+a))))da =∫ (1/((2/t^2 )−2))×t×arctan(t)×(((−4)/t^3 ))dt =−4 ∫ (1/(t^2 ((2/t^2 )−2))) arctan(t)dt =−4 ∫ ((arctan(t))/(2−2t^2 ))dt =2 ∫ ((arctant)/(t^2 −1))dt =∫ ((1/(t−1))−(1/(t+1)))arctan(t)dt =∫ ((arctant)/(t−1))dt−∫ ((arctant)/(t+1))dt (→t =−u) =∫ ((arctant)/(t−1))dt −∫ ((−arctanu)/(−u +1))(−du) =∫ ((arctan(t))/(t−1))dt+∫ ((arctanu)/(u−1))du =2 ∫ ((arctan(t))/(t−1))dt....be continued....

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{acos}^{\mathrm{2}} \mathrm{t}\right)\mathrm{dt}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{acos}^{\mathrm{2}} \mathrm{t}\right)\mathrm{dt}\:\Rightarrow \\ $$ $$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{t}}{\mathrm{1}+\mathrm{a}\:\mathrm{cos}^{\mathrm{2}} \mathrm{t}}\mathrm{dt}\:=\frac{\mathrm{2}}{\mathrm{a}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{1}+\mathrm{acos}^{\mathrm{2}} \mathrm{t}−\mathrm{1}}{\mathrm{1}+\mathrm{acos}^{\mathrm{2}} \mathrm{t}}\mathrm{dt} \\ $$ $$=\frac{\mathrm{2}}{\mathrm{a}}×\frac{\pi}{\mathrm{4}}\:−\frac{\mathrm{2}}{\mathrm{a}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{acos}^{\mathrm{2}} \mathrm{t}}\:=\frac{\pi}{\mathrm{2a}}\:−\frac{\mathrm{2}}{\mathrm{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{acos}^{\mathrm{2}} \mathrm{t}}\:\:\mathrm{we}\:\mathrm{have} \\ $$ $$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{acos}^{\mathrm{2}} \mathrm{t}}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{a}\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2t}\right)}{\mathrm{2}}}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{2dt}}{\mathrm{2}+\mathrm{a}\:+\mathrm{acos}\left(\mathrm{2t}\right)}\:=_{\mathrm{2t}=\mathrm{u}} \\ $$ $$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{du}}{\mathrm{2}+\mathrm{a}\:+\mathrm{acosu}}\:=_{\mathrm{tan}\left(\frac{\mathrm{u}}{\mathrm{2}}\right)\:=\mathrm{z}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2dz}}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{2}+\mathrm{a}\:+\mathrm{a}\frac{\mathrm{1}−\mathrm{z}^{\mathrm{2}} }{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }\right)} \\ $$ $$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2dz}}{\left(\mathrm{2}+\mathrm{a}\right)\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)\:+\mathrm{a}−\mathrm{az}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2dz}}{\mathrm{2}+\mathrm{a}\:+\left(\mathrm{2}+\mathrm{a}−\mathrm{a}\right)\mathrm{z}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2dz}}{\mathrm{2}+\mathrm{a}+\mathrm{2z}^{\mathrm{2}} } \\ $$ $$=\frac{\mathrm{2}}{\mathrm{2}+\mathrm{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{dz}}{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}+\mathrm{a}}\mathrm{z}^{\mathrm{2}} }\:=_{\sqrt{\frac{\mathrm{2}}{\mathrm{2}+\mathrm{a}}}\mathrm{z}\:=\alpha} \:\:\:\frac{\mathrm{2}}{\mathrm{2}+\mathrm{a}}\:\int_{\mathrm{0}} ^{\sqrt{\frac{\mathrm{2}}{\mathrm{2}+\mathrm{a}}}} \:\:\:\:\frac{\sqrt{\frac{\mathrm{2}+\mathrm{a}}{\mathrm{2}}}\mathrm{d}\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} } \\ $$ $$=\frac{\mathrm{2}}{\sqrt{\mathrm{2}}}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}+\mathrm{a}}}\:\left[\:\mathrm{arctan}\left(\alpha\right)\right]_{\mathrm{0}} ^{\sqrt{\frac{\mathrm{2}}{\mathrm{2}+\mathrm{a}}}} =\frac{\sqrt{\mathrm{2}}}{\sqrt{\mathrm{2}+\mathrm{a}}}\:\mathrm{arctan}\left(\sqrt{\frac{\mathrm{2}}{\mathrm{2}+\mathrm{a}}}\right)\:\Rightarrow \\ $$ $$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\frac{\pi}{\mathrm{2a}}\:−\frac{\mathrm{2}}{\mathrm{a}}×\frac{\sqrt{\mathrm{2}}}{\sqrt{\mathrm{2}+\mathrm{a}}}\:\mathrm{arctan}\left(\sqrt{\frac{\mathrm{2}}{\mathrm{2}+\mathrm{a}}}\right)\:\Rightarrow \\ $$ $$\mathrm{f}\left(\mathrm{a}\right)\:=\frac{\pi}{\mathrm{2}}\mathrm{ln}\mid\mathrm{a}\mid−\mathrm{2}\int\:\:\frac{\mathrm{1}}{\mathrm{a}}\sqrt{\frac{\mathrm{2}}{\mathrm{2}+\mathrm{a}}}\:\mathrm{arctan}\left(\sqrt{\frac{\mathrm{2}}{\mathrm{2}+\mathrm{a}}}\right)\mathrm{da}\:+\mathrm{c} \\ $$ $$\mathrm{changement}\:\sqrt{\frac{\mathrm{2}}{\mathrm{2}+\mathrm{a}}}=\mathrm{t}\:\mathrm{give}\:\:\frac{\mathrm{2}}{\mathrm{2}+\mathrm{a}}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\frac{\mathrm{2}+\mathrm{a}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\:\Rightarrow\mathrm{2}+\mathrm{a}\:=\frac{\mathrm{2}}{\mathrm{t}^{\mathrm{2}} }\:\Rightarrow\mathrm{a}=\frac{\mathrm{2}}{\mathrm{t}^{\mathrm{2}} }−\mathrm{2}\:\Rightarrow \\ $$ $$\mathrm{da}\:=\mathrm{2}\left(\frac{−\mathrm{2t}}{\mathrm{t}^{\mathrm{4}} }\right)\:=\frac{−\mathrm{4}}{\mathrm{t}^{\mathrm{3}} }\:\Rightarrow \\ $$ $$\int\frac{\mathrm{1}}{\mathrm{a}}\sqrt{\frac{\mathrm{2}}{\mathrm{2}+\mathrm{a}}}\mathrm{arctan}\left(\sqrt{\frac{\mathrm{2}}{\mathrm{2}+\mathrm{a}}}\right)\mathrm{da}\:=\int\:\frac{\mathrm{1}}{\frac{\mathrm{2}}{\mathrm{t}^{\mathrm{2}} }−\mathrm{2}}×\mathrm{t}×\mathrm{arctan}\left(\mathrm{t}\right)×\left(\frac{−\mathrm{4}}{\mathrm{t}^{\mathrm{3}} }\right)\mathrm{dt} \\ $$ $$=−\mathrm{4}\:\int\:\:\:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \left(\frac{\mathrm{2}}{\mathrm{t}^{\mathrm{2}} }−\mathrm{2}\right)}\:\mathrm{arctan}\left(\mathrm{t}\right)\mathrm{dt}\:=−\mathrm{4}\:\int\:\:\frac{\mathrm{arctan}\left(\mathrm{t}\right)}{\mathrm{2}−\mathrm{2t}^{\mathrm{2}} }\mathrm{dt} \\ $$ $$=\mathrm{2}\:\int\:\frac{\mathrm{arctant}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt}\:\:=\int\:\:\left(\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}\right)\mathrm{arctan}\left(\mathrm{t}\right)\mathrm{dt} \\ $$ $$=\int\:\:\frac{\mathrm{arctant}}{\mathrm{t}−\mathrm{1}}\mathrm{dt}−\int\:\frac{\mathrm{arctant}}{\mathrm{t}+\mathrm{1}}\mathrm{dt}\:\left(\rightarrow\mathrm{t}\:=−\mathrm{u}\right) \\ $$ $$=\int\:\frac{\mathrm{arctant}}{\mathrm{t}−\mathrm{1}}\mathrm{dt}\:−\int\:\:\frac{−\mathrm{arctanu}}{−\mathrm{u}\:+\mathrm{1}}\left(−\mathrm{du}\right)\:=\int\:\frac{\mathrm{arctan}\left(\mathrm{t}\right)}{\mathrm{t}−\mathrm{1}}\mathrm{dt}+\int\:\:\frac{\mathrm{arctanu}}{\mathrm{u}−\mathrm{1}}\mathrm{du} \\ $$ $$=\mathrm{2}\:\int\:\frac{\mathrm{arctan}\left(\mathrm{t}\right)}{\mathrm{t}−\mathrm{1}}\mathrm{dt}....\mathrm{be}\:\mathrm{continued}.... \\ $$ $$ \\ $$

Commented bymaths mind last updated on 21/Jun/20

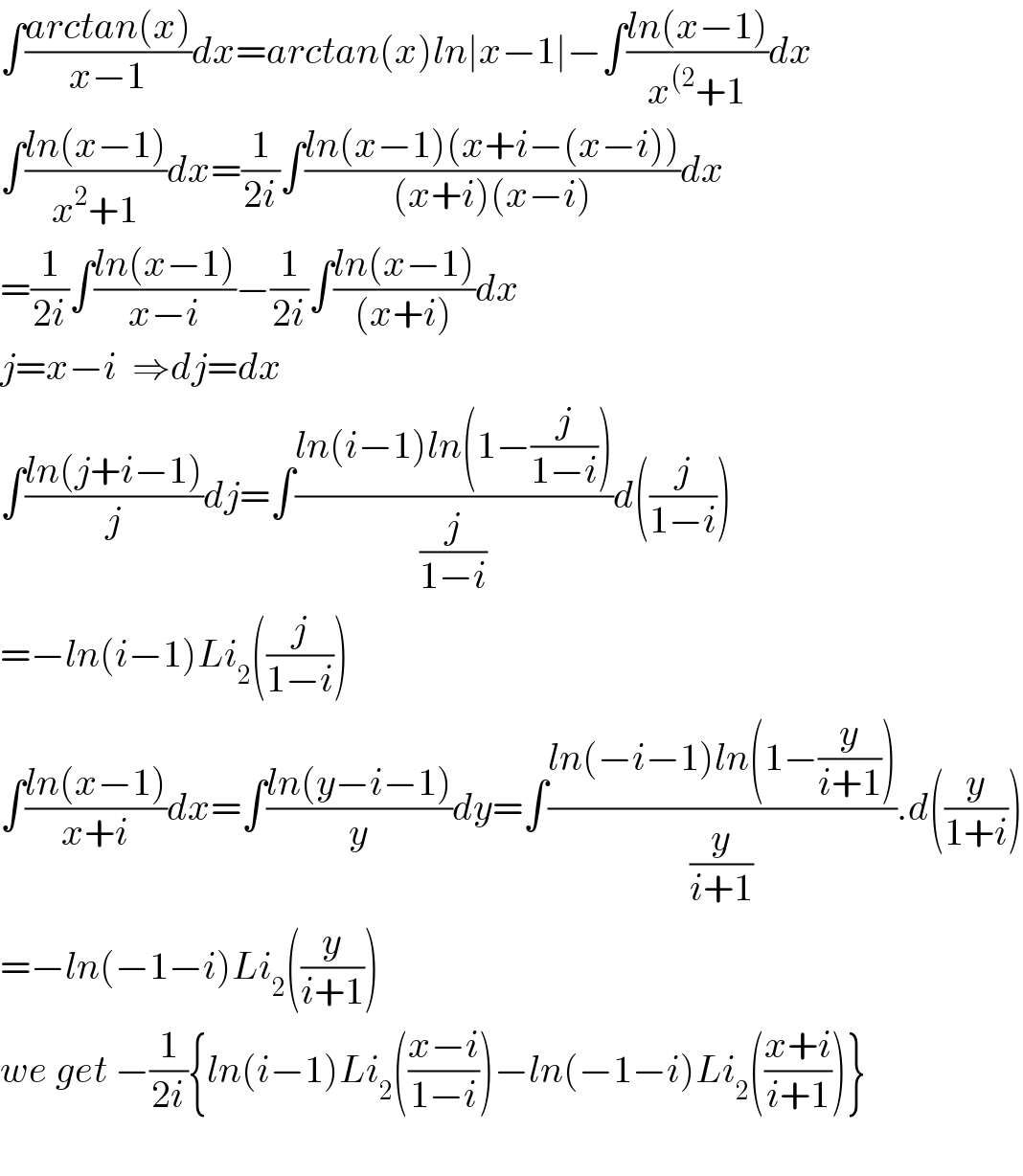
∫((arctan(x))/(x−1))dx=arctan(x)ln∣x−1∣−∫((ln(x−1))/(x^((2) +1))dx ∫((ln(x−1))/(x^2 +1))dx=(1/(2i))∫((ln(x−1)(x+i−(x−i)))/((x+i)(x−i)))dx =(1/(2i))∫((ln(x−1))/(x−i))−(1/(2i))∫((ln(x−1))/((x+i)))dx j=x−i ⇒dj=dx ∫((ln(j+i−1))/j)dj=∫((ln(i−1)ln(1−(j/(1−i))))/(j/(1−i)))d((j/(1−i))) =−ln(i−1)Li_2 ((j/(1−i))) ∫((ln(x−1))/(x+i))dx=∫((ln(y−i−1))/y)dy=∫((ln(−i−1)ln(1−(y/(i+1))))/(y/(i+1))).d((y/(1+i))) =−ln(−1−i)Li_2 ((y/(i+1))) we get −(1/(2i)){ln(i−1)Li_2 (((x−i)/(1−i)))−ln(−1−i)Li_2 (((x+i)/(i+1)))}

$$\int\frac{{arctan}\left({x}\right)}{{x}−\mathrm{1}}{dx}={arctan}\left({x}\right){ln}\mid{x}−\mathrm{1}\mid−\int\frac{{ln}\left({x}−\mathrm{1}\right)}{{x}^{\left(\mathrm{2}\right.} +\mathrm{1}}{dx} \\ $$ $$\int\frac{{ln}\left({x}−\mathrm{1}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{2}{i}}\int\frac{{ln}\left({x}−\mathrm{1}\right)\left({x}+{i}−\left({x}−{i}\right)\right)}{\left({x}+{i}\right)\left({x}−{i}\right)}{dx} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}{i}}\int\frac{{ln}\left({x}−\mathrm{1}\right)}{{x}−{i}}−\frac{\mathrm{1}}{\mathrm{2}{i}}\int\frac{{ln}\left({x}−\mathrm{1}\right)}{\left({x}+{i}\right)}{dx} \\ $$ $${j}={x}−{i}\:\:\Rightarrow{dj}={dx} \\ $$ $$\int\frac{{ln}\left({j}+{i}−\mathrm{1}\right)}{{j}}{dj}=\int\frac{{ln}\left({i}−\mathrm{1}\right){ln}\left(\mathrm{1}−\frac{{j}}{\mathrm{1}−{i}}\right)}{\frac{{j}}{\mathrm{1}−{i}}}{d}\left(\frac{{j}}{\mathrm{1}−{i}}\right) \\ $$ $$=−{ln}\left({i}−\mathrm{1}\right){Li}_{\mathrm{2}} \left(\frac{{j}}{\mathrm{1}−{i}}\right) \\ $$ $$\int\frac{{ln}\left({x}−\mathrm{1}\right)}{{x}+{i}}{dx}=\int\frac{{ln}\left({y}−{i}−\mathrm{1}\right)}{{y}}{dy}=\int\frac{{ln}\left(−{i}−\mathrm{1}\right){ln}\left(\mathrm{1}−\frac{{y}}{{i}+\mathrm{1}}\right)}{\frac{{y}}{{i}+\mathrm{1}}}.{d}\left(\frac{{y}}{\mathrm{1}+{i}}\right) \\ $$ $$=−{ln}\left(−\mathrm{1}−{i}\right){Li}_{\mathrm{2}} \left(\frac{{y}}{{i}+\mathrm{1}}\right) \\ $$ $${we}\:{get}\:−\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{{ln}\left({i}−\mathrm{1}\right){Li}_{\mathrm{2}} \left(\frac{{x}−{i}}{\mathrm{1}−{i}}\right)−{ln}\left(−\mathrm{1}−{i}\right){Li}_{\mathrm{2}} \left(\frac{{x}+{i}}{{i}+\mathrm{1}}\right)\right\} \\ $$ $$ \\ $$

Answered by mathmax by abdo last updated on 29/May/20

let determine f(a) =∫_(−(π/4)) ^(π/4) ln(1+acos^2 x)dx at form of serie f(a) =2∫_0 ^(π/4) ln(1+a ×((1+cos(2x))/2))dx =2 ∫_0 ^(π/4) ln(2+a +acos(2x))dx −2×(π/4)ln(2) +2 ∫_0 ^(π/4) ln{ (2+a)(1+(a/(2+a))cos(2x)}dx =−(π/2)ln(2)+(π/2)ln(2+a) +2 ∫_0 ^(π/4) ln(1+(a/(2+a))cos(2x))dx we have ln^′ (1+u) =(1/(1+u)) =Σ_(n=0) ^∞ (−1)^n u^n ⇒ln(1+u) =Σ_(n=0) ^∞ (((−1)^n u^(n+1) )/(n+1)) +c(c=0) =Σ_(n=1) ^∞ (((−1)^(n−1) u^n )/n) ⇒∫_0 ^(π/4) ln(1+(a/(a+2)) cos(2x))dx =_(2x=t) ∫_0 ^(π/2) ln(1+(a/(a+2))cost)(dt/2) =(1/2) ∫_0 ^(π/2) (Σ_(n=1) ^∞ (((−1)^(n−1) )/n)((a/(a+2)) cost)^n )dt =(1/2)Σ_(n=1) ^∞ (((−1)^(n−1) )/n)((a/(a+2)))^n ∫_0 ^(π/2) cos^n t dt =(1/2)Σ_(n=1) ^∞ (((−1)^(n−1) )/n)w_n ((a/(a+2)))^n with w_n =∫_0 ^(π/2) cos^n t dt (wsllis integral) ⇒ f(a) =(π/2)(ln(2+a)−ln2) +Σ_(n=1) ^∞ (((−1)^(n−1) )/n)w_n ((a/(a+2)))^n ....be continued...

$$\mathrm{let}\:\mathrm{determine}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{acos}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dx}\:\mathrm{at}\:\mathrm{form}\:\mathrm{of}\:\mathrm{serie} \\ $$ $$\mathrm{f}\left(\mathrm{a}\right)\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{a}\:×\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}\right)\mathrm{dx}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{2}+\mathrm{a}\:+\mathrm{acos}\left(\mathrm{2x}\right)\right)\mathrm{dx} \\ $$ $$−\mathrm{2}×\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left\{\:\left(\mathrm{2}+\mathrm{a}\right)\left(\mathrm{1}+\frac{\mathrm{a}}{\mathrm{2}+\mathrm{a}}\mathrm{cos}\left(\mathrm{2x}\right)\right\}\mathrm{dx}\right. \\ $$ $$=−\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)+\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}+\mathrm{a}\right)\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{a}}{\mathrm{2}+\mathrm{a}}\mathrm{cos}\left(\mathrm{2x}\right)\right)\mathrm{dx} \\ $$ $$\mathrm{we}\:\mathrm{have}\:\mathrm{ln}^{'} \left(\mathrm{1}+\mathrm{u}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{n}} \:\Rightarrow\mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\:+\mathrm{c}\left(\mathrm{c}=\mathrm{0}\right) \\ $$ $$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\mathrm{u}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{a}}{\mathrm{a}+\mathrm{2}}\:\mathrm{cos}\left(\mathrm{2x}\right)\right)\mathrm{dx} \\ $$ $$=_{\mathrm{2x}=\mathrm{t}} \:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{a}}{\mathrm{a}+\mathrm{2}}\mathrm{cost}\right)\frac{\mathrm{dt}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\left(\frac{\mathrm{a}}{\mathrm{a}+\mathrm{2}}\:\mathrm{cost}\right)^{\mathrm{n}} \right)\mathrm{dt} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\left(\frac{\mathrm{a}}{\mathrm{a}+\mathrm{2}}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{n}} \mathrm{t}\:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\mathrm{w}_{\mathrm{n}} \left(\frac{\mathrm{a}}{\mathrm{a}+\mathrm{2}}\right)^{\mathrm{n}} \\ $$ $$\mathrm{with}\:\mathrm{w}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{n}} \:\mathrm{t}\:\mathrm{dt}\:\left(\mathrm{wsllis}\:\mathrm{integral}\right)\:\Rightarrow \\ $$ $$\mathrm{f}\left(\mathrm{a}\right)\:=\frac{\pi}{\mathrm{2}}\left(\mathrm{ln}\left(\mathrm{2}+\mathrm{a}\right)−\mathrm{ln2}\right)\:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\mathrm{w}_{\mathrm{n}} \left(\frac{\mathrm{a}}{\mathrm{a}+\mathrm{2}}\right)^{\mathrm{n}} \\ $$ $$....\mathrm{be}\:\mathrm{continued}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com