find a common roots from the two quadratic eq 24x^2 +(p+4)x−1=0 and 6x^2 +11x+p+2=0


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 96189 by bemath last updated on 30/May/20

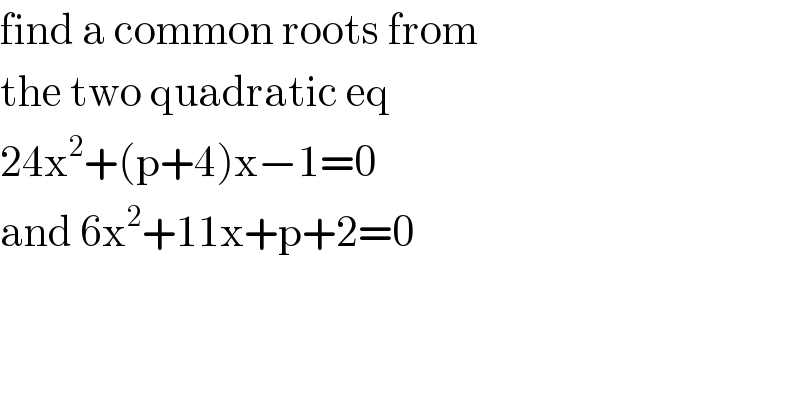
$find a common roots from$ $the two quadratic eq$ ${24 x}^{2} + (p + 4) x - 1 = 0$ $and {6 x}^{2} + 11 x + p + 2 = 0$
	Answered by john santu last updated on 30/May/20

	$by {Wildberger}^{'} s theorem$ $if two quadratic eq : x^{2} + Ax + B = 0$ $and x^{2} + Cx + D = 0 have a common$ $roots {it}^{'} s \Rightarrow x = \frac{D - B}{A - C}$ $(i) x^{2} + (\frac{p + 4}{24}) x - \frac{1}{24} = 0$ $(ii) x^{2} + (\frac{11}{6}) x + (\frac{p + 2}{6}) = 0$ $s o t h e c o m m o n r o o t s$ $i s x = \frac{\frac{p + 2}{6} + \frac{1}{24}}{(\frac{p + 4}{24}) - \frac{11}{6}} = \frac{4 p + 9}{p + 4 - 44}$ $x = \frac{4 p + 9}{p - 40}$
	Commented by bemath last updated on 30/May/20
	wow ... I just found out the theorem mister
	Commented by mr W last updated on 30/May/20

	$o n l y f o r c e r t a i n v a l u e s o f p h a v e b o t h$ $e q u a t i o n s a c o m m o n r o o t .$
	Commented by john santu last updated on 30/May/20
	Yes, right
	Answered by mr W last updated on 30/May/20

	${l e t}^{'} s s a y e q n . 1 h a s r o o t s : α, β$ $e q n . 2 h a s r o o t s : β, γ$ $α + β = - \frac{p + 4}{24}$ $α β = - \frac{1}{24}$ $β + γ = - \frac{11}{6}$ $β γ = \frac{p + 2}{6}$ $\Rightarrow (\frac{p + 4}{24} + β) β = \frac{1}{24} . . . (i)$ $\Rightarrow (\frac{11}{6} + β) β = - \frac{p + 2}{6} . . . (i i)$ $f r o m (i i) :$ $\frac{p + 4}{24} = \frac{1}{12} - \frac{1}{4} (\frac{11}{6} + β) β$ $p u t t h i s i n t o (i) :$ $6 β^{3} - 13 β^{2} - 2 β + 1 = 0$ $\Rightarrow (3 β + 1) (2 β^{2} - 5 β + 1) = 0$ $\Rightarrow 3 β + 1 = 0 \Rightarrow β = - \frac{1}{3}$ $\Rightarrow 2 β^{2} - 5 β + 1 = 0 \Rightarrow β = \frac{5 \pm \sqrt{17}}{4}$ $i . e . t h e c o m m o n r o o t c a n b e$ $- \frac{1}{3}, \frac{5 - \sqrt{17}}{4}, \frac{5 + \sqrt{17}}{4}$ $p = - 2 - 6 (\frac{11}{6} + β) β$ $\Rightarrow p = 1$ $\Rightarrow p = - \frac{63 - 13 \sqrt{17}}{2} \approx - 4.7$ $\Rightarrow p = - \frac{63 + 13 \sqrt{17}}{2} \approx - 58.3$
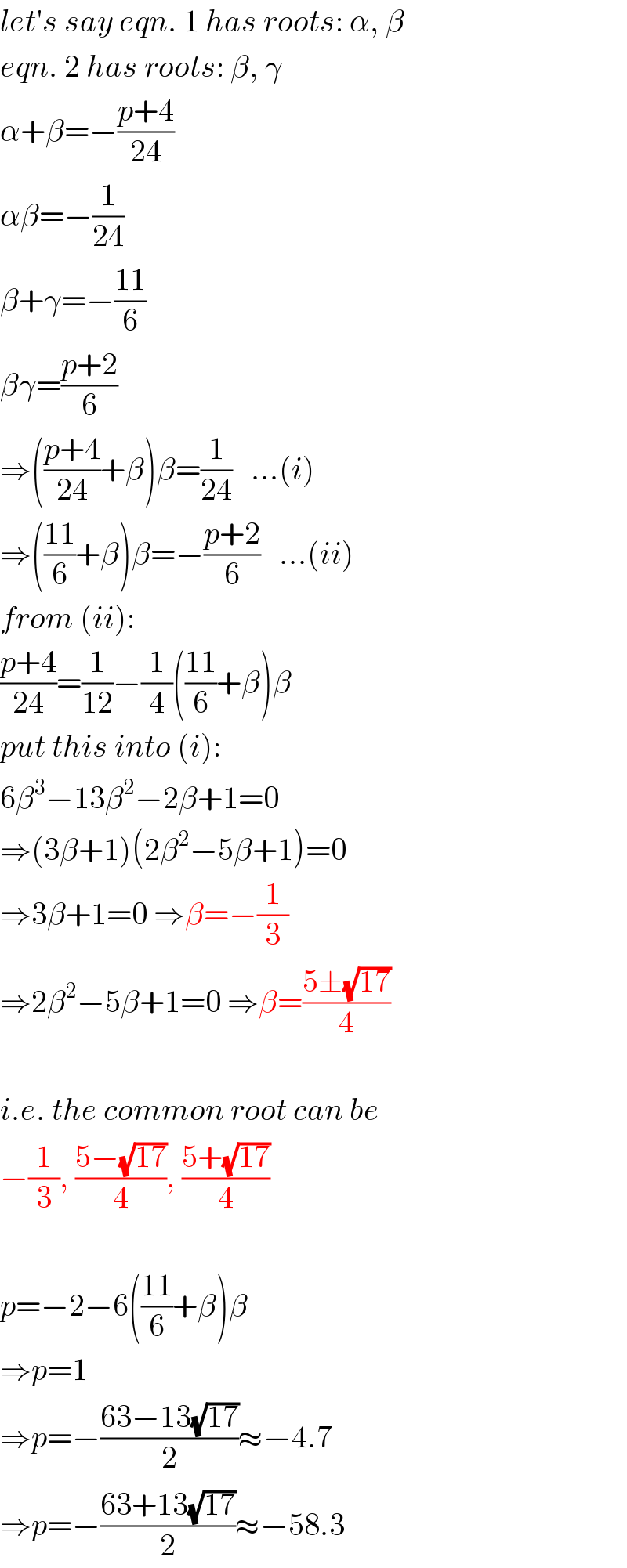
	Answered by 1549442205 last updated on 30/May/20
	$Denoting x_0 common root of two equations.Then { (( 24x_0 ^2 +(p+4)x_0 −1=0(1))),((6x_0 ^2 +11x_0 +p+2=0 (2))) :} ⇔ { ((24x_0 ^2 +(p+4)x_0 −1=0)),((24x_0 +44x_0 +4p+8=0)) :} ⇒(p+4)x_0 −1=44x_0 +4p+8 ⇒(p−40)x_0 =4p+9⇒x_0 =((4p+9)/(p−40)).Replace into (2) ⇒6(((4p+9)/(p−40)))^2 +11(((4p+9)/(p−40)))+p+2=0 ⇔6(16p^2 +72p+81)+11(4p^2 −151p−360) +(p+2)(p^2 −80p+1600)=0⇔ 140p^2 −1229p−3474+p^3 −78p^2 +1440p +3200=0⇔p^3 +62p^2 +211p−274=0 ⇔(p−1)(p^2 +63p+274)=0 a/p=1⇒x_0 =((−1)/3) b/p^2 +63p+274=0⇔p=((−63±13(√(17)))/2) ⇒x_0 ∈{((5−(√(17)))/4);(((√(17))+5)/4)} Thus,two given equations have three common$
	$Denoting x_{0} common root of two equations . Then$ ${\begin{cases} {24 x}_{0}^{2} + (p + 4) x_{0} - 1 = 0 (1) \\ {6 x}_{0}^{2} + {11 x}_{0} + p + 2 = 0 (2) \end{cases}$ $\Leftrightarrow {\begin{cases} {24 x}_{0}^{2} + (p + 4) x_{0} - 1 = 0 \\ {24 x}_{0} + {44 x}_{0} + 4 p + 8 = 0 \end{cases}$ $\Rightarrow (p + 4) x_{0} - 1 = {44 x}_{0} + 4 p + 8$ $\Rightarrow (p - 40) x_{0} = 4 p + 9 \Rightarrow x_{0} = \frac{4 p + 9}{p - 40} . Replace into (2)$ $\Rightarrow 6 {(\frac{4 p + 9}{p - 40})}^{2} + 11 (\frac{4 p + 9}{p - 40}) + p + 2 = 0$ $\Leftrightarrow 6 ({16 p}^{2} + 72 p + 81) + 11 ({4 p}^{2} - 151 p - 360)$ $+ (p + 2) (p^{2} - 80 p + 1600) = 0 \Leftrightarrow$ ${140 p}^{2} - 1229 p - 3474 + p^{3} - {78 p}^{2} + 1440 p$ $+ 3200 = 0 \Leftrightarrow p^{3} + {62 p}^{2} + 211 p - 274 = 0$ $\Leftrightarrow (p - 1) (p^{2} + 63 p + 274) = 0$ $a / p = 1 \Rightarrow x_{0} = \frac{- 1}{3}$ $b / p^{2} + 63 p + 274 = 0 \Leftrightarrow p = \frac{- 63 \pm 13 \sqrt{17}}{2}$ $\Rightarrow x_{0} \in {\frac{5 - \sqrt{17}}{4}; \frac{\sqrt{17} + 5}{4}}$ $Thus, two given equations have three$ $common$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum