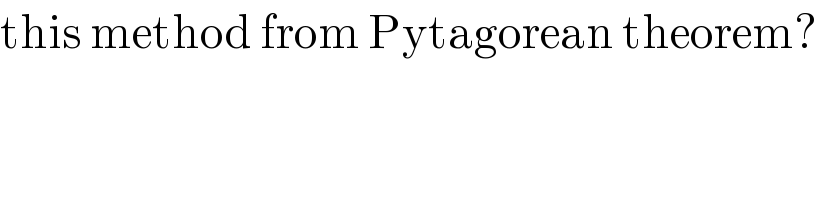Find the shortest distance from the point P(2,−3,5) to the line L ((x+3)/2)=((y−1)/(−3))=((z−2)/4)


Question and Answers Forum

All Questions Topic List
Vector Questions
Previous in All Question Next in All Question
Previous in Vector Next in Vector
Question Number 96240 by mr W last updated on 30/May/20

$F i n d t h e s h o r t e s t d i s t a n c e f r o m t h e$ $p o i n t P (2, - 3, 5) t o t h e l i n e L$ $\frac{x + 3}{2} = \frac{y - 1}{- 3} = \frac{z - 2}{4}$
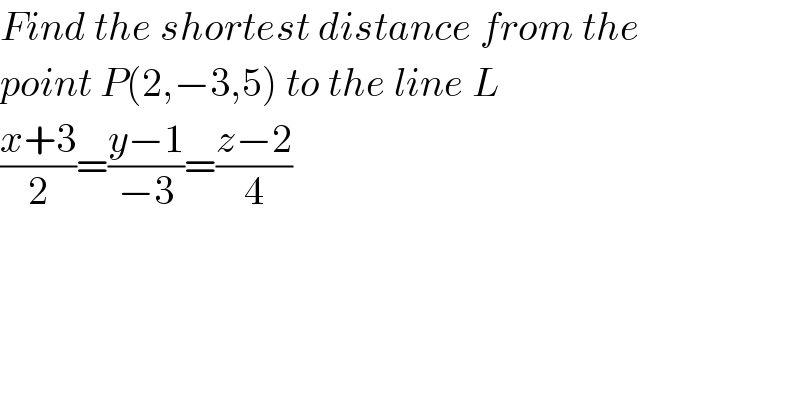
	Answered by 1549442205 last updated on 31/May/20

	$Denote Q be the point on L such that$ $PQ ⊥ L \Rightarrow Q (2 t - 3; - 3 t + 1; 4 t + 2) . Then$ $\vec{PQ} = (2 t - 5; - 3 t + 4; 4 t - 3) . The direction$ $vector of L is \vec{p} = (2; - 3; 4) perpemdicular$ $to \vec{PQ} . Hence, \vec{p} . \vec{PQ} = 0 \Leftrightarrow 2 (2 t - 5) + 3 (3 t - 4)$ $+ 4 (4 t - 3) \Leftrightarrow 29 t - 34 = 0 \Rightarrow t = \frac{34}{29} . From that$ $\vec{PQ} = (\frac{- 77}{29}; \frac{14}{29}; \frac{49}{29}) \Rightarrow PQ = \frac{7 \sqrt{1 \overset{2}{1} + 2^{2} + 7^{2}}}{29} =$ $\frac{7 \sqrt{174}}{29} is shortest distance from P to L$
	Commented by mr W last updated on 31/May/20

	$t h a n k y o u s i r!$
	Answered by john santu last updated on 31/May/20

	$let S (2 s - 3, - 3 s + 1, 5 s + 2) a point$ $on line L . take vector PS = (2 s - 5, - 3 s + 4, 5 s - 3)$ $PS ⊥ n = (2, - 3, 4)$ $4 s - 10 + 9 s - 12 + 20 s - 12 = 0$ $33 s = 34 \Rightarrow s = \frac{34}{33}$ $PS (- \frac{97}{33}, \frac{30}{33}, \frac{71}{33}) .$ $∣ PS ∣ = \frac{\sqrt{15, 350}}{33} \approx 3.754397483$
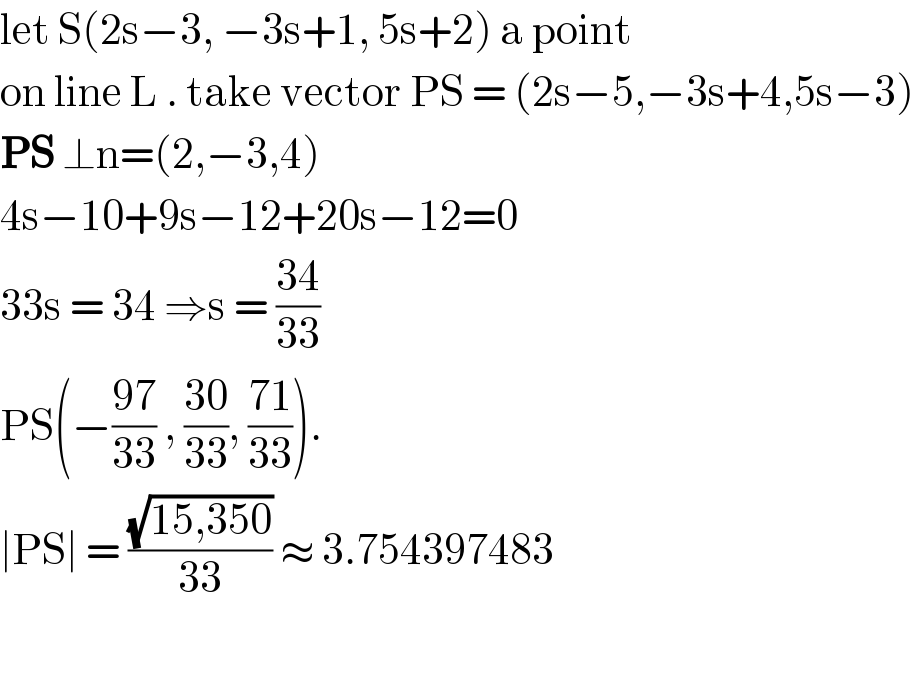
	Commented by mr W last updated on 31/May/20

	$t h a n k y o u s i r!$ $t y p o i n f i r s t l i n e 5 s + 2 ?$ $s = \frac{34}{29} ?$
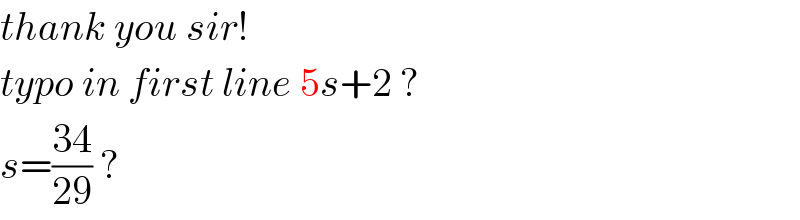
	Commented by bobhans last updated on 31/May/20

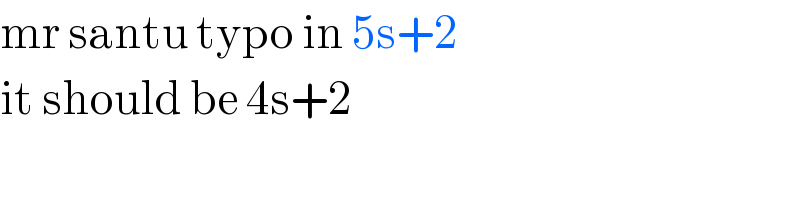
	$mr santu typo in 5 s + 2$ $it should be 4 s + 2$
	Answered by mr W last updated on 31/May/20

	$M E T H O D I$ $a n y p o i n t o n l i n e Q :$ $x = - 3 + 2 k$ $y = 1 - 3 k$ $z = 2 + 4 k$ $d i s t a n c e P Q = d$ $D = d^{2} = {(2 + 3 - 2 k)}^{2} + {(- 3 - 1 + 3 k)}^{2} + {(5 - 2 - 4 k)}^{2}$ $D = {(2 k - 5)}^{2} + {(3 k - 4)}^{2} + {(4 k - 3)}^{2}$ $s u c h t h a t d i s m i n i m u m :$ $\frac{d D}{d k} = 2 (2 k - 5) 2 + 2 (3 k - 4) 3 + 2 (4 k - 3) 4 = 0$ $\Rightarrow 29 k = 34$ $\Rightarrow k = \frac{34}{29}$ $d_{m i n} = \sqrt{{(2 \times \frac{34}{29} - 5)}^{2} + {(3 \times \frac{34}{29} - 4)}^{2} + {(4 \times \frac{34}{29} - 3)}^{2}} = \frac{7 \sqrt{174}}{29}$ $M E T H O D I I$ $k n o w n p o i n t o n l i n e R (- 3, 1, 2)$ $\vec{P R} = (5, - 4, 3)$ $\vec{l} = (2, - 3, 4)$ $\cos θ = \frac{P R \cdot l}{∣ P R ∣∣ l ∣}$ $d =∣ P R ∣ \sin θ =∣ P R ∣ \sqrt{1 - {(\frac{P R \cdot l}{∣ P R ∣∣ l ∣})}^{2}}$ $d = \sqrt{∣ P R ∣^{2} - \frac{{(P R \cdot l)}^{2}}{∣ l ∣^{2}}}$ $d = \sqrt{5^{2} + 4^{2} + 3^{2} - \frac{{(5 \times 2 + 4 \times 3 + 3 \times 4)}^{2}}{2^{2} + 3^{2} + 4^{2}}}$ $d = \sqrt{50 - \frac{34^{2}}{29}} = \frac{7 \sqrt{174}}{29}$ $M E T H O D I I I$ $p l a n e p e r p e n d i c u l a r t o l i n e L i s$ $2 x - 3 y + 4 z + s = 0$ $p o i n t P i s o n t h e p l a n e :$ $2 \times 2 - 3 \times (- 3) + 4 \times 5 + s = 0$ $s = - 33$ $\Rightarrow 2 x - 3 y + 4 z - 33 = 0$ $i n t e r s e c t i o n o f l i n e w i t h p l a n e a t Q :$ $x = - 3 + 2 k$ $y = 1 - 3 k$ $z = 2 + 4 k$ $2 (- 3 + 2 k) - 3 (1 - 3 k) + 4 (2 + 4 k) - 33 = 0$ $29 k - 34 = 0$ $\Rightarrow k = \frac{34}{29}$ $P Q = \sqrt{{(2 + 3 - 2 k)}^{2} + {(- 3 - 1 + 3 k)}^{2} + {(5 - 2 - 4 k)}^{2}}$ $P Q = \sqrt{{(5 - 2 k)}^{2} + {(- 4 + 3 k)}^{2} + {(3 - 4 k)}^{2}}$ $P Q = \sqrt{{(5 - 2 \times \frac{34}{29})}^{2} + {(- 4 + 3 \times \frac{34}{29})}^{2} + {(3 - 4 \times \frac{34}{29})}^{2}}$ $d_{m i n} = P Q = \frac{7 \sqrt{174}}{29}$ $M E T H O D I V$ $p o i n t o n l i n e Q (- 3 + 2 k, 1 - 3 k, 2 + 4 k)$ $\vec{l} = (2, - 3, 4)$ $\vec{P Q} = (2 + 3 - 2 k, - 3 - 1 + 3 k, 5 - 2 - 4 k)$ $\vec{P Q} = (5 - 2 k, - 4 + 3 k, 3 - 4 k)$ $s u c h t h a t \vec{P Q} ⊥ \vec{l} :$ $(5 - 2 k) \times 2 \times (- 4 + 3 k) \times (- 3) + (3 - 4 k) \times 4 = 0$ $\Rightarrow k = \frac{34}{29}$ $d_{m i n} =∣ P Q ∣= \sqrt{{(5 - 2 \times \frac{34}{29})}^{2} + {(- 4 + 3 \times \frac{34}{29})}^{2} + {(3 - 4 \times \frac{34}{29})}^{2}}$ $= \frac{7 \sqrt{174}}{29}$ $M E T H O D V$ $k n o w n p o i n t o n l i n e R (- 3, 1, 2)$ $\vec{P R} = (5, - 4, 3)$ $\vec{l} = (2, - 3, 4)$ $∣ \vec{l} ∣= \sqrt{2^{2} + 3^{2} + 4^{2}} = \sqrt{29}$ $\vec{P R} \times \vec{l} = (5, - 4, 3) \times (2, - 3, 4) = (- 7, - 14, - 7)$ $∣ \vec{P R} \times \vec{l} ∣= \sqrt{7^{2} + 14^{2} + 7^{2}} = 7 \sqrt{6}$ $d = \frac{∣ P R \times \vec{l} ∣}{∣ \vec{l} ∣} = \frac{7 \sqrt{6}}{\sqrt{29}} = \frac{7 \sqrt{174}}{29}$
	Commented by bobhans last updated on 31/May/20

	$waw ==== great$
	Commented by mr W last updated on 31/May/20

	$M e t h o d I I i s m y f a v o u r i t e m e t h o d$ $d_{m i n} = \sqrt{∣ \vec{R P} ∣^{2} - \frac{{(\vec{R P} ∙ \vec{l})}^{2}}{∣ \vec{l} ∣^{2}}}$ $t h i s f o r m u l a i s n o t t e a c h e d i n s c h o o l$ $a n d i n b o o k .$
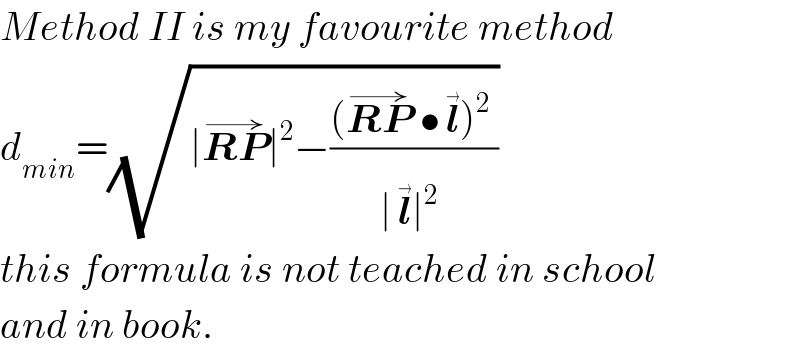
	Commented by mr W last updated on 31/May/20

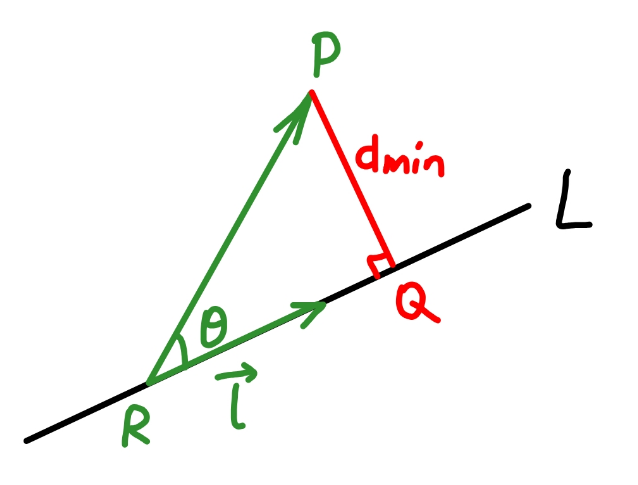
	Commented by bobhans last updated on 31/May/20
	whether the point R is arbitrarily provided it lies on the L line
	Commented by bobhans last updated on 31/May/20

	$this method from Pytagorean theorem ?$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum