Question and Answers Forum
Question Number 96241 by joki last updated on 30/May/20

Answered by 1549442205 last updated on 31/May/20
![It is easy to see that x∈{0,1} don′t satisfy and x∈{2,4} satisfying the given equation We prove that 2^x >x^2 for any x ≥5 Indeed,consider the function f(x)= 2^x −x^2 .We have f ′ (x)=2^x ln2−2x, f ′′(x)=2^x ln^2 2−2>32ln^2 2−2>0 Hence,f ′(x) is increasing function on ]5;+∞)⇒f ′(x)>f ′(5)=32ln2−10>0 This show that the function f(x)=2^x −x^2 is increasing on [5;+∞)⇒f(x)>f(5)=2^5 −25>0 ⇒2^x −x^2 >0⇒2^x >x^2 for every x≥5. Thus,the numbers x satisfy the given equation are x∈{2;4}](Q96248.png)
Answered by mr W last updated on 31/May/20
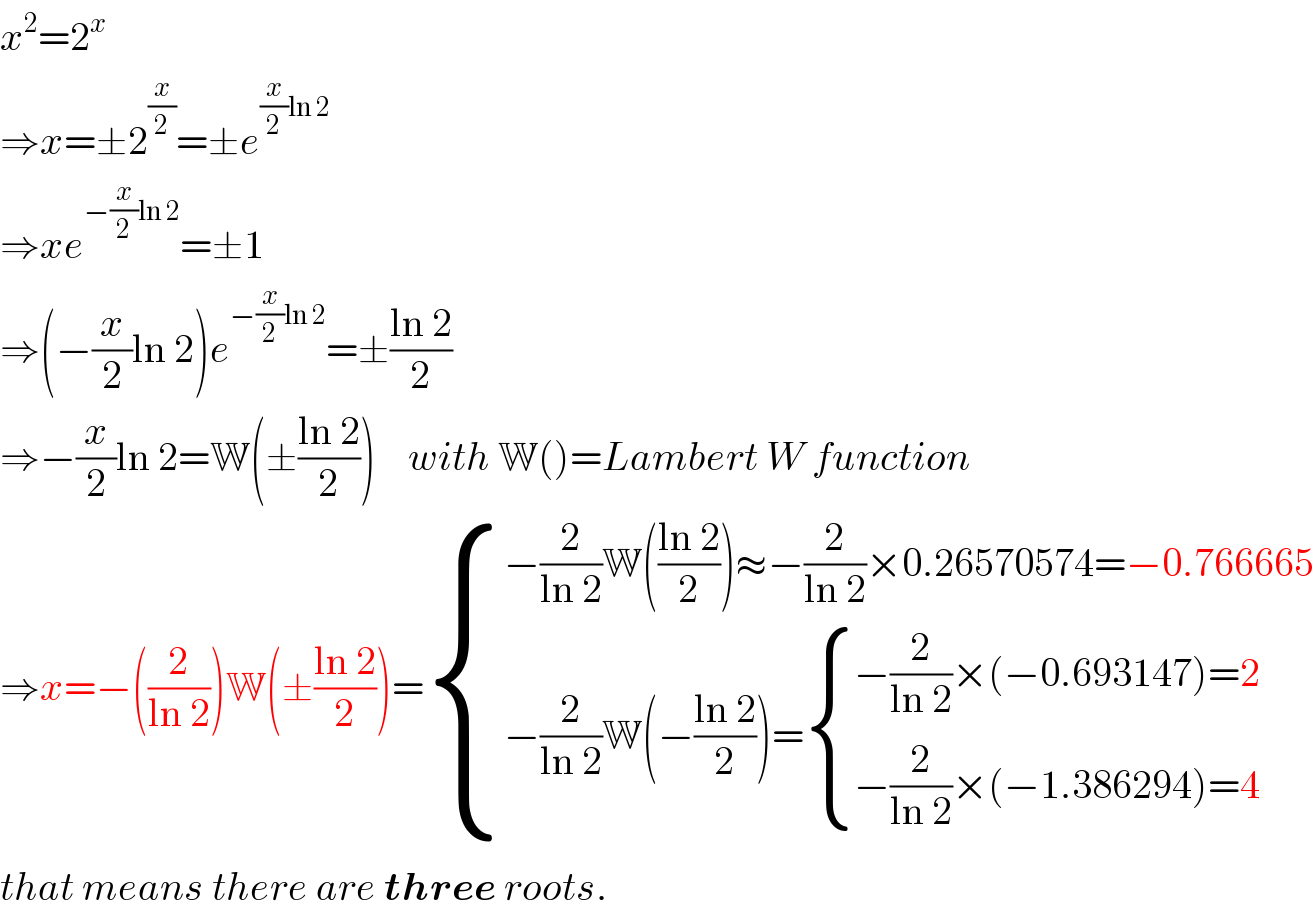
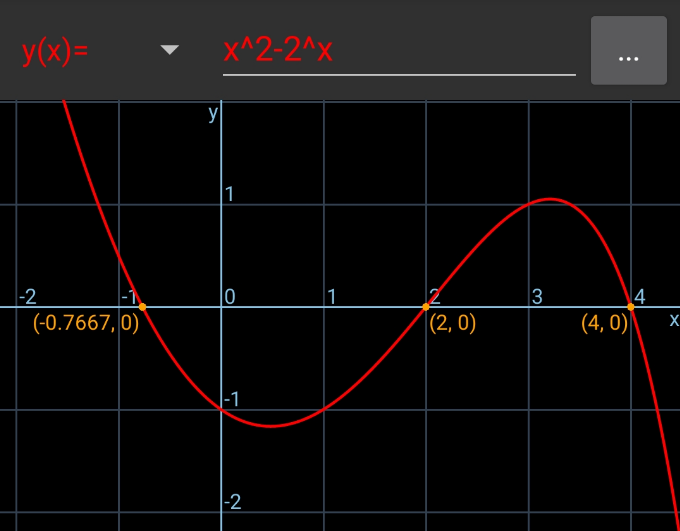
Commented by mr W last updated on 31/May/20
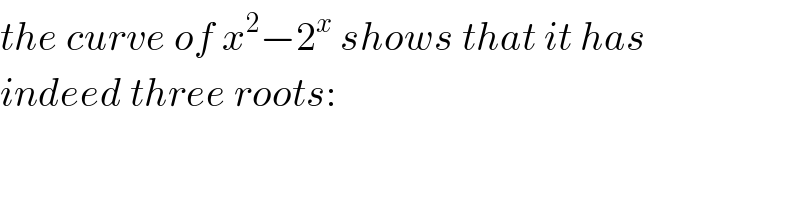
Commented by mr W last updated on 31/May/20