
Question and Answers Forum
Question Number 96282 by 675480065 last updated on 31/May/20
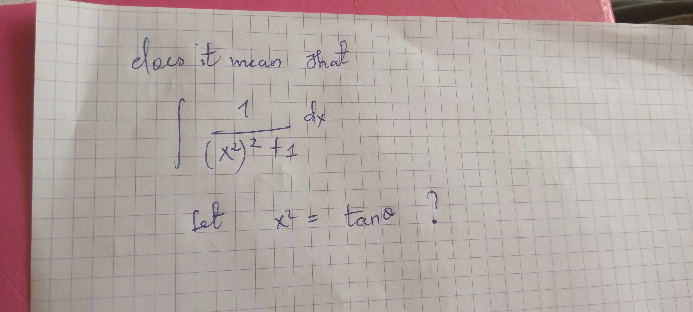
Answered by bemath last updated on 31/May/20

Answered by 1549442205 last updated on 31/May/20
![We have x^4 +1=(x^2 +1)^2 −2x^2 =(x^2 +(√2) x+1)(x^2 −(√2) x+1) Hence,(1/(x^4 +1))=((ax+b)/(x^2 +(√(2 ))x+1))+((cx+d)/(x^2 −(√2)x+1)) ⇔1=(a+c)x^3 +[b+d+(√2)(c−a)]x^2 +[(√2)(c−b)+a+c]x+b+d { ((a+c=0)),((b+d=1)) :} { ((b+d+(√2)(c−a)=0)),(((√2)(c−b)+a+c=0)) :} Deduce a=(1/(2(√2))),b=c=((−1)/(2(√2))),d=1+(1/(2(√2))). hen ∫(dx/(x^4 +1))=(1/(2(√2)))∫((x−1)/(x^2 +(√2)x+1))dx−(1/(2(√2)))∫((x−2(√(2−))1)/(x^2 −(√2)x+1))dx= I=∫((x−1)/(x^2 +(√2)x+1))dx=(1/2)∫((d(x^2 +(√2)x+1))/(x^2 +(√2)x+1))dx+(1/2)∫((−(√2)−2)/(x^2 +(√2)x+1))dx =(1/2)∫((d(x^2 +(√2)x+1))/(x^2 +(√2)x+1))dx−((2+(√2))/2)∫(dx/((x+((√2)/2))^2 +((1/(√2)))^2 )) =(1/2)ln(x^2 +(√2)x+1)−((2+(√2))/2)[((√2)x+1)arctan((√2)x+1)] J=∫((x−2(√2)−1)/(x^2 −(√2)x+1))dx=(1/2)∫((d(x^2 −(√2)x+1))/(x^2 −(√2)x+1))+(1/2)∫((−3(√2)−2)/(x^2 −(√2)x+1))dx =(1/2)ln(x^2 −(√2)x+1)−((3(√2)+2)/2)[((√2)x−1)arctan((√2)x−1) From that F(x)= ∫(dx/(x^4 +1))=(1/(4(√2)))ln(x^2 +(√2)x+1)−((2+(√2))/(4(√2)))[((√2)x+1)arctan((√2)x+1)] −(1/(4(√2)))ln(x^2 −(√2)x+1)+((3(√2)+2)/(4(√2)))[((√2)x−1)arctan((√2)x−1)+C F(x)=(1/(4(√2)))ln((x^2 +(√2)x+1)/(x^2 −(√2)x+1))−(((√2)+1)/4)[((√2)x+1)arctan((√2)x+1)]+((3+(√2))/4)[((√2)x−1)arctan((√2)x−1)]+C](Q96316.png)
Answered by mathmax by abdo last updated on 31/May/20

| ||
Question and Answers Forum | ||
Question Number 96282 by 675480065 last updated on 31/May/20 | ||
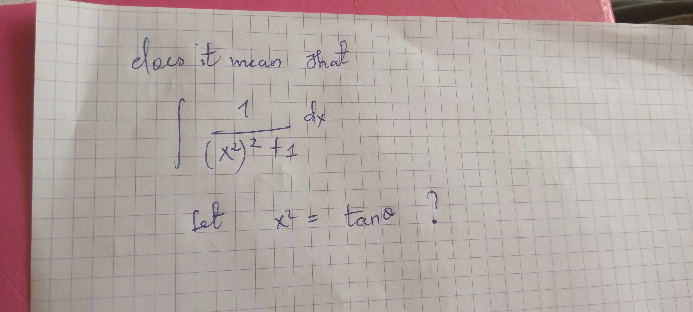 | ||
Answered by bemath last updated on 31/May/20 | ||
 | ||
| ||
Answered by 1549442205 last updated on 31/May/20 | ||
![We have x^4 +1=(x^2 +1)^2 −2x^2 =(x^2 +(√2) x+1)(x^2 −(√2) x+1) Hence,(1/(x^4 +1))=((ax+b)/(x^2 +(√(2 ))x+1))+((cx+d)/(x^2 −(√2)x+1)) ⇔1=(a+c)x^3 +[b+d+(√2)(c−a)]x^2 +[(√2)(c−b)+a+c]x+b+d { ((a+c=0)),((b+d=1)) :} { ((b+d+(√2)(c−a)=0)),(((√2)(c−b)+a+c=0)) :} Deduce a=(1/(2(√2))),b=c=((−1)/(2(√2))),d=1+(1/(2(√2))). hen ∫(dx/(x^4 +1))=(1/(2(√2)))∫((x−1)/(x^2 +(√2)x+1))dx−(1/(2(√2)))∫((x−2(√(2−))1)/(x^2 −(√2)x+1))dx= I=∫((x−1)/(x^2 +(√2)x+1))dx=(1/2)∫((d(x^2 +(√2)x+1))/(x^2 +(√2)x+1))dx+(1/2)∫((−(√2)−2)/(x^2 +(√2)x+1))dx =(1/2)∫((d(x^2 +(√2)x+1))/(x^2 +(√2)x+1))dx−((2+(√2))/2)∫(dx/((x+((√2)/2))^2 +((1/(√2)))^2 )) =(1/2)ln(x^2 +(√2)x+1)−((2+(√2))/2)[((√2)x+1)arctan((√2)x+1)] J=∫((x−2(√2)−1)/(x^2 −(√2)x+1))dx=(1/2)∫((d(x^2 −(√2)x+1))/(x^2 −(√2)x+1))+(1/2)∫((−3(√2)−2)/(x^2 −(√2)x+1))dx =(1/2)ln(x^2 −(√2)x+1)−((3(√2)+2)/2)[((√2)x−1)arctan((√2)x−1) From that F(x)= ∫(dx/(x^4 +1))=(1/(4(√2)))ln(x^2 +(√2)x+1)−((2+(√2))/(4(√2)))[((√2)x+1)arctan((√2)x+1)] −(1/(4(√2)))ln(x^2 −(√2)x+1)+((3(√2)+2)/(4(√2)))[((√2)x−1)arctan((√2)x−1)+C F(x)=(1/(4(√2)))ln((x^2 +(√2)x+1)/(x^2 −(√2)x+1))−(((√2)+1)/4)[((√2)x+1)arctan((√2)x+1)]+((3+(√2))/4)[((√2)x−1)arctan((√2)x−1)]+C](Q96316.png) | ||
| ||
Answered by mathmax by abdo last updated on 31/May/20 | ||
 | ||
| ||