
Question and Answers Forum
Question Number 96373 by mathmax by abdo last updated on 01/Jun/20
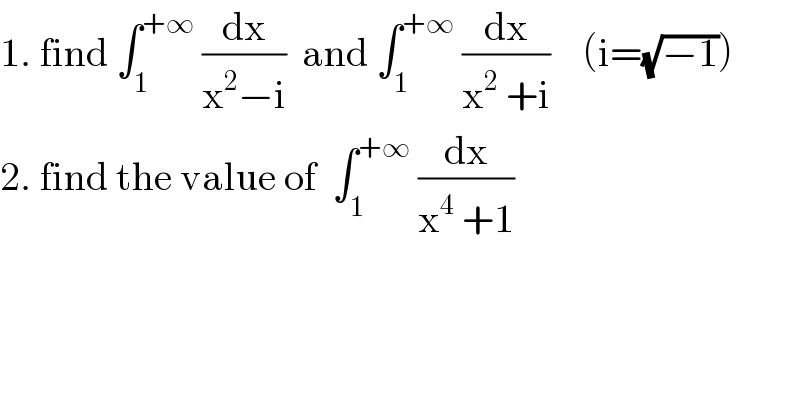
Answered by Sourav mridha last updated on 01/Jun/20
![let I=∫_1 ^(+∞) (dx/(x^2 −i)) and J=∫_1 ^(+∞) (dx/(x^2 +i)) now, I+J=∫_1 ^(+∞) ((2x^2 )/(x^4 +1))dx.....(i) =∫_1 ^(+∞) ((x^2 +1)/(x^4 +1))dx +∫_1 ^∞ ((x^2 −1)/(x^4 +1))dx ........(I_1 ) ..........(I_2 ) =∫_(1 ) ^(+∞) ((d(x−(1/x)))/((x−(1/x))^2 +((√2))^2 )) +∫_1 ^(+∞) ((d(x+(1/x)))/((x+(1/x))^2 −((√2))^2 )) =(1/(√2))[tan^(−1) (((x−(1/x))/(√2)))]_1 ^(+∞) +(1/(2(√2)))[ln(((x+(1/x) −(√2))/(x+(1/x)+(√2))))]_1 ^(+∞) =(𝛑/(2(√2)))−(1/(2(√2)))ln(3−(√2)) now I−J=(1/(2i))∫_1 ^(+∞) (dx/(x^4 +1)) ......(ii) =(1/(4i))[∫_1 ^(+∞) ((x^2 +1)/(x^4 +1))dx−∫_1 ^(+∞) ((x^2 −1)/(x^4 +1))dx] =(1/(4i))[I_1 −I_2 ]=−(i/4)[(𝛑/(2(√2)))+(1/(2(√2)))ln(3−(√2))] now (i)+(ii) I=[(𝛑/(4(√2)))−(1/(4(√2)))ln(3−(√2))]−i[(𝛑/(16(√2)))+(1/(16(√2)))ln(3−(√2))] and (i)−(ii) J=I^∗ =complex conjugate of I. now from (ii)... ∫_1 ^(+∞) (dx/(x^4 +1))=2i(I−J) =[(𝛑/(4(√2)))+(1/(4(√2)))ln(3−(√2))]. very nice problem...it′s really interesting.](Q96399.png)
Commented by abdomathmax last updated on 01/Jun/20

Answered by abdomathmax last updated on 01/Jun/20
![1. ∫_1 ^(+∞) (dx/(x^2 −i)) =∫_1 ^(+∞) (dx/((x−(√i))(x+(√i)))) =(1/(2(√i)))∫_1 ^(+∞) ((1/(x−(√i)))−(1/(x+(√i))))dx =(1/(2(√i)))[ln(((x−(√i))/(x+(√i))))]_1 ^(+∞) =(1/(2(√i)))(−ln(((1−(√i))/(1+(√i))))) =(1/(2(√i)))( ln(1+(√i))−ln(1−(√i))) but 1+(√i)=1+e^((iπ)/4) =1+(1/(√2))+(i/(√2)) =(√((1+(1/(√2)))^2 +(1/2)))× e^(iarctan((1/((√2)(1+(1/(√2)))))) =(√((3/2)+(√2)+(1/2)))e^(iarctan((1/(1+(√2))))) =(√(2+(√2))) e^(iarctan((1/(1+(√2))))) ⇒ ln(1+(√i))=(1/2)ln(2+(√2))+iarctan((1/(1+(√2)))) ln(1−(√i)) =conj(..)=(1/2)ln(2+(√2))−iarctan((1/(1+(√2)))) ⇒(1/(2(√i)))(ln(1+(√i))−ln(1−(√i))) =(1/(2(√i))){2i arctan((1/(1+(√2))))} =(√i)arctan((√2)−1) =(√i)((π/8)) =(π/8)e^((iπ)/4) ∫_1 ^(+∞) (dx/(x^2 +i)) =conj(∫_1 ^(+∞) (dx/(x^2 −i))) =(π/8)e^(−((iπ)/4)) 2.∫_1 ^(+∞) (dx/(x^4 +1)) =∫_1 ^(+∞) (dx/((x^2 −i)(x^2 +i))) =(1/(2i))∫_1 ^(+∞) ((1/(x^2 −i))−(1/(x^2 +i)))dx =(1/(2i))((π/8)e^((iπ)/4) −(π/8)e^(−((iπ)/4)) ) =(π/8)sin((π/4)) =(π/8)×((√2)/2) =((π(√2))/(16))](Q96434.png)
| ||
Question and Answers Forum | ||
Question Number 96373 by mathmax by abdo last updated on 01/Jun/20 | ||
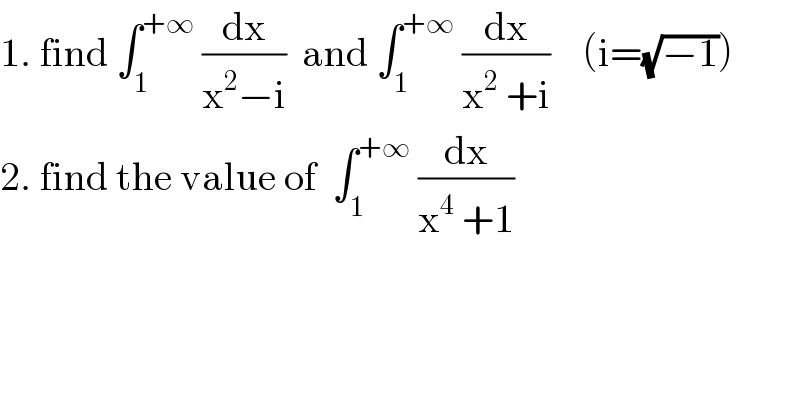 | ||
Answered by Sourav mridha last updated on 01/Jun/20 | ||
![let I=∫_1 ^(+∞) (dx/(x^2 −i)) and J=∫_1 ^(+∞) (dx/(x^2 +i)) now, I+J=∫_1 ^(+∞) ((2x^2 )/(x^4 +1))dx.....(i) =∫_1 ^(+∞) ((x^2 +1)/(x^4 +1))dx +∫_1 ^∞ ((x^2 −1)/(x^4 +1))dx ........(I_1 ) ..........(I_2 ) =∫_(1 ) ^(+∞) ((d(x−(1/x)))/((x−(1/x))^2 +((√2))^2 )) +∫_1 ^(+∞) ((d(x+(1/x)))/((x+(1/x))^2 −((√2))^2 )) =(1/(√2))[tan^(−1) (((x−(1/x))/(√2)))]_1 ^(+∞) +(1/(2(√2)))[ln(((x+(1/x) −(√2))/(x+(1/x)+(√2))))]_1 ^(+∞) =(𝛑/(2(√2)))−(1/(2(√2)))ln(3−(√2)) now I−J=(1/(2i))∫_1 ^(+∞) (dx/(x^4 +1)) ......(ii) =(1/(4i))[∫_1 ^(+∞) ((x^2 +1)/(x^4 +1))dx−∫_1 ^(+∞) ((x^2 −1)/(x^4 +1))dx] =(1/(4i))[I_1 −I_2 ]=−(i/4)[(𝛑/(2(√2)))+(1/(2(√2)))ln(3−(√2))] now (i)+(ii) I=[(𝛑/(4(√2)))−(1/(4(√2)))ln(3−(√2))]−i[(𝛑/(16(√2)))+(1/(16(√2)))ln(3−(√2))] and (i)−(ii) J=I^∗ =complex conjugate of I. now from (ii)... ∫_1 ^(+∞) (dx/(x^4 +1))=2i(I−J) =[(𝛑/(4(√2)))+(1/(4(√2)))ln(3−(√2))]. very nice problem...it′s really interesting.](Q96399.png) | ||
| ||
Commented by abdomathmax last updated on 01/Jun/20 | ||
 | ||
Answered by abdomathmax last updated on 01/Jun/20 | ||
![1. ∫_1 ^(+∞) (dx/(x^2 −i)) =∫_1 ^(+∞) (dx/((x−(√i))(x+(√i)))) =(1/(2(√i)))∫_1 ^(+∞) ((1/(x−(√i)))−(1/(x+(√i))))dx =(1/(2(√i)))[ln(((x−(√i))/(x+(√i))))]_1 ^(+∞) =(1/(2(√i)))(−ln(((1−(√i))/(1+(√i))))) =(1/(2(√i)))( ln(1+(√i))−ln(1−(√i))) but 1+(√i)=1+e^((iπ)/4) =1+(1/(√2))+(i/(√2)) =(√((1+(1/(√2)))^2 +(1/2)))× e^(iarctan((1/((√2)(1+(1/(√2)))))) =(√((3/2)+(√2)+(1/2)))e^(iarctan((1/(1+(√2))))) =(√(2+(√2))) e^(iarctan((1/(1+(√2))))) ⇒ ln(1+(√i))=(1/2)ln(2+(√2))+iarctan((1/(1+(√2)))) ln(1−(√i)) =conj(..)=(1/2)ln(2+(√2))−iarctan((1/(1+(√2)))) ⇒(1/(2(√i)))(ln(1+(√i))−ln(1−(√i))) =(1/(2(√i))){2i arctan((1/(1+(√2))))} =(√i)arctan((√2)−1) =(√i)((π/8)) =(π/8)e^((iπ)/4) ∫_1 ^(+∞) (dx/(x^2 +i)) =conj(∫_1 ^(+∞) (dx/(x^2 −i))) =(π/8)e^(−((iπ)/4)) 2.∫_1 ^(+∞) (dx/(x^4 +1)) =∫_1 ^(+∞) (dx/((x^2 −i)(x^2 +i))) =(1/(2i))∫_1 ^(+∞) ((1/(x^2 −i))−(1/(x^2 +i)))dx =(1/(2i))((π/8)e^((iπ)/4) −(π/8)e^(−((iπ)/4)) ) =(π/8)sin((π/4)) =(π/8)×((√2)/2) =((π(√2))/(16))](Q96434.png) | ||
| ||