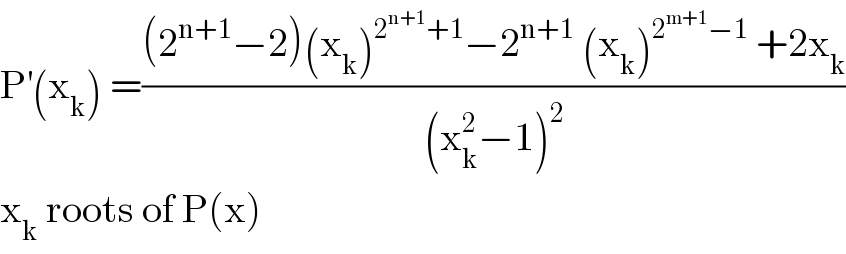Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 96375 by mathmax by abdo last updated on 01/Jun/20

let P(x) =(1+x^2 )(1+x^4 )...(1+x^2^n ) 1) solve inside C the equation P(x)=0 2) factorize P(x) inside C[x] 3) calvulate P^′ (x) 4) decompose F =(1/(P(x)))

$$\mathrm{let}\:\mathrm{P}\left(\mathrm{x}\right)\:=\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)...\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}^{\mathrm{n}} } \right) \\ $$$$\left.\mathrm{1}\right)\:\mathrm{solve}\:\mathrm{inside}\:\mathrm{C}\:\:\mathrm{the}\:\mathrm{equation}\:\mathrm{P}\left(\mathrm{x}\right)=\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{factorize}\:\mathrm{P}\left(\mathrm{x}\right)\:\mathrm{inside}\:\mathrm{C}\left[\mathrm{x}\right] \\ $$$$\left.\mathrm{3}\right)\:\mathrm{calvulate}\:\mathrm{P}^{'} \left(\mathrm{x}\right) \\ $$$$\left.\mathrm{4}\right)\:\mathrm{decompose}\:\mathrm{F}\:=\frac{\mathrm{1}}{\mathrm{P}\left(\mathrm{x}\right)} \\ $$

Answered by 1549442205 last updated on 01/Jun/20

1/P(x)=0⇔x^2^n +1=0(n=1,2,3,...)⇔ x^2^n =−1=[cos(2k+1)π+isin(2k+1)π] ⇒x=[cos(2k+1)π+isin(2k+1)π]^(1/2^n ) =cos(((2k+1)π)/2^n )+i.sin(((2k+1)π)/2^n )(k=0,1,2, ...,2^n −1).It follows that eq.P(x)=0 has 2+4+8+...+2^n =2(2^n −1)roots 2/P(x)=Π_(n=1) ^(2^n ) Π_(k=0) ^(2^n −1) (cos(((2k+1)π)/2^n )+i.sin(((2k+1)π)/2^n )) 3/P(x)=((1−x^(2n+1) )/(1−x^2 ))⇒P ′(x)=((−(2n+1)x^(2n) (1−x^2 )+2x(1−x^(2n+1) ))/((1−x^2 )^2 )) =(((2n−1)x^(2n+2) −(2n+1)x^(2n) +2x)/((1−x^2 )^2 ))

$$\mathrm{1}/\mathrm{P}\left(\mathrm{x}\right)=\mathrm{0}\Leftrightarrow\mathrm{x}^{\mathrm{2}^{\mathrm{n}} } +\mathrm{1}=\mathrm{0}\left(\mathrm{n}=\mathrm{1},\mathrm{2},\mathrm{3},...\right)\Leftrightarrow \\ $$$$\mathrm{x}^{\mathrm{2}^{\mathrm{n}} } =−\mathrm{1}=\left[\mathrm{cos}\left(\mathrm{2k}+\mathrm{1}\right)\pi+\mathrm{isin}\left(\mathrm{2k}+\mathrm{1}\right)\pi\right] \\ $$$$\Rightarrow\mathrm{x}=\left[\mathrm{cos}\left(\mathrm{2k}+\mathrm{1}\right)\pi+\mathrm{isin}\left(\mathrm{2k}+\mathrm{1}\right)\pi\right]^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }} \\ $$$$=\mathrm{cos}\frac{\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{2}^{\mathrm{n}} }+\mathrm{i}.\mathrm{sin}\frac{\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{2}^{\mathrm{n}} }\left(\mathrm{k}=\mathrm{0},\mathrm{1},\mathrm{2},\right. \\ $$$$\left....,\mathrm{2}^{\mathrm{n}} −\mathrm{1}\right).\mathrm{It}\:\mathrm{follows}\:\mathrm{that}\:\mathrm{eq}.\mathrm{P}\left(\mathrm{x}\right)=\mathrm{0}\:\mathrm{has} \\ $$$$\mathrm{2}+\mathrm{4}+\mathrm{8}+...+\mathrm{2}^{\mathrm{n}} =\mathrm{2}\left(\mathrm{2}^{\mathrm{n}} −\mathrm{1}\right)\mathrm{roots} \\ $$$$\mathrm{2}/\mathrm{P}\left(\mathrm{x}\right)=\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{2}^{\mathrm{n}} } {\Pi}}\:\:\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2}^{\mathrm{n}} −\mathrm{1}} {\Pi}}\left(\mathrm{cos}\frac{\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{2}^{\mathrm{n}} }+\mathrm{i}.\mathrm{sin}\frac{\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{2}^{\mathrm{n}} }\right) \\ $$$$\mathrm{3}/\mathrm{P}\left(\mathrm{x}\right)=\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\Rightarrow\mathrm{P}\:'\left(\mathrm{x}\right)=\frac{−\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{2n}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)+\mathrm{2x}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2n}+\mathrm{1}} \right)}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{2n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2n}+\mathrm{2}} −\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{2n}} +\mathrm{2x}}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$ \\ $$

Answered by abdomathmax last updated on 01/Jun/20

1) let prove by recurrence that (1+x^2 )(1+x^4 )....(1+x^2^n ) =((1−x^2^(n+1) )/(1−x^2 )) (x^2 ≠1) n=1 (1+x^2 )=((1−x^4 )/(1−x^2 )) (true) let suppose (p_n )true ⇒(1+x^2 )(1+x^4 )....(1+x^2^(n+1) ) =(1+x^2 )(1+x^4 )....(1+x^2^n )(1+x^2^(n+1) ) =((1−x^2^(n+1) )/(1−x^2 ))×(1+x^2^(n+1) ) =((1−(x^2^(n+1) )^2 )/(1−x^2 )) =((1−x^2^(n+2) )/(1−x^2 )) so the relation is true at term (n+1) ⇒P(x)=0 ⇔((1−x^2^(n+1) )/(1−x^2 )) =0 and x≠+^− 1 ⇒x^2^(n+1) =1 let m =2^(n+1) (e) ⇒x^m =1 =e^(i(2kπ)) ⇒ the roots are z_k =e^(i(((2kπ)/m))) k∈{0,....m−1} ⇒ z_k =e^(i(((kπ)/2^n ))) and k∈{1,....2^(n+1) −1} and k≠2^n

$$\left.\mathrm{1}\right)\:\mathrm{let}\:\mathrm{prove}\:\mathrm{by}\:\mathrm{recurrence}\:\mathrm{that} \\ $$$$\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)....\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}^{\mathrm{n}} } \right)\:=\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}^{\mathrm{n}+\mathrm{1}} } }{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\:\:\:\left(\mathrm{x}^{\mathrm{2}} \:\neq\mathrm{1}\right) \\ $$$$\mathrm{n}=\mathrm{1}\:\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)=\frac{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\left(\mathrm{true}\right)\:\mathrm{let}\:\mathrm{suppose} \\ $$$$\left(\mathrm{p}_{\mathrm{n}} \right)\mathrm{true}\:\Rightarrow\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)....\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}^{\mathrm{n}+\mathrm{1}} } \right) \\ $$$$=\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)....\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}^{\mathrm{n}} } \right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}^{\mathrm{n}+\mathrm{1}} } \right) \\ $$$$=\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}^{\mathrm{n}+\mathrm{1}} } }{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }×\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}^{\mathrm{n}+\mathrm{1}} } \right)\:=\frac{\mathrm{1}−\left(\mathrm{x}^{\mathrm{2}^{\mathrm{n}+\mathrm{1}} } \right)^{\mathrm{2}} }{\mathrm{1}−\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}^{\mathrm{n}+\mathrm{2}} } }{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\:\mathrm{so}\:\mathrm{the}\:\mathrm{relation}\:\mathrm{is}\:\mathrm{true}\:\mathrm{at}\:\mathrm{term}\:\left(\mathrm{n}+\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{P}\left(\mathrm{x}\right)=\mathrm{0}\:\Leftrightarrow\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}^{\mathrm{n}+\mathrm{1}} } }{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:=\mathrm{0}\:\:\mathrm{and}\:\mathrm{x}\neq\overset{−} {+}\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}^{\mathrm{n}+\mathrm{1}} } =\mathrm{1}\:\:\:\mathrm{let}\:\:\mathrm{m}\:=\mathrm{2}^{\mathrm{n}+\mathrm{1}} \:\:\left(\mathrm{e}\right)\:\Rightarrow\mathrm{x}^{\mathrm{m}} \:=\mathrm{1}\:=\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}\pi\right)} \:\Rightarrow \\ $$$$\mathrm{the}\:\mathrm{roots}\:\mathrm{are}\:\mathrm{z}_{\mathrm{k}} =\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{2k}\pi}{\mathrm{m}}\right)} \:\mathrm{k}\in\left\{\mathrm{0},....\mathrm{m}−\mathrm{1}\right\}\:\Rightarrow \\ $$$$\mathrm{z}_{\mathrm{k}} =\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{k}\pi}{\mathrm{2}^{\mathrm{n}} }\right)} \:\:\mathrm{and}\:\mathrm{k}\in\left\{\mathrm{1},....\mathrm{2}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}\right\}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{2}^{\mathrm{n}} \\ $$

Commented by abdomathmax last updated on 01/Jun/20

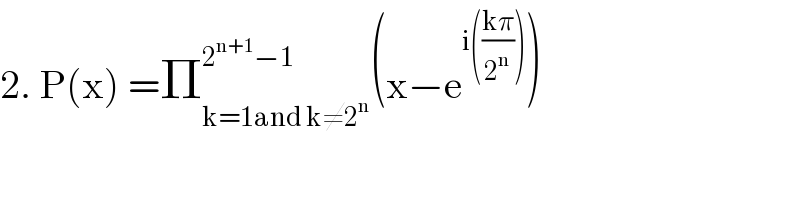
2. P(x) =Π_(k=1and k≠2^n ) ^(2^(n+1) −1) (x−e^(i(((kπ)/2^n ))) )

$$\mathrm{2}.\:\mathrm{P}\left(\mathrm{x}\right)\:=\prod_{\mathrm{k}=\mathrm{1and}\:\mathrm{k}\neq\mathrm{2}^{\mathrm{n}} } ^{\mathrm{2}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}} \left(\mathrm{x}−\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{k}\pi}{\mathrm{2}^{\mathrm{n}} }\right)} \right) \\ $$$$ \\ $$

Commented by abdomathmax last updated on 01/Jun/20

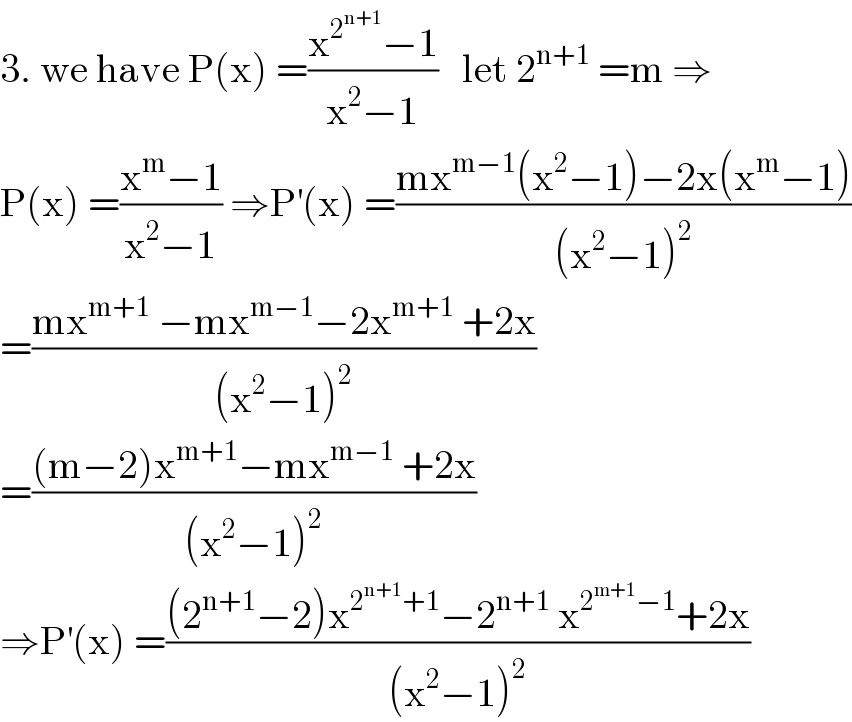
3. we have P(x) =((x^2^(n+1) −1)/(x^2 −1)) let 2^(n+1) =m ⇒ P(x) =((x^m −1)/(x^2 −1)) ⇒P^′ (x) =((mx^(m−1) (x^2 −1)−2x(x^m −1))/((x^2 −1)^2 )) =((mx^(m+1) −mx^(m−1) −2x^(m+1) +2x)/((x^2 −1)^2 )) =(((m−2)x^(m+1) −mx^(m−1) +2x)/((x^2 −1)^2 )) ⇒P^′ (x) =(((2^(n+1) −2)x^(2^(n+1) +1) −2^(n+1) x^(2^(m+1) −1) +2x)/((x^2 −1)^2 ))

$$\mathrm{3}.\:\mathrm{we}\:\mathrm{have}\:\mathrm{P}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}^{\mathrm{2}^{\mathrm{n}+\mathrm{1}} } −\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:\:\:\mathrm{let}\:\mathrm{2}^{\mathrm{n}+\mathrm{1}} \:=\mathrm{m}\:\Rightarrow \\ $$$$\mathrm{P}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}^{\mathrm{m}} −\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:\Rightarrow\mathrm{P}^{'} \left(\mathrm{x}\right)\:=\frac{\mathrm{mx}^{\mathrm{m}−\mathrm{1}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{2x}\left(\mathrm{x}^{\mathrm{m}} −\mathrm{1}\right)}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{mx}^{\mathrm{m}+\mathrm{1}} \:−\mathrm{mx}^{\mathrm{m}−\mathrm{1}} −\mathrm{2x}^{\mathrm{m}+\mathrm{1}} \:+\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{m}−\mathrm{2}\right)\mathrm{x}^{\mathrm{m}+\mathrm{1}} −\mathrm{mx}^{\mathrm{m}−\mathrm{1}} \:+\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{P}^{'} \left(\mathrm{x}\right)\:=\frac{\left(\mathrm{2}^{\mathrm{n}+\mathrm{1}} −\mathrm{2}\right)\mathrm{x}^{\mathrm{2}^{\mathrm{n}+\mathrm{1}} +\mathrm{1}} −\mathrm{2}^{\mathrm{n}+\mathrm{1}} \:\mathrm{x}^{\mathrm{2}^{\mathrm{m}+\mathrm{1}} −\mathrm{1}} +\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Commented by abdomathmax last updated on 01/Jun/20

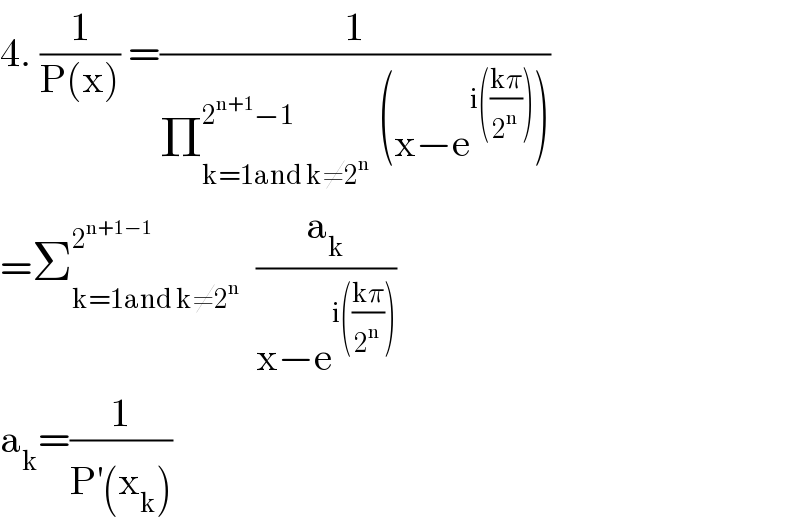
4. (1/(P(x))) =(1/(Π_(k=1and k≠2^n ) ^(2^(n+1) −1) (x−e^(i(((kπ)/2^n ))) ))) =Σ_(k=1and k≠2^n ) ^(2^(n+1−1) ) (a_k /(x−e^(i(((kπ)/2^n ))) )) a_k =(1/(P^′ (x_k )))

$$\mathrm{4}.\:\frac{\mathrm{1}}{\mathrm{P}\left(\mathrm{x}\right)}\:=\frac{\mathrm{1}}{\prod_{\mathrm{k}=\mathrm{1and}\:\mathrm{k}\neq\mathrm{2}^{\mathrm{n}} } ^{\mathrm{2}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}} \:\left(\mathrm{x}−\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{k}\pi}{\mathrm{2}^{\mathrm{n}} }\right)} \right)} \\ $$$$=\sum_{\mathrm{k}=\mathrm{1and}\:\mathrm{k}\neq\mathrm{2}^{\mathrm{n}} } ^{\mathrm{2}^{\mathrm{n}+\mathrm{1}−\mathrm{1}} \:} \:\:\frac{\mathrm{a}_{\mathrm{k}} }{\mathrm{x}−\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{k}\pi}{\mathrm{2}^{\mathrm{n}} }\right)} } \\ $$$$\mathrm{a}_{\mathrm{k}} =\frac{\mathrm{1}}{\mathrm{P}^{'} \left(\mathrm{x}_{\mathrm{k}} \right)} \\ $$

Commented by abdomathmax last updated on 01/Jun/20

P^′ (x_k ) =(((2^(n+1) −2)(x_k )^(2^(n+1) +1) −2^(n+1) (x_k )^(2^(m+1) −1) +2x_k )/((x_k ^2 −1)^2 )) x_k roots of P(x)

$$\mathrm{P}^{'} \left(\mathrm{x}_{\mathrm{k}} \right)\:=\frac{\left(\mathrm{2}^{\mathrm{n}+\mathrm{1}} −\mathrm{2}\right)\left(\mathrm{x}_{\mathrm{k}} \right)^{\mathrm{2}^{\mathrm{n}+\mathrm{1}} +\mathrm{1}} −\mathrm{2}^{\mathrm{n}+\mathrm{1}} \:\left(\mathrm{x}_{\mathrm{k}} \right)^{\mathrm{2}^{\mathrm{m}+\mathrm{1}} −\mathrm{1}} \:+\mathrm{2x}_{\mathrm{k}} }{\left(\mathrm{x}_{\mathrm{k}} ^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{x}_{\mathrm{k}} \:\mathrm{roots}\:\mathrm{of}\:\mathrm{P}\left(\mathrm{x}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com