Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 96419 by Hassanfathi last updated on 01/Jun/20

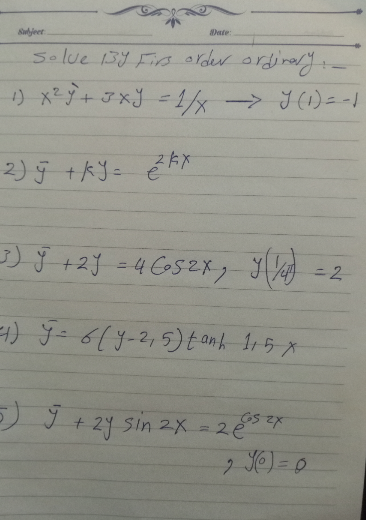
Commented by bemath last updated on 01/Jun/20

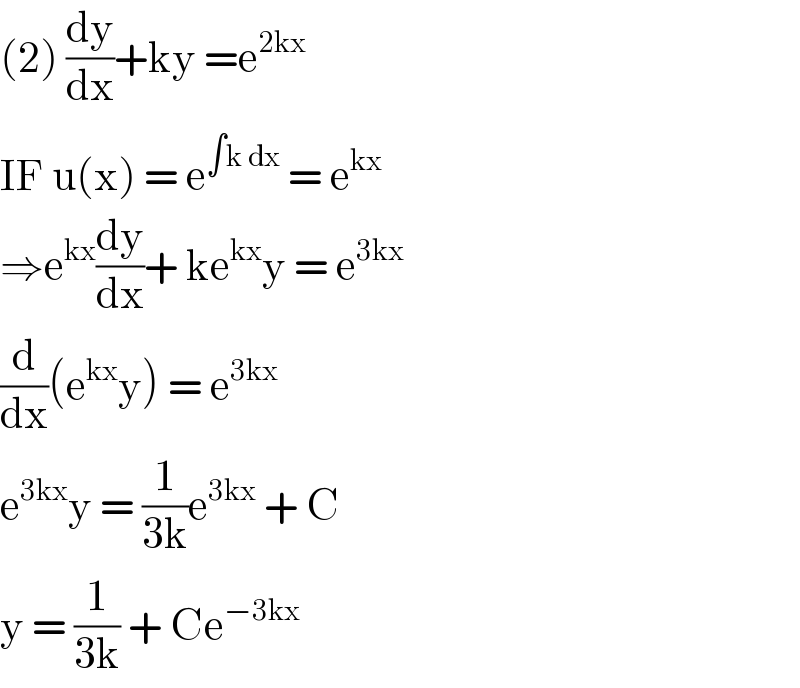
(2) (dy/dx)+ky =e^(2kx) IF u(x) = e^(∫k dx) = e^(kx) ⇒e^(kx) (dy/dx)+ ke^(kx) y = e^(3kx) (d/dx)(e^(kx) y) = e^(3kx) e^(3kx) y = (1/(3k))e^(3kx) + C y = (1/(3k)) + Ce^(−3kx)

$$\left(\mathrm{2}\right)\:\frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{ky}\:=\mathrm{e}^{\mathrm{2kx}} \\ $$$$\mathrm{IF}\:\mathrm{u}\left(\mathrm{x}\right)\:=\:\mathrm{e}^{\int\mathrm{k}\:\mathrm{dx}} \:=\:\mathrm{e}^{\mathrm{kx}} \\ $$$$\Rightarrow\mathrm{e}^{\mathrm{kx}} \frac{\mathrm{dy}}{\mathrm{dx}}+\:\mathrm{ke}^{\mathrm{kx}} \mathrm{y}\:=\:\mathrm{e}^{\mathrm{3kx}} \\ $$$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{e}^{\mathrm{kx}} \mathrm{y}\right)\:=\:\mathrm{e}^{\mathrm{3kx}} \\ $$$$\mathrm{e}^{\mathrm{3kx}} \mathrm{y}\:=\:\frac{\mathrm{1}}{\mathrm{3k}}\mathrm{e}^{\mathrm{3kx}} \:+\:\mathrm{C}\: \\ $$$$\mathrm{y}\:=\:\frac{\mathrm{1}}{\mathrm{3k}}\:+\:\mathrm{Ce}^{−\mathrm{3kx}} \: \\ $$

Commented by bemath last updated on 01/Jun/20

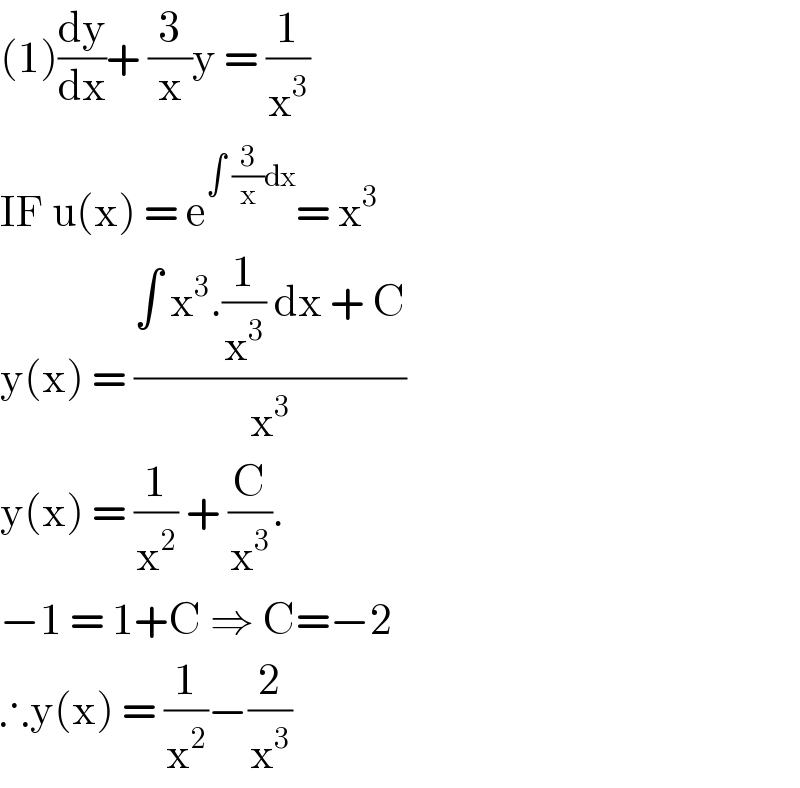
(1)(dy/dx)+ (3/x)y = (1/x^3 ) IF u(x) = e^(∫ (3/x)dx) = x^3 y(x) = ((∫ x^3 .(1/x^3 ) dx + C)/x^3 ) y(x) = (1/x^2 ) + (C/x^3 ). −1 = 1+C ⇒ C=−2 ∴y(x) = (1/x^2 )−(2/x^3 )

$$\left(\mathrm{1}\right)\frac{\mathrm{dy}}{\mathrm{dx}}+\:\frac{\mathrm{3}}{\mathrm{x}}\mathrm{y}\:=\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\: \\ $$$$\mathrm{IF}\:\mathrm{u}\left(\mathrm{x}\right)\:=\:\mathrm{e}^{\int\:\frac{\mathrm{3}}{\mathrm{x}}\mathrm{dx}} =\:\mathrm{x}^{\mathrm{3}} \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\:\frac{\int\:\mathrm{x}^{\mathrm{3}} .\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\:\mathrm{dx}\:+\:\mathrm{C}}{\mathrm{x}^{\mathrm{3}} } \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:+\:\frac{\mathrm{C}}{\mathrm{x}^{\mathrm{3}} }. \\ $$$$−\mathrm{1}\:=\:\mathrm{1}+\mathrm{C}\:\Rightarrow\:\mathrm{C}=−\mathrm{2} \\ $$$$\therefore\mathrm{y}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{3}} } \\ $$

Commented by john santu last updated on 01/Jun/20

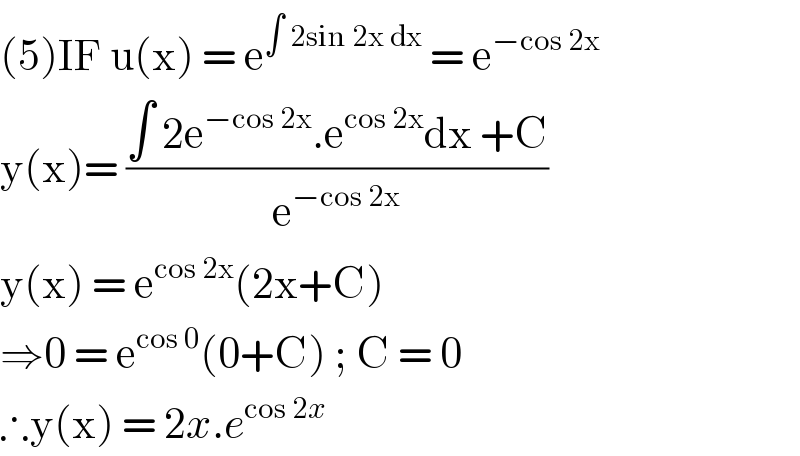
(5)IF u(x) = e^(∫ 2sin 2x dx) = e^(−cos 2x) y(x)= ((∫ 2e^(−cos 2x) .e^(cos 2x) dx +C)/e^(−cos 2x) ) y(x) = e^(cos 2x) (2x+C) ⇒0 = e^(cos 0) (0+C) ; C = 0 ∴y(x) = 2x.e^(cos 2x)

$$\left(\mathrm{5}\right)\mathrm{IF}\:\mathrm{u}\left(\mathrm{x}\right)\:=\:\mathrm{e}^{\int\:\mathrm{2sin}\:\mathrm{2x}\:\mathrm{dx}} \:=\:\mathrm{e}^{−\mathrm{cos}\:\mathrm{2x}} \\ $$$$\mathrm{y}\left(\mathrm{x}\right)=\:\frac{\int\:\mathrm{2e}^{−\mathrm{cos}\:\mathrm{2x}} .\mathrm{e}^{\mathrm{cos}\:\mathrm{2x}} \mathrm{dx}\:+\mathrm{C}}{\mathrm{e}^{−\mathrm{cos}\:\mathrm{2x}} } \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\:\mathrm{e}^{\mathrm{cos}\:\mathrm{2x}} \left(\mathrm{2x}+\mathrm{C}\right) \\ $$$$\Rightarrow\mathrm{0}\:=\:\mathrm{e}^{\mathrm{cos}\:\mathrm{0}} \left(\mathrm{0}+\mathrm{C}\right)\:;\:\mathrm{C}\:=\:\mathrm{0} \\ $$$$\therefore\mathrm{y}\left(\mathrm{x}\right)\:=\:\mathrm{2}{x}.{e}^{\mathrm{cos}\:\mathrm{2}{x}} \: \\ $$

Answered by mathmax by abdo last updated on 01/Jun/20

3) y^′ +2y =4cos(2x) and y((π/4))=2 (he)→y^′ +2y =0 ⇒(y^′ /y) =−2 ⇒ln∣y∣ =−2x +c ⇒y =ke^(−2x) mvc method→y^′ =k^′ e^(−2x) −2k e^(−2x) (e)⇒k^′ e^(−2x) −2ke^(−2x) +2k e^(−2x) =4 cos(2x) ⇒k^′ =4e^(2x) cos(2x) ⇒ k =4 ∫ e^(2x) cos(2x)dx +λ we have ∫ e^(2x) cos(2x)dx=Re(∫ e^(2x+2ix) dx) ∫ e^((2+2i)x) dx =(1/(2+2i))e^((2+2i)x) +c =((2−2i)/8) e^(2x) (cos(2x)+isin(2x)) =((1−i)/4)e^(2x) (cos(2x)+isin(2x)) =(e^(2x) /4)(1−i)(cos(2x)+isin(2x)) =(e^(2x) /4){ cos(2x)+isin(2x)−icos(2x)+sin(2x)) ⇒ ∫ e^(2x) cos(2x)dx =(e^(2x) /4)( cos(2x)+sin(2x)) ⇒ k(x) =e^(2x) (cos(2x)+sin(2x)) +λ ⇒y(x) =k(x)e^(−2x) y(x) =e^(−2x) (e^(2x) (cos(2x)+sin(2x))+λ) =λe^(−2x) +cos(2x)+sin(2x) y((π/4))=2 ⇒λ e^(−(π/2)) +1 =2 ⇒λe^(−(π/2)) =1 ⇒λ =e^(π/2) ⇒ y(x) =e^((π/2)−2x) +cos(2x) +sin(2x)

$$\left.\mathrm{3}\right)\:\mathrm{y}^{'} \:+\mathrm{2y}\:=\mathrm{4cos}\left(\mathrm{2x}\right)\:\mathrm{and}\:\mathrm{y}\left(\frac{\pi}{\mathrm{4}}\right)=\mathrm{2} \\ $$$$\left(\mathrm{he}\right)\rightarrow\mathrm{y}^{'} \:+\mathrm{2y}\:=\mathrm{0}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}\:=−\mathrm{2}\:\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid\:=−\mathrm{2x}\:+\mathrm{c}\:\Rightarrow\mathrm{y}\:=\mathrm{ke}^{−\mathrm{2x}} \\ $$$$\mathrm{mvc}\:\mathrm{method}\rightarrow\mathrm{y}^{'} \:=\mathrm{k}^{'} \:\mathrm{e}^{−\mathrm{2x}} \:−\mathrm{2k}\:\mathrm{e}^{−\mathrm{2x}} \\ $$$$\left(\mathrm{e}\right)\Rightarrow\mathrm{k}^{'} \:\mathrm{e}^{−\mathrm{2x}} −\mathrm{2ke}^{−\mathrm{2x}} \:+\mathrm{2k}\:\mathrm{e}^{−\mathrm{2x}} \:=\mathrm{4}\:\mathrm{cos}\left(\mathrm{2x}\right)\:\Rightarrow\mathrm{k}^{'} \:=\mathrm{4e}^{\mathrm{2x}} \:\mathrm{cos}\left(\mathrm{2x}\right)\:\Rightarrow \\ $$$$\mathrm{k}\:=\mathrm{4}\:\int\:\:\mathrm{e}^{\mathrm{2x}} \:\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{dx}\:+\lambda\:\:\mathrm{we}\:\mathrm{have}\:\int\:\mathrm{e}^{\mathrm{2x}} \:\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{dx}=\mathrm{Re}\left(\int\:\mathrm{e}^{\mathrm{2x}+\mathrm{2ix}} \:\mathrm{dx}\right) \\ $$$$\int\:\:\mathrm{e}^{\left(\mathrm{2}+\mathrm{2i}\right)\mathrm{x}} \:\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}+\mathrm{2i}}\mathrm{e}^{\left(\mathrm{2}+\mathrm{2i}\right)\mathrm{x}} \:+\mathrm{c}\:=\frac{\mathrm{2}−\mathrm{2i}}{\mathrm{8}}\:\:\mathrm{e}^{\mathrm{2x}} \left(\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{isin}\left(\mathrm{2x}\right)\right) \\ $$$$=\frac{\mathrm{1}−\mathrm{i}}{\mathrm{4}}\mathrm{e}^{\mathrm{2x}} \left(\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{isin}\left(\mathrm{2x}\right)\right)\:=\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{4}}\left(\mathrm{1}−\mathrm{i}\right)\left(\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{isin}\left(\mathrm{2x}\right)\right) \\ $$$$=\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{4}}\left\{\:\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{isin}\left(\mathrm{2x}\right)−\mathrm{icos}\left(\mathrm{2x}\right)+\mathrm{sin}\left(\mathrm{2x}\right)\right)\:\Rightarrow \\ $$$$\int\:\mathrm{e}^{\mathrm{2x}} \:\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{dx}\:=\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{4}}\left(\:\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{sin}\left(\mathrm{2x}\right)\right)\:\Rightarrow \\ $$$$\mathrm{k}\left(\mathrm{x}\right)\:=\mathrm{e}^{\mathrm{2x}} \left(\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{sin}\left(\mathrm{2x}\right)\right)\:+\lambda\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{k}\left(\mathrm{x}\right)\mathrm{e}^{−\mathrm{2x}} \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{e}^{−\mathrm{2x}} \left(\mathrm{e}^{\mathrm{2x}} \left(\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{sin}\left(\mathrm{2x}\right)\right)+\lambda\right)\:=\lambda\mathrm{e}^{−\mathrm{2x}} \:+\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{sin}\left(\mathrm{2x}\right) \\ $$$$\mathrm{y}\left(\frac{\pi}{\mathrm{4}}\right)=\mathrm{2}\:\Rightarrow\lambda\:\mathrm{e}^{−\frac{\pi}{\mathrm{2}}} \:+\mathrm{1}\:=\mathrm{2}\:\Rightarrow\lambda\mathrm{e}^{−\frac{\pi}{\mathrm{2}}} \:=\mathrm{1}\:\Rightarrow\lambda\:=\mathrm{e}^{\frac{\pi}{\mathrm{2}}} \:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\pi}{\mathrm{2}}−\mathrm{2x}} \:+\mathrm{cos}\left(\mathrm{2x}\right)\:+\mathrm{sin}\left(\mathrm{2x}\right) \\ $$

Answered by mathmax by abdo last updated on 01/Jun/20

1) x^2 y^′ +3xy =(1/x) and y(1)=−1 (e)⇒y^′ +(3/x)y =(1/x^3 ) (he)→y^′ +(3/x)y =0 ⇒y^′ =−(3/x)y ⇒(y^′ /y) =−(3/x) ⇒ln∣y∣ =−3ln∣x∣ +c ⇒ y =(k/(∣x∣^3 )) solution on ]0,+∞[ ⇒y =k x^(−3) ⇒y^′ =k^′ x^(−3) −3k x^(−4) (e) ⇒k^′ x^(−3) −3k x^(−4) +(3/x)kx^(−3) =(1/x^3 ) ⇒k^′ x^(−3) =(1/x^3 ) ⇒k^′ =1 ⇒k(x) =x +λ y(x) =(x+λ)x^(−3) =(1/x^2 ) +(λ/x^3 ) y(1) =−1 ⇒1+λ =−1 ⇒λ =−2 ⇒y(x) =(1/x^2 )−(2/x^3 )

$$\left.\mathrm{1}\right)\:\:\mathrm{x}^{\mathrm{2}} \mathrm{y}^{'} \:+\mathrm{3xy}\:=\frac{\mathrm{1}}{\mathrm{x}}\:\:\mathrm{and}\:\mathrm{y}\left(\mathrm{1}\right)=−\mathrm{1} \\ $$$$\left(\mathrm{e}\right)\Rightarrow\mathrm{y}^{'} \:+\frac{\mathrm{3}}{\mathrm{x}}\mathrm{y}\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} } \\ $$$$\left(\mathrm{he}\right)\rightarrow\mathrm{y}^{'} \:+\frac{\mathrm{3}}{\mathrm{x}}\mathrm{y}\:=\mathrm{0}\:\Rightarrow\mathrm{y}^{'} \:=−\frac{\mathrm{3}}{\mathrm{x}}\mathrm{y}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}\:=−\frac{\mathrm{3}}{\mathrm{x}}\:\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid\:=−\mathrm{3ln}\mid\mathrm{x}\mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\left.\mathrm{y}\:=\frac{\mathrm{k}}{\mid\mathrm{x}\mid^{\mathrm{3}} }\:\:\mathrm{solution}\:\mathrm{on}\:\right]\mathrm{0},+\infty\left[\:\Rightarrow\mathrm{y}\:=\mathrm{k}\:\mathrm{x}^{−\mathrm{3}} \:\Rightarrow\mathrm{y}^{'} \:=\mathrm{k}^{'} \:\mathrm{x}^{−\mathrm{3}} \:−\mathrm{3k}\:\mathrm{x}^{−\mathrm{4}} \right. \\ $$$$\left(\mathrm{e}\right)\:\Rightarrow\mathrm{k}^{'} \:\mathrm{x}^{−\mathrm{3}} \:−\mathrm{3k}\:\mathrm{x}^{−\mathrm{4}} \:+\frac{\mathrm{3}}{\mathrm{x}}\mathrm{kx}^{−\mathrm{3}} \:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\:\Rightarrow\mathrm{k}^{'} \:\mathrm{x}^{−\mathrm{3}} \:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\:\Rightarrow\mathrm{k}^{'} \:=\mathrm{1}\:\Rightarrow\mathrm{k}\left(\mathrm{x}\right)\:=\mathrm{x}\:+\lambda \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\left(\mathrm{x}+\lambda\right)\mathrm{x}^{−\mathrm{3}} \:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:+\frac{\lambda}{\mathrm{x}^{\mathrm{3}} } \\ $$$$\mathrm{y}\left(\mathrm{1}\right)\:=−\mathrm{1}\:\Rightarrow\mathrm{1}+\lambda\:=−\mathrm{1}\:\Rightarrow\lambda\:=−\mathrm{2}\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{3}} } \\ $$$$ \\ $$

Answered by Sourav mridha last updated on 01/Jun/20

(5) (dy/dx)+2ysin2x=2e^(cos2x) ⇒muli:by e^(−cos2x) and integrating bothsides ⇒∫d(ye^(−cos2x) )=2∫dx ⇒ye^(−cos2x) =2x+c using the boundary condition y(0)=0 ⇒(0)e^(−1) =2.(0)+c;so c=0 Final sol^n :y=2xe^(cos2x) .

$$\left(\mathrm{5}\right)\:\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}+\mathrm{2}\boldsymbol{{ysin}}\mathrm{2}\boldsymbol{{x}}=\mathrm{2}\boldsymbol{{e}}^{\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{x}}} \\ $$$$\Rightarrow\boldsymbol{{muli}}:\boldsymbol{{by}}\:\boldsymbol{{e}}^{−\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{x}}} \:\boldsymbol{{and}}\:\boldsymbol{{integrating}}\:\boldsymbol{{bothsides}} \\ $$$$\Rightarrow\int\boldsymbol{{d}}\left(\boldsymbol{{ye}}^{−\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{x}}} \right)=\mathrm{2}\int\boldsymbol{{dx}} \\ $$$$\Rightarrow\boldsymbol{{ye}}^{−\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{x}}} =\mathrm{2}\boldsymbol{{x}}+\boldsymbol{{c}} \\ $$$$\boldsymbol{{using}}\:\boldsymbol{{the}}\:\boldsymbol{{bound}}\mathrm{ary}\:\boldsymbol{{condition}} \\ $$$$\boldsymbol{{y}}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{0}\right)\boldsymbol{{e}}^{−\mathrm{1}} =\mathrm{2}.\left(\mathrm{0}\right)+\boldsymbol{{c}};\boldsymbol{{so}}\:\boldsymbol{{c}}=\mathrm{0} \\ $$$$\boldsymbol{{F}}\mathrm{i}\boldsymbol{{nal}}\:\boldsymbol{{sol}}^{\boldsymbol{{n}}} :\boldsymbol{{y}}=\mathrm{2}\boldsymbol{{xe}}^{\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{x}}} . \\ $$$$ \\ $$

Answered by Sourav mridha last updated on 01/Jun/20

(dy/dx)+2y=4cos2x mult:by e^(2x) and inte:bothsides ∫d(ye^(2x) )=4Re[∫e^(2(1+i)x) dx] ⇒ye^(2x) =4Re[(cos2x+isin2x)(e^(2x) /(2(1+i)))] =Re[e^(2x) (cos2x+isin2x).(1−i)] y =(cos2x+sin2x)+c.e^(−2x) given y((𝛑/4))=2;so ⇒2=0+1+c.e^(−(𝛑/2)) ⇒c=e^(𝛑/2) final sol^n : y=(cos2x+sin2x)+e^((𝛑/2)−2x)

$$\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}+\mathrm{2}\boldsymbol{{y}}=\mathrm{4}\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{x}} \\ $$$$\boldsymbol{{mult}}:\boldsymbol{{by}}\:\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{x}}} \boldsymbol{{and}}\:\boldsymbol{{inte}}:\boldsymbol{{bothsides}} \\ $$$$\int\boldsymbol{{d}}\left(\boldsymbol{{ye}}^{\mathrm{2}\boldsymbol{{x}}} \right)=\mathrm{4}\boldsymbol{{Re}}\left[\int\boldsymbol{{e}}^{\mathrm{2}\left(\mathrm{1}+\boldsymbol{{i}}\right)\boldsymbol{{x}}} \boldsymbol{{dx}}\right] \\ $$$$\Rightarrow\boldsymbol{{ye}}^{\mathrm{2}\boldsymbol{{x}}} =\mathrm{4}\boldsymbol{{Re}}\left[\left(\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{x}}+\boldsymbol{{isin}}\mathrm{2}\boldsymbol{{x}}\right)\frac{\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{x}}} }{\mathrm{2}\left(\mathrm{1}+\boldsymbol{{i}}\right)}\right] \\ $$$$\:\:\:\:\:\:\:=\boldsymbol{{R}}\mathrm{e}\left[\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{x}}} \left(\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{x}}+\boldsymbol{{isin}}\mathrm{2}\boldsymbol{{x}}\right).\left(\mathrm{1}−\boldsymbol{{i}}\right)\right] \\ $$$$\:\:\boldsymbol{{y}}\:\:\:\:\:=\left(\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{x}}+\boldsymbol{{sin}}\mathrm{2}\boldsymbol{{x}}\right)+\boldsymbol{{c}}.\boldsymbol{{e}}^{−\mathrm{2}\boldsymbol{{x}}} \\ $$$$\boldsymbol{{given}}\:\boldsymbol{{y}}\left(\frac{\boldsymbol{\pi}}{\mathrm{4}}\right)=\mathrm{2};\boldsymbol{{so}} \\ $$$$\Rightarrow\mathrm{2}=\mathrm{0}+\mathrm{1}+\boldsymbol{{c}}.\boldsymbol{{e}}^{−\frac{\boldsymbol{\pi}}{\mathrm{2}}} \Rightarrow\boldsymbol{{c}}=\boldsymbol{{e}}^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \\ $$$$\boldsymbol{{final}}\:\boldsymbol{{sol}}^{\boldsymbol{{n}}} : \\ $$$$\boldsymbol{{y}}=\left(\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{x}}+\boldsymbol{{sin}}\mathrm{2}\boldsymbol{{x}}\right)+\boldsymbol{{e}}^{\frac{\boldsymbol{\pi}}{\mathrm{2}}−\mathrm{2}\boldsymbol{{x}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Answered by abdomathmax last updated on 01/Jun/20

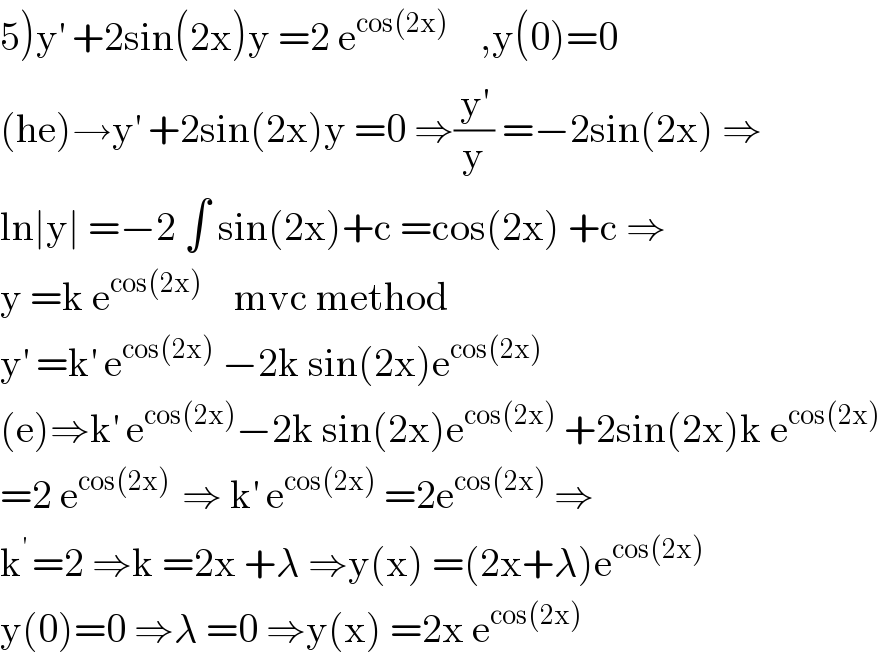
5)y^′ +2sin(2x)y =2 e^(cos(2x)) ,y(0)=0 (he)→y^′ +2sin(2x)y =0 ⇒(y^′ /y) =−2sin(2x) ⇒ ln∣y∣ =−2 ∫ sin(2x)+c =cos(2x) +c ⇒ y =k e^(cos(2x)) mvc method y^′ =k^′ e^(cos(2x)) −2k sin(2x)e^(cos(2x)) (e)⇒k^′ e^(cos(2x)) −2k sin(2x)e^(cos(2x)) +2sin(2x)k e^(cos(2x)) =2 e^(cos(2x) ) ⇒ k^′ e^(cos(2x)) =2e^(cos(2x)) ⇒ k^(′ ) =2 ⇒k =2x +λ ⇒y(x) =(2x+λ)e^(cos(2x)) y(0)=0 ⇒λ =0 ⇒y(x) =2x e^(cos(2x))

$$\left.\mathrm{5}\right)\mathrm{y}^{'} \:+\mathrm{2sin}\left(\mathrm{2x}\right)\mathrm{y}\:=\mathrm{2}\:\mathrm{e}^{\mathrm{cos}\left(\mathrm{2x}\right)} \:\:\:\:,\mathrm{y}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\left(\mathrm{he}\right)\rightarrow\mathrm{y}^{'} \:+\mathrm{2sin}\left(\mathrm{2x}\right)\mathrm{y}\:=\mathrm{0}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}\:=−\mathrm{2sin}\left(\mathrm{2x}\right)\:\Rightarrow \\ $$$$\mathrm{ln}\mid\mathrm{y}\mid\:=−\mathrm{2}\:\int\:\mathrm{sin}\left(\mathrm{2x}\right)+\mathrm{c}\:=\mathrm{cos}\left(\mathrm{2x}\right)\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\:=\mathrm{k}\:\mathrm{e}^{\mathrm{cos}\left(\mathrm{2x}\right)} \:\:\:\:\mathrm{mvc}\:\mathrm{method} \\ $$$$\mathrm{y}^{'} \:=\mathrm{k}^{'} \:\mathrm{e}^{\mathrm{cos}\left(\mathrm{2x}\right)} \:−\mathrm{2k}\:\mathrm{sin}\left(\mathrm{2x}\right)\mathrm{e}^{\mathrm{cos}\left(\mathrm{2x}\right)} \\ $$$$\left(\mathrm{e}\right)\Rightarrow\mathrm{k}^{'} \:\mathrm{e}^{\mathrm{cos}\left(\mathrm{2x}\right)} −\mathrm{2k}\:\mathrm{sin}\left(\mathrm{2x}\right)\mathrm{e}^{\mathrm{cos}\left(\mathrm{2x}\right)} \:+\mathrm{2sin}\left(\mathrm{2x}\right)\mathrm{k}\:\mathrm{e}^{\mathrm{cos}\left(\mathrm{2x}\right)} \\ $$$$=\mathrm{2}\:\mathrm{e}^{\mathrm{cos}\left(\mathrm{2x}\right)\:} \:\Rightarrow\:\mathrm{k}^{'} \:\mathrm{e}^{\mathrm{cos}\left(\mathrm{2x}\right)} \:=\mathrm{2e}^{\mathrm{cos}\left(\mathrm{2x}\right)} \:\Rightarrow \\ $$$$\mathrm{k}^{'\:} =\mathrm{2}\:\Rightarrow\mathrm{k}\:=\mathrm{2x}\:+\lambda\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\left(\mathrm{2x}+\lambda\right)\mathrm{e}^{\mathrm{cos}\left(\mathrm{2x}\right)} \\ $$$$\mathrm{y}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow\lambda\:=\mathrm{0}\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{2x}\:\mathrm{e}^{\mathrm{cos}\left(\mathrm{2x}\right)} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com