Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 96479 by  M±th+et+s last updated on 01/Jun/20

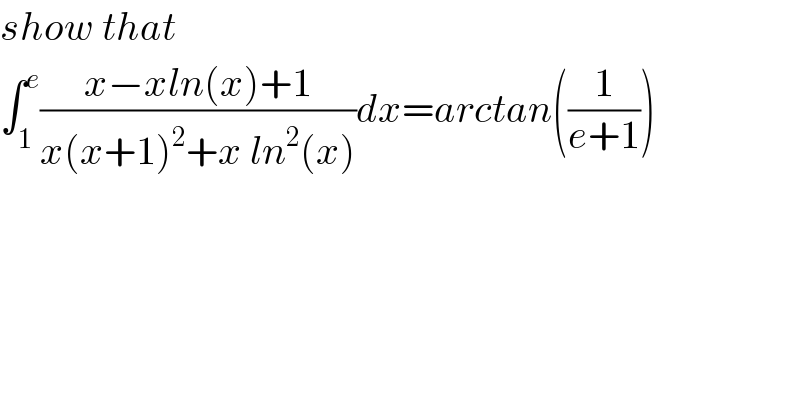
show that ∫_1 ^e ((x−xln(x)+1)/(x(x+1)^2 +x ln^2 (x)))dx=arctan((1/(e+1)))

showthat∫1ex−xln(x)+1x(x+1)2+xln2(x)dx=arctan(1e+1)

Answered by Sourav mridha last updated on 01/Jun/20

let ln(x)=u,then ∫_0 ^1 (((e^u −ue^u +1))/((e^u +1)^2 +u^2 ))du =−∫_0 ^1 ((d(((e^u +1)/u)))/((((e^u +1)/u))^2 +1^2 ))=−[tan^(−1) ((((e^u +1)/u)/1))]_0 ^1 =−tan^(−1) (e+1)+(𝛑/2)=tan^(−1) [(1/(e+1))]

letln(x)=u,then∫01(eu−ueu+1)(eu+1)2+u2du=−∫01d(eu+1u)(eu+1u)2+12=−[tan−1(eu+1u1)]01=−tan−1(e+1)+π2=tan−1[1e+1]

Commented by  M±th+et+s last updated on 01/Jun/20

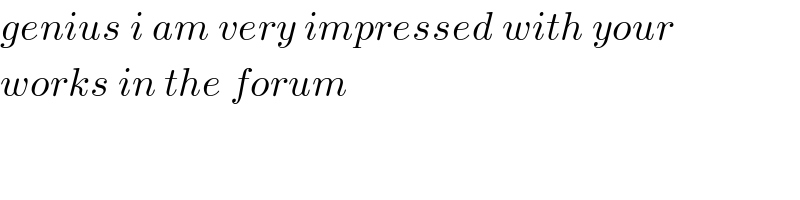
genius i am very impressed with your works in the forum

geniusiamveryimpressedwithyourworksintheforum

Commented by Sourav mridha last updated on 01/Jun/20

thank you very much

Terms of Service

Privacy Policy

Contact: info@tinkutara.com