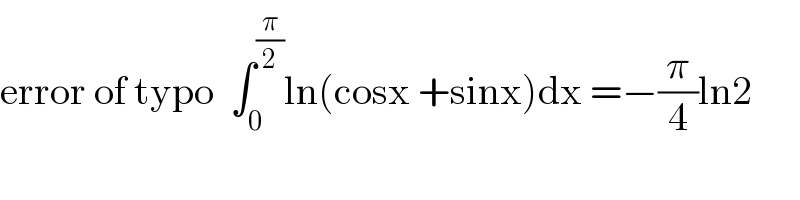calculateI = ∫_0 ^(π/2) ln(cosx +sinx)dx and J =∫


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 96495 by abdomathmax last updated on 01/Jun/20

$calculateI = \int_{0}^{\frac{π}{2}} \ln (cosx + sinx) dx$ $and J = \int_{0}^{\frac{π}{2}} \ln (cosx - sinx) dx$
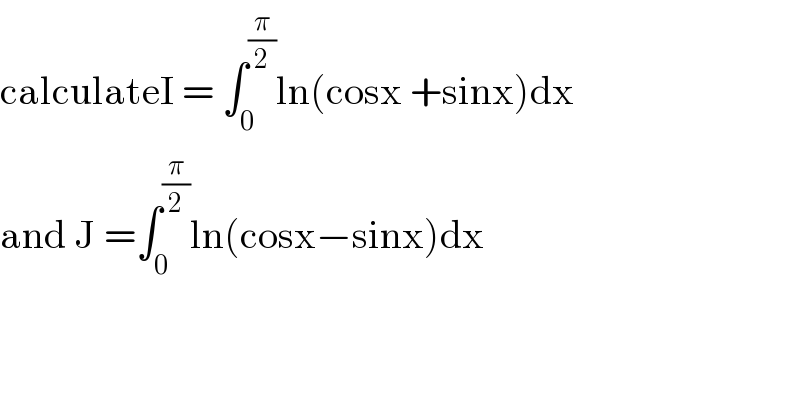
	Answered by Sourav mridha last updated on 02/Jun/20

	$J - I = \int_{0}^{\frac{π}{2}} l n [t a n (\frac{π}{4} - x)] d x . . . (i)$ $a n d a l s o J - I = \int_{0}^{\frac{π}{2}} l n [c o t (\frac{π}{4} - x)] d x$ $. . . . . . . . . (i i)$ $(i) + (i i) w e g e t . . J - I = 0, J = I . . . . (g)$ $n o w J + I = \int_{0}^{\frac{π}{2}} l n (c o s 2 x) d x . . . (v)$ $n o w 2 x = t, t h e n$ $2 J = \frac{1}{2} \int_{0}^{π} l n (c o s t) d t w e c a n a l s o$ $w r i t e t h i s a s - -$ $2 J = \int_{0}^{\frac{π}{2}} l n (c o s t) d t . . . . (a)$ $s o, 2 J = \int_{0}^{\frac{π}{2}} l n (s i n t) d t . . . . (b)$ $(a) + (b) 4 J = \frac{π}{2} l n (\frac{1}{2}) + \int_{0}^{\frac{π}{2}} l n (s i n (2 t)) d t$ $b y a p p l y : the s a m e a p p r o c h l i k e$ ${e q}^{n} (v) w e g e t, \int_{0}^{\frac{π}{2}} l n (s i n 2 t) d t = 2 J$ $so, 4 J = \frac{π}{2} l n (\frac{1}{2}) + 2 J$ $so, 2 J = \frac{π}{2} \ln (\frac{1}{2})$ $now f r o m (g) I = J = \frac{π}{4} l n (\frac{1}{2})$
	Commented by abdomathmax last updated on 02/Jun/20

	$thanks sir .$
	Commented by Sourav mridha last updated on 02/Jun/20
	welcome....
	Answered by mathmax by abdo last updated on 02/Jun/20

	$let f (a) = \int_{0}^{\frac{π}{2}} \ln (cosx + asinx) dx we have f^{^{'}} (a) = \int_{0}^{\frac{π}{2}} \frac{sinx}{cosx + asinx} dx$ $= \int_{0}^{\frac{π}{2}} \frac{dx}{a + \frac{1}{tanx}} =_{tanx = u} \int_{0}^{\infty} \frac{du}{(1 + u^{2}) (a + \frac{1}{u})} = \int_{0}^{\infty} \frac{udu}{(au + 1) (u^{2} + 1)}$ $let decompose F (u) = \frac{u}{(au + 1) (u^{2} + 1)} \Rightarrow F (u) = \frac{α}{au + 1} + \frac{β u + λ}{u^{2} + 1}$ $α = \frac{- 1}{a (\frac{1}{a^{2}} + 1)} = \frac{- a^{2}}{a (1 + a^{2})} = \frac{- a}{1 + a^{2}}$ $\lim_{u \to + \infty} uF (u) = 0 = \frac{α}{a} + β \Rightarrow β = - \frac{α}{a} = \frac{1}{1 + a^{2}}$ $F (0) = 0 = α + λ \Rightarrow λ = \frac{a}{1 + a^{2}} \Rightarrow F (u) = - \frac{a}{(1 + a^{2}) (au + 1)} + \frac{1}{1 + a^{2}} \times \frac{u + a}{u^{2} + 1}$ $\Rightarrow \int_{0}^{\infty} F (u) du = - \frac{a}{1 + a^{2}} \int_{0}^{\infty} \frac{du}{au + 1} + \frac{1}{2 (1 + a^{2})} \int_{0}^{\infty} \frac{2 u}{u^{2} + 1} + \frac{a}{1 + a^{2}} \int_{0}^{\infty} \frac{du}{u^{2} + 1}$ $= \frac{1}{1 + a^{2}} {[\ln \sqrt{u^{2} + 1} - \ln (au + 1)]}_{0}^{\infty} + \frac{π a}{2 (1 + a^{2})}$ $= \frac{1}{1 + a^{2}} {[\ln (\frac{\sqrt{1 + u^{2}}}{au + 1})]}_{0}^{\infty} + \frac{π a}{2 (1 + a^{2})} = - \frac{\ln (a)}{1 + a^{2}} + \frac{π a}{2 (1 + a^{2})} \Rightarrow$ $f (a) = - \int_{0}^{a} \frac{lnt}{1 + t^{2}} dt + \frac{π}{4} \ln (1 + a^{2}) + c but$ $f (0) = c = - \frac{π}{2} \ln (2) \Rightarrow f (a) = \frac{π}{4} \ln (1 + a^{2}) - \frac{π}{2} \ln (2) - \int_{0}^{a} \frac{lnt}{1 + t^{2}} dt$ $\int_{0}^{\frac{π}{2}} \ln (cosx + sinx) dx = f (1) = \frac{π}{4} \ln (2) - \frac{π}{2} \ln (2) - \int_{0}^{1} \frac{lnt}{1 + t^{2}} dt (\to t = \tan θ)$ $= - \frac{π}{4} \ln (2) - \int_{0}^{\frac{π}{2}} \ln (\tan θ) d θ = - \frac{π}{4} \ln (2) - 0 (because \int_{0}^{\frac{π}{2}} \ln (\cos θ) d θ = \int_{0}^{\frac{π}{2}} \ln (\sin θ) d θ) \Rightarrow$ $\Rightarrow \int_{0}^{\frac{π}{2}} \ln (cosx - sinx) dx = - \frac{π}{4} \ln (2)$
	Commented by mathmax by abdo last updated on 02/Jun/20

	$error of typo \int_{0}^{\frac{π}{2}} \ln (cosx + sinx) dx = - \frac{π}{4} \ln 2$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum