solve y^(′′) −2y^′ +y =(x+1)^2 e^(−x) with y(0)=−1 ,y^′ (0)=0 ,y^((2)) (0) =1


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 96571 by mathmax by abdo last updated on 02/Jun/20

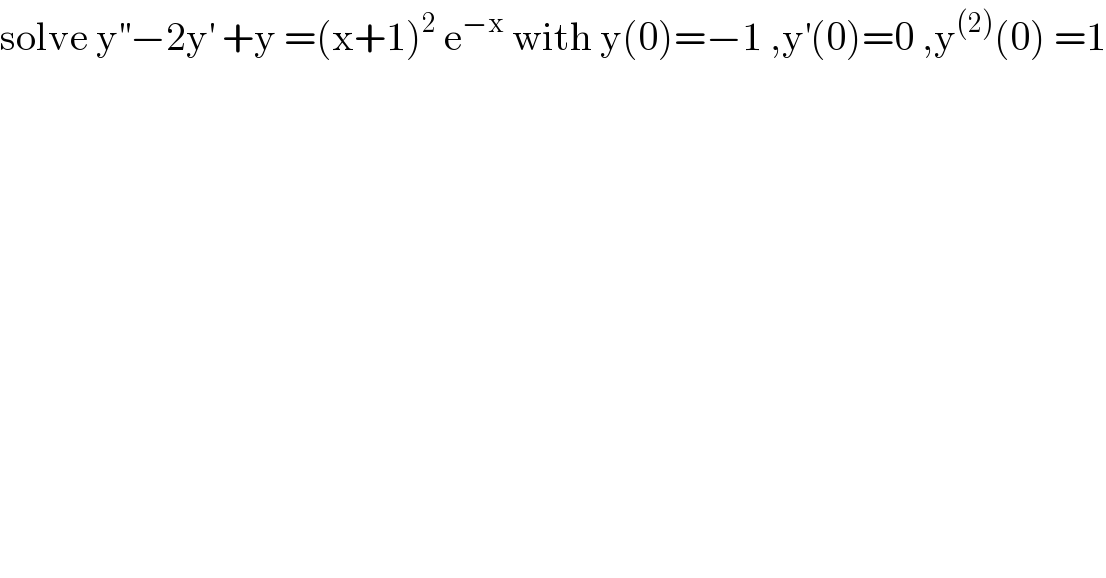
$solve y^{^{″}} - {2 y}^{^{'}} + y = {(x + 1)}^{2} e^{- x} with y (0) = - 1, y^{^{'}} (0) = 0, y^{(2)} (0) = 1$
	Answered by mathmax by abdo last updated on 03/Jun/20
	$let solve by laplace transform (e)⇒L(y^(′′) )−2L(y^′ )+L(y) =L((x+1)^2 e^(−x) ) ⇒ x^2 L(y)−x y(0)−y^′ (0)−2(xL(y)−y(o))+L(y) =L{(x+1)^2 e^(−x) } ⇒ (x^2 −2x+1)L(y)+x−2 =L{(x+1)^2 e^(−x) } ⇒ (x^2 −2x+1)L(y)=−x+2 +L{(x+1)^2 e^(−x) } L{(x+1)^2 e^(−x) } =∫_0 ^∞ (t+1)^2 e^(−t) e^(−xt) dt =∫_0 ^∞ (t+1)^2 e^(−(x+1)t) dt =_(by parts) [(((t+1)^2 )/(−(x+1))) e^(−(x+1)t) ]_0 ^∞ −∫_0 ^∞ 2(t+1)×(1/(−(x+1)))e^(−(x+1)t) dt =(1/(x+1)) +(2/(x+1))∫_0 ^∞ (t+1)e^(−(x+1)t) [dt =(1/(x+1)) +(2/(x+1)){ [((t+1)/(−(x+1)))e^(−(x+1)t) ]_0 ^∞ −∫_0 ^∞ (1/(−(x+1)))e^(−(x+1)t) dt} =(1/(x+1)) +(2/(x+1)){ (1/(x+1)) +(1/(x+1))[(1/(−(x+1)))e^(−(x+1)t) ]_0 ^∞ } =(1/(x+1)) +(2/((x+1)^2 )){ 1+(1/(x+1))} =(1/(x+1)) +(2/((x+1)^2 )) +(2/((x+1)^3 )) (e)⇒(x^2 −2x+1)L(y) =−x+2 +(1/(x+1)) +(2/((x+1)^2 )) +(2/((x+1)^3 )) ⇒ L(y) =((−x+2)/(x^2 −2x+1)) +(1/((x+1)(x^2 −2x+1))) +(2/((x+1)^2 (x^2 −2x+1))) +(2/((x+1)^3 (x^2 −2x+1))) =((−x+2)/((x−1)^2 )) +(1/((x+1)(x−1)^2 )) +(2/((x+1)^2 (x−1)^2 )) +(2/((x+1)^3 (x−1)^2 )) ⇒ y =L^(−1) (((−x+2)/((x−1)^2 )))+L^(−1) ((1/((x+1)(x−1)^2 )))+L^(−1) ((2/((x+1)^( (x−1)^2 ))) +L^(−1) ((2/((x+1)^3 (x−1)^2 ))) ...be continued...$
	$let solve by laplace transform$ $(e) \Rightarrow L (y^{^{″}}) - 2 L (y^{^{'}}) + L (y) = L ({(x + 1)}^{2} e^{- x}) \Rightarrow$ $x^{2} L (y) - x y (0) - y^{^{'}} (0) - 2 (xL (y) - y (o)) + L (y) = L {{(x + 1)}^{2} e^{- x}} \Rightarrow$ $(x^{2} - 2 x + 1) L (y) + x - 2 = L {{(x + 1)}^{2} e^{- x}} \Rightarrow$ $(x^{2} - 2 x + 1) L (y) = - x + 2 + L {{(x + 1)}^{2} e^{- x}}$ $L {{(x + 1)}^{2} e^{- x}} = \int_{0}^{\infty} {(t + 1)}^{2} e^{- t} e^{- xt} dt = \int_{0}^{\infty} {(t + 1)}^{2} e^{- (x + 1) t} dt$ $=_{by parts} {[\frac{{(t + 1)}^{2}}{- (x + 1)} e^{- (x + 1) t}]}_{0}^{\infty} - \int_{0}^{\infty} 2 (t + 1) \times \frac{1}{- (x + 1)} e^{- (x + 1) t} dt$ $= \frac{1}{x + 1} + \frac{2}{x + 1} \int_{0}^{\infty} (t + 1) e^{- (x + 1) t} [dt$ $= \frac{1}{x + 1} + \frac{2}{x + 1} {{[\frac{t + 1}{- (x + 1)} e^{- (x + 1) t}]}_{0}^{\infty} - \int_{0}^{\infty} \frac{1}{- (x + 1)} e^{- (x + 1) t} dt}$ $= \frac{1}{x + 1} + \frac{2}{x + 1} {\frac{1}{x + 1} + \frac{1}{x + 1} {[\frac{1}{- (x + 1)} e^{- (x + 1) t}]}_{0}^{\infty}}$ $= \frac{1}{x + 1} + \frac{2}{{(x + 1)}^{2}} {1 + \frac{1}{x + 1}} = \frac{1}{x + 1} + \frac{2}{{(x + 1)}^{2}} + \frac{2}{{(x + 1)}^{3}}$ $(e) \Rightarrow (x^{2} - 2 x + 1) L (y) = - x + 2 + \frac{1}{x + 1} + \frac{2}{{(x + 1)}^{2}} + \frac{2}{{(x + 1)}^{3}} \Rightarrow$ $L (y) = \frac{- x + 2}{x^{2} - 2 x + 1} + \frac{1}{(x + 1) (x^{2} - 2 x + 1)} + \frac{2}{{(x + 1)}^{2} (x^{2} - 2 x + 1)} + \frac{2}{{(x + 1)}^{3} (x^{2} - 2 x + 1)}$ $= \frac{- x + 2}{{(x - 1)}^{2}} + \frac{1}{(x + 1) {(x - 1)}^{2}} + \frac{2}{{(x + 1)}^{2} {(x - 1)}^{2}} + \frac{2}{{(x + 1)}^{3} {(x - 1)}^{2}} \Rightarrow$ $y = L^{- 1} (\frac{- x + 2}{{(x - 1)}^{2}}) + L^{- 1} (\frac{1}{(x + 1) {(x - 1)}^{2}}) + L^{- 1} (\frac{2}{{(x + 1)}^{(} {(x - 1)}^{2}}) + L^{- 1} (\frac{2}{{(x + 1)}^{3} {(x - 1)}^{2}})$ $. . . be continued . . .$
	Answered by mathmax by abdo last updated on 03/Jun/20

	$wronkien method (he) \to y^{(2)} - {2 y}^{(1)} + y = 0 \to r^{2} - 2 r + 1 = 0 \Rightarrow {(r - 1)}^{2} = 0 \Rightarrow$ $r = 1 \Rightarrow y_{h} = (ax + b) e^{x} = {axe}^{x} + {be}^{x} = {au}_{1} + {bu}_{2}, u_{1} = {xe}^{x} and u_{2} = e^{x}$ $W (u_{1}, u_{2}) = \| \begin{matrix} u_{1} u_{2} \\ u_{1}^{^{'}} u_{2}^{^{'}} \end{matrix} \| = \| \begin{matrix} {xe}^{x} e^{x} \\ (x + 1) e^{x} e^{x} \end{matrix} \| = {xe}^{2 x} - (x + 1) e^{2 x} = - e^{2 x}$ $W_{1} = \| \begin{matrix} 0 e^{x} \\ {(x + 1)}^{2} e^{- x} e^{x} \end{matrix} \| = - {(x + 1)}^{2}$ $W_{2} = \| \begin{matrix} {xe}^{x} 0 \\ (x + 1) e^{x} {(x + 1)}^{2} e^{- x} \end{matrix} \| = x {(x + 1)}^{2}$ $v_{1} = \int \frac{w_{1}}{W} dx = \int \frac{- {(x + 1)}^{2}}{- e^{2 x}} dx = \int {(x + 1)}^{2} e^{- 2 x} dx$ $= - \frac{1}{2} {(x + 1)}^{2} e^{- 2 x} - \int 2 (x + 1) \times (- \frac{1}{2}) e^{- 2 x} dx$ $= - \frac{1}{2} {(x + 1)}^{2} e^{- 2 x} + \int (x + 1) e^{- 2 x} dx$ $= - \frac{1}{2} {(x + 1)}^{2} - \frac{x + 1}{2} e^{- 2 x} + \frac{1}{2} \int e^{- 2 x} dx$ $= - \frac{{(x + 1)}^{2}}{2} - \frac{(x + 1) e^{- 2 x}}{2} - \frac{1}{4} e^{- 2 x}$ $v_{2} = \int \frac{w 2}{W} dx = \int \frac{x {(x + 1)}^{2}}{- e^{2 x}} dx = - \int x (x^{2} + 2 x + 1) e^{- 2 x} dx$ $- v_{2} = \int (x^{3} + {2 x}^{2} + x) e^{- 2 x} dx$ $= - \frac{1}{2} (x^{3} + {2 x}^{2} + x) e^{- 2 x} + \frac{1}{2} \int ({3 x}^{2} + 4 x + 1) e^{- 2 x} dx$ $= - \frac{1}{2} (x^{3} + {2 x}^{2} + x) e^{- 2 x} + \frac{1}{2} (- \frac{1}{2} ({3 x}^{2} + 4 x + 1) e^{- 2 x} + \frac{1}{2} \int (6 x + 4) e^{- 2 x} dx)$ $= - \frac{1}{2} (x^{3} + {2 x}^{2} + x) e^{- 2 x} - \frac{1}{4} ({3 x}^{2} + 4 x + 1) e^{- 2 x} + \frac{1}{2} \int (3 x + 2) e^{- 2 x} dx but$ $\int (3 x + 2) e^{- 2 x} dx = - \frac{1}{2} (3 x + 2) e^{- 2 x} + \frac{3}{2} \int e^{- 2 x} dx$ $= - \frac{1}{2} (3 x + 2) e^{- 2 x} - \frac{3}{4} e^{- 2 x} \Rightarrow$ $v_{2} = (\frac{1}{2} (x^{3} + {2 x}^{2} + x) + \frac{1}{4} ({3 x}^{2} + 4 x + 1) + \frac{1}{2} (3 x + 2) + \frac{3}{4}) e^{- 2 x} = . . . .$ $y_{p} = u_{1} v_{1} + u_{2} v_{2} and general solution is$ $y = y_{h} + y_{p} . . . be continued . . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum