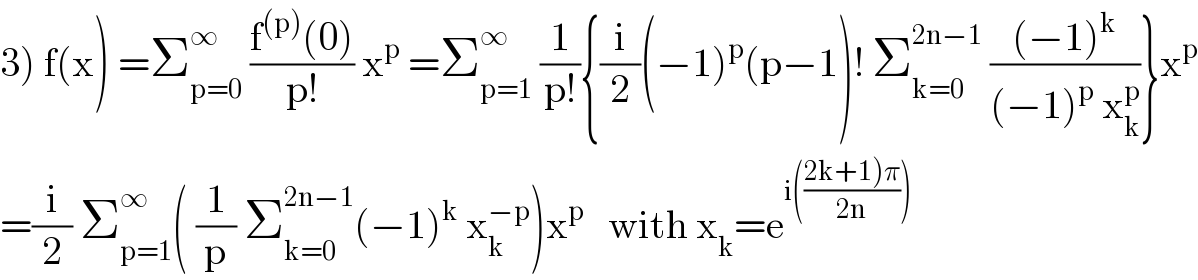let f(x) =arctan(x^n ) with n integr natural 1) calculate f^′ (x) and f^((2)) (x) 2) calculate f^((n)) (x) and f^((n)) (0) 3)developp f at integr serie


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 96593 by mathmax by abdo last updated on 03/Jun/20

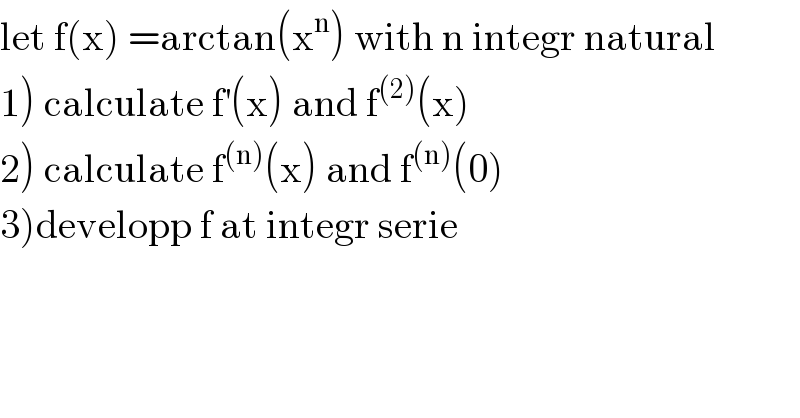
$let f (x) = \arctan (x^{n}) with n integr natural$ $1) calculate f^{^{'}} (x) and f^{(2)} (x)$ $2) calculate f^{(n)} (x) and f^{(n)} (0)$ $3) developp f at integr serie$
	Answered by mathmax by abdo last updated on 03/Jun/20

	$1) we have f (x) = \arctan (x^{n}) \Rightarrow f^{^{'}} (x) = \frac{{nx}^{n - 1}}{1 + x^{2 n}}$ $f^{^{″}} (x) = \frac{n (n - 1) x^{n - 2} (1 + x^{2 n}) - 2 n x^{2 n - 1} . {nx}^{n - 1}}{{(1 + x^{2 n})}^{2}}$ $= \frac{n (n - 1) x^{n - 2} + n (n - 1) x^{3 n - 2} - {2 n}^{2} x^{3 n - 2}}{{(1 + x^{2 n})}^{2}}$ $= \frac{n (n - 1) x^{n - 2} + (n^{2} - n - {2 n}^{2}) x^{3 n - 2}}{{(1 + x^{2 n})}^{2}} = \frac{n (n - 1) x^{n - 2} - (n + n^{2}) x^{3 n - 2}}{{(1 + x^{2 n})}^{2}}$
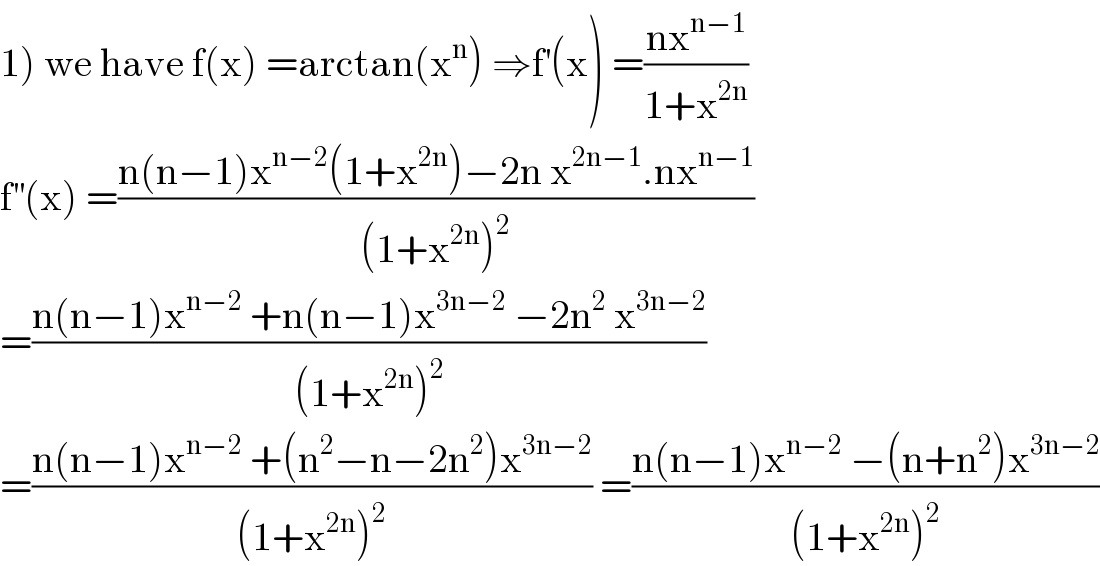
	Answered by mathmax by abdo last updated on 03/Jun/20
	$2)we have f^′ (x) =((nx^(n−1) )/(1+x^(2n) )) poles of f^(′?) x^(2n) +1 =0 ⇒x^(2n) =e^(i(2k+1)π) ⇒x_k =e^(i(((2k+1)π)/(2n))) k∈[[0,2n−1]] ⇒f^′ (x) =((nx^(n−1) )/(Π_(k=0) ^(2n−1) (x−x_k ))) =Σ_(k=0) ^(2n−1) (a_k /(x−x_k )) , a_k =((nx_k ^(n−1) )/(2n x_k ^(2n−1) )) =(1/2)×(x_k ^n /((−1))) =−(1/2) e^(i(((2k+1)π)/2)) ⇒f^′ (x) =−(1/2) Σ_(k=0) ^(2n−1) (e^(i(((2k+1)π)/2))) /(x−x_k )) ⇒ f^((p)) (x) =−(1/2) Σ_(k=0) ^(2n−1) e^(i(πk +(π/2))) {(1/(x−x_k ))}^((p−1)) =−(1/2)Σ_(k=0) ^(2n−1) i(−1)^k ×(((−1)^(p−1) (p−1)!)/((x−x_k )^p )) =((i(−1)^p (p−1)!)/2) Σ_(k=0) ^(2n−1) (((−1)^k )/((x−x_k )^p )) p=n ⇒f^((n)) (x) =(i/2)(−1)^n (n−1)!Σ_(k=0) ^(2n−1) (((−1)^k )/((x−x_k )^n )) f^((n)) (0) =(i/2)(−1)^n (n−1)! Σ_(k=0) ^(2n−1) (((−1)^k )/((−1)^n x_k ^n )) =(i/2)(n−1)! Σ_(k=0) ^(2n−1) (((−1)^k )/(i(−1)^k )) =(1/2) Σ_(k=0) ^(2n−1) (1) =n ⇒f^((n)) (0) =n$
	$2) we have f^{^{'}} (x) = \frac{{nx}^{n - 1}}{1 + x^{2 n}} poles of f^{^{'} ?}$ $x^{2 n} + 1 = 0 \Rightarrow x^{2 n} = e^{i (2 k + 1) π} \Rightarrow x_{k} = e^{i \frac{(2 k + 1) π}{2 n}} k \in [[0, 2 n - 1]]$ $\Rightarrow f^{^{'}} (x) = \frac{{nx}^{n - 1}}{\prod_{k = 0}^{2 n - 1} (x - x_{k})} = \sum_{k = 0}^{2 n - 1} \frac{a_{k}}{x - x_{k}}, a_{k} = \frac{{nx}_{k}^{n - 1}}{2 n x_{k}^{2 n - 1}} = \frac{1}{2} \times \frac{x_{k}^{n}}{(- 1)}$ $= - \frac{1}{2} e^{i \frac{(2 k + 1) π}{2}} \Rightarrow f^{^{'}} (x) = - \frac{1}{2} \sum_{k = 0}^{2 n - 1} \frac{e^{i (\frac{2 k + 1) π}{2})}}{x - x_{k}} \Rightarrow$ $f^{(p)} (x) = - \frac{1}{2} \sum_{k = 0}^{2 n - 1} e^{i (π k + \frac{π}{2})} {\frac{1}{x - x_{k}}}^{(p - 1)}$ $= - \frac{1}{2} \sum_{k = 0}^{2 n - 1} i {(- 1)}^{k} \times \frac{{(- 1)}^{p - 1} (p - 1)!}{{(x - x_{k})}^{p}}$ $= \frac{i {(- 1)}^{p} (p - 1)!}{2} \sum_{k = 0}^{2 n - 1} \frac{{(- 1)}^{k}}{{(x - x_{k})}^{p}}$ $p = n \Rightarrow f^{(n)} (x) = \frac{i}{2} {(- 1)}^{n} (n - 1)! \sum_{k = 0}^{2 n - 1} \frac{{(- 1)}^{k}}{{(x - x_{k})}^{n}}$ $f^{(n)} (0) = \frac{i}{2} {(- 1)}^{n} (n - 1)! \sum_{k = 0}^{2 n - 1} \frac{{(- 1)}^{k}}{{(- 1)}^{n} x_{k}^{n}}$ $= \frac{i}{2} (n - 1)! \sum_{k = 0}^{2 n - 1} \frac{{(- 1)}^{k}}{i {(- 1)}^{k}} = \frac{1}{2} \sum_{k = 0}^{2 n - 1} (1) = n \Rightarrow f^{(n)} (0) = n$
	Commented by mathmax by abdo last updated on 03/Jun/20
	$3) f(x) =Σ_(p=0) ^∞ ((f^((p)) (0))/(p!)) x^p =Σ_(p=1) ^∞ (1/(p!)){(i/2)(−1)^p (p−1)! Σ_(k=0) ^(2n−1) (((−1)^k )/((−1)^p x_k ^p ))}x^p =(i/2) Σ_(p=1) ^∞ ( (1/p) Σ_(k=0) ^(2n−1) (−1)^k x_k ^(−p) )x^p with x_k =e^(i(((2k+1)π)/(2n))))$
	$3) f (x) = \sum_{p = 0}^{\infty} \frac{f^{(p)} (0)}{p!} x^{p} = \sum_{p = 1}^{\infty} \frac{1}{p!} {\frac{i}{2} {(- 1)}^{p} (p - 1)! \sum_{k = 0}^{2 n - 1} \frac{{(- 1)}^{k}}{{(- 1)}^{p} x_{k}^{p}}} x^{p}$ $= \frac{i}{2} \sum_{p = 1}^{\infty} (\frac{1}{p} \sum_{k = 0}^{2 n - 1} {(- 1)}^{k} x_{k}^{- p}) x^{p} with x_{k} = e^{i (\frac{2 k + 1) π}{2 n})}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum