
Question and Answers Forum
Question Number 96602 by Ar Brandon last updated on 03/Jun/20
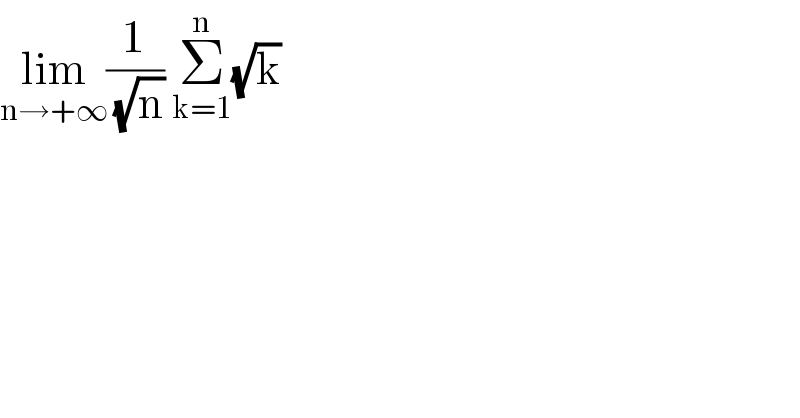
Answered by Sourav mridha last updated on 03/Jun/20
![by inspection Σ_(k=1) ^n (√(k )) this is a diverging series as n⇒∞. proof: using Eular−Maclaurin integration formula.... Σ_(k=1) ^n (√k) =[((16n^2 +12n−5(√n) +1)/(24(√n)))] approximate result..but okkk.. now,lim_(n→∞) (1/(√n))Σ_(k=1) ^n (√k) =lim_(n→∞) [((16n+12−(5/(√n))+(1/n))/(24))] =∞..](Q96611.png)
Answered by mathmax by abdo last updated on 03/Jun/20
![S_n =(1/(√n))Σ_(k=1) ^n (√k) ⇒S_n =Σ_(k=1) ^n (√(k/n))=n×(1/n)Σ_(k=1) ^n (√(k/n)) but lim_(n→+∞) (1/n)(√(k/n))=∫_0 ^1 (√x)dx =∫_0 ^1 x^(1/2) dx =[(2/3)x^(3/2) ]_0 ^1 =(2/3) ⇒ lim_(n→+∞) S_n =lim_(n→+∞) ((2n)/3) =+∞](Q96633.png)
Answered by maths mind last updated on 03/Jun/20
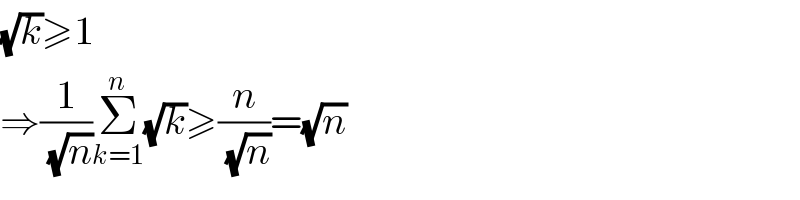
| ||
Question and Answers Forum | ||
Question Number 96602 by Ar Brandon last updated on 03/Jun/20 | ||
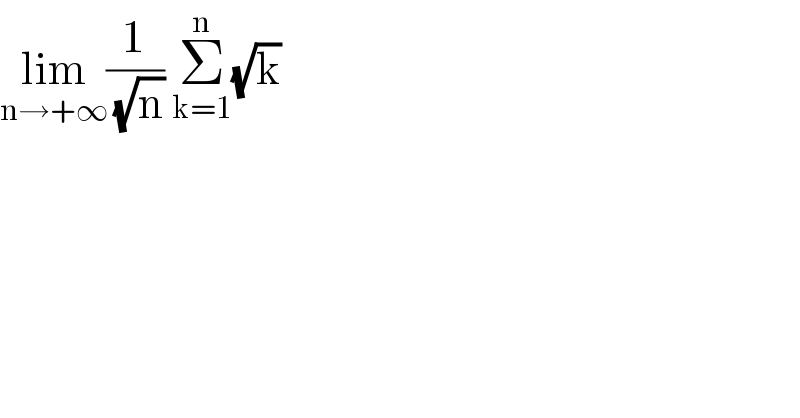 | ||
Answered by Sourav mridha last updated on 03/Jun/20 | ||
![by inspection Σ_(k=1) ^n (√(k )) this is a diverging series as n⇒∞. proof: using Eular−Maclaurin integration formula.... Σ_(k=1) ^n (√k) =[((16n^2 +12n−5(√n) +1)/(24(√n)))] approximate result..but okkk.. now,lim_(n→∞) (1/(√n))Σ_(k=1) ^n (√k) =lim_(n→∞) [((16n+12−(5/(√n))+(1/n))/(24))] =∞..](Q96611.png) | ||
| ||
Answered by mathmax by abdo last updated on 03/Jun/20 | ||
![S_n =(1/(√n))Σ_(k=1) ^n (√k) ⇒S_n =Σ_(k=1) ^n (√(k/n))=n×(1/n)Σ_(k=1) ^n (√(k/n)) but lim_(n→+∞) (1/n)(√(k/n))=∫_0 ^1 (√x)dx =∫_0 ^1 x^(1/2) dx =[(2/3)x^(3/2) ]_0 ^1 =(2/3) ⇒ lim_(n→+∞) S_n =lim_(n→+∞) ((2n)/3) =+∞](Q96633.png) | ||
| ||
Answered by maths mind last updated on 03/Jun/20 | ||
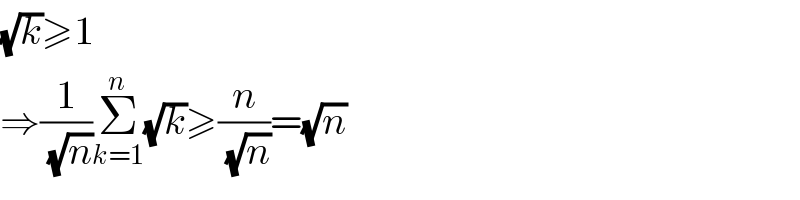 | ||
| ||