Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 96607 by bemath last updated on 03/Jun/20

It is given that f(x) is a function defined on R, satisfying f(1)=1 and for any x∈R, f(x+5) ≥f(x)+5 and f(x+1) ≤f(x)+1. If g(x)= f(x)+1−x, then g(2002) = ___

$$\mathrm{It}\:\mathrm{is}\:\mathrm{given}\:\mathrm{that}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{function} \\ $$$$\mathrm{defined}\:\mathrm{on}\:\mathbb{R},\:\mathrm{satisfying}\:\mathrm{f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{and}\:\mathrm{for}\:\mathrm{any}\:\mathrm{x}\in\mathbb{R},\:\mathrm{f}\left(\mathrm{x}+\mathrm{5}\right)\:\geqslant\mathrm{f}\left(\mathrm{x}\right)+\mathrm{5} \\ $$$$\mathrm{and}\:\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)\:\leqslant\mathrm{f}\left(\mathrm{x}\right)+\mathrm{1}.\:\mathrm{If}\:\mathrm{g}\left(\mathrm{x}\right)= \\ $$$$\mathrm{f}\left(\mathrm{x}\right)+\mathrm{1}−\mathrm{x},\:\mathrm{then}\:\mathrm{g}\left(\mathrm{2002}\right)\:=\:\_\_\_ \\ $$

Commented by bobhans last updated on 03/Jun/20

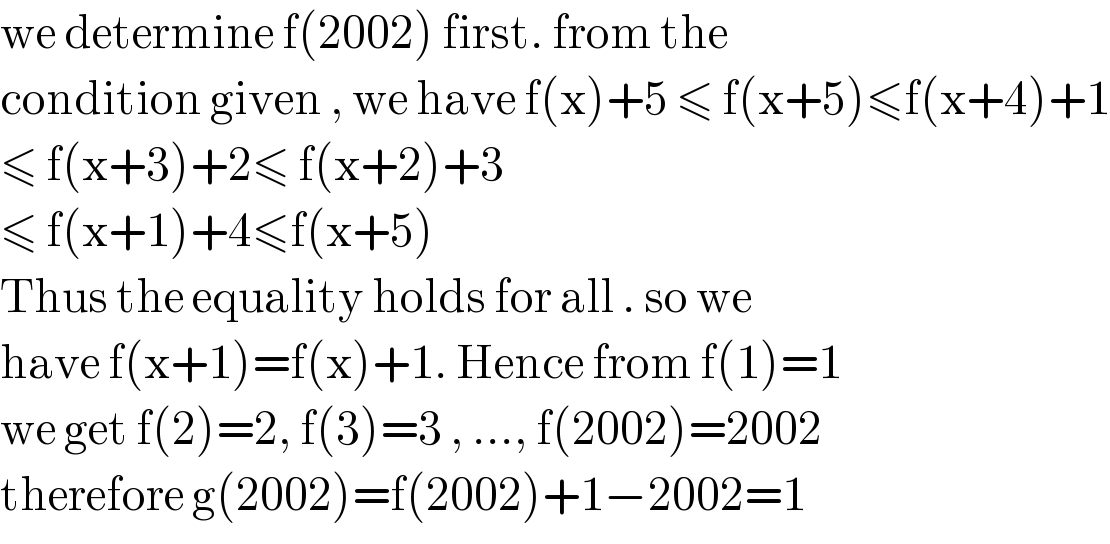
we determine f(2002) first. from the condition given , we have f(x)+5 ≤ f(x+5)≤f(x+4)+1 ≤ f(x+3)+2≤ f(x+2)+3 ≤ f(x+1)+4≤f(x+5) Thus the equality holds for all . so we have f(x+1)=f(x)+1. Hence from f(1)=1 we get f(2)=2, f(3)=3 , ..., f(2002)=2002 therefore g(2002)=f(2002)+1−2002=1

$$\mathrm{we}\:\mathrm{determine}\:\mathrm{f}\left(\mathrm{2002}\right)\:\mathrm{first}.\:\mathrm{from}\:\mathrm{the} \\ $$$$\mathrm{condition}\:\mathrm{given}\:,\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{x}\right)+\mathrm{5}\:\leqslant\:\mathrm{f}\left(\mathrm{x}+\mathrm{5}\right)\leqslant\mathrm{f}\left(\mathrm{x}+\mathrm{4}\right)+\mathrm{1} \\ $$$$\leqslant\:\mathrm{f}\left(\mathrm{x}+\mathrm{3}\right)+\mathrm{2}\leqslant\:\mathrm{f}\left(\mathrm{x}+\mathrm{2}\right)+\mathrm{3} \\ $$$$\leqslant\:\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{4}\leqslant\mathrm{f}\left(\mathrm{x}+\mathrm{5}\right) \\ $$$$\mathrm{Thus}\:\mathrm{the}\:\mathrm{equality}\:\mathrm{holds}\:\mathrm{for}\:\mathrm{all}\:.\:\mathrm{so}\:\mathrm{we}\: \\ $$$$\mathrm{have}\:\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)=\mathrm{f}\left(\mathrm{x}\right)+\mathrm{1}.\:\mathrm{Hence}\:\mathrm{from}\:\mathrm{f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{f}\left(\mathrm{2}\right)=\mathrm{2},\:\mathrm{f}\left(\mathrm{3}\right)=\mathrm{3}\:,\:...,\:\mathrm{f}\left(\mathrm{2002}\right)=\mathrm{2002} \\ $$$$\mathrm{therefore}\:\mathrm{g}\left(\mathrm{2002}\right)=\mathrm{f}\left(\mathrm{2002}\right)+\mathrm{1}−\mathrm{2002}=\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com