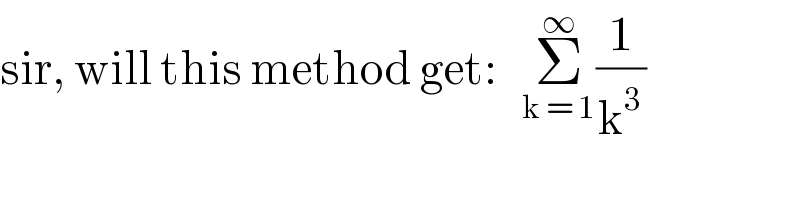Question Number 96667 by Ar Brandon last updated on 03/Jun/20
$$\mathcal{P}\mathrm{rove}\:\:\mathrm{that}\:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$
Answered by Sourav mridha last updated on 03/Jun/20
$$\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\boldsymbol{{k}}^{−\mathrm{2}} =\boldsymbol{\zeta}\left(\mathrm{2}\right) \\ $$$$\boldsymbol{{f}}\mathrm{ro}\boldsymbol{{m}}\:\boldsymbol{{the}}\:\boldsymbol{{relation}}\:\boldsymbol{{of}}\:\boldsymbol{{Ri}}\mathrm{e}\boldsymbol{{mann}} \\ $$$$\boldsymbol{{zeta}}\:\boldsymbol{{f}}^{\boldsymbol{{n}}} \:\boldsymbol{{with}}\:\boldsymbol{{Burnoulli}}\:\boldsymbol{{number}} \\ $$$$\left(\boldsymbol{{even}}\right). \\ $$$$\:\:\:\:\:\:\:\boldsymbol{{B}}_{\mathrm{2}\boldsymbol{{n}}} =\left(−\mathrm{1}\right)^{\boldsymbol{{n}}−\mathrm{1}} \frac{\mathrm{2}\left(\mathrm{2}\boldsymbol{{n}}\right)!}{\left(\mathrm{2}\boldsymbol{\pi}\right)^{\mathrm{2}\boldsymbol{{n}}} }.\boldsymbol{\zeta}\left(\mathrm{2}\boldsymbol{{n}}\right). \\ $$$$\:\:\:\:\:\boldsymbol{{put}}..\boldsymbol{{n}}=\mathrm{1} \\ $$$$\:\:\:\:\boldsymbol{{then}},\boldsymbol{{B}}_{\mathrm{2}} =\frac{\mathrm{2}.\mathrm{2}!}{\mathrm{2}.\mathrm{2}.\boldsymbol{\pi}^{\mathrm{2}} \:}.\boldsymbol{\zeta}\left(\mathrm{2}\right) \\ $$$$\boldsymbol{{we}}\:\boldsymbol{{know}}\:\boldsymbol{{B}}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{6}}.\boldsymbol{{now}}\:\boldsymbol{{putting}}\:\boldsymbol{{it}} \\ $$$$\boldsymbol{{we}}\:\boldsymbol{{get}}..\boldsymbol{\zeta}\left(\mathrm{2}\right)=\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{6}}... \\ $$
Commented by I want to learn more last updated on 05/Jun/20
$$\mathrm{sir}\:\mathrm{what}\:\mathrm{of}\:\:\:\:\zeta\left(\mathrm{2}\boldsymbol{\mathrm{n}}\:\:+\:\:\mathrm{1}\right)\:\:\:\boldsymbol{\mathrm{for}}\:\:\boldsymbol{\mathrm{odd}} \\ $$
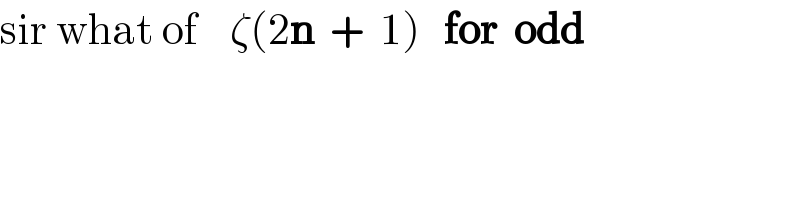
Commented by Sourav mridha last updated on 05/Jun/20
![This is not justified by this formula because: B_(2n+1) =0 where n∈N only odd number B_1 =−(1/2) exist. generel form of B_n : B_n =−((n!)/((2𝛑i)^n ))[Σ_(m=1) ^∞ ((1/m^n )+(1/((−m)^n )))]](Q96916.png)
$$\boldsymbol{{T}}\mathrm{his}\:\boldsymbol{{is}}\:\boldsymbol{{not}}\:\boldsymbol{{justified}}\:\boldsymbol{{by}}\:\boldsymbol{{this}}\: \\ $$$$\boldsymbol{{formula}}\:\boldsymbol{{because}}: \\ $$$$\:\:\:\boldsymbol{{B}}_{\mathrm{2}\boldsymbol{{n}}+\mathrm{1}} =\mathrm{0}\:\boldsymbol{{where}}\:\boldsymbol{{n}}\in\mathbb{N} \\ $$$$\boldsymbol{{only}}\:\boldsymbol{{odd}}\:\boldsymbol{{number}}\:\boldsymbol{{B}}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}\:\boldsymbol{{exist}}. \\ $$$$\:\:\:\:\:\:\boldsymbol{{generel}}\:\boldsymbol{{form}}\:\boldsymbol{{of}}\:\boldsymbol{{B}}_{\boldsymbol{{n}}} : \\ $$$$\:\:\:\:\:\:\:\boldsymbol{{B}}_{\boldsymbol{{n}}} =−\frac{\boldsymbol{{n}}!}{\left(\mathrm{2}\boldsymbol{\pi{i}}\right)^{\boldsymbol{{n}}} }\left[\underset{\mathrm{m}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\boldsymbol{{m}}^{\boldsymbol{{n}}} }+\frac{\mathrm{1}}{\left(−\boldsymbol{{m}}\right)^{\boldsymbol{{n}}} }\right)\right]\: \\ $$$$\:\: \\ $$$$ \\ $$
Commented by I want to learn more last updated on 06/Jun/20
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by Rio Michael last updated on 03/Jun/20
![i′ve always Wanted to Get this proof..and here′s what i fell on. Σ_(k=1) ^∞ (1/k^2 ) = (π^2 /6) first let s = arcsin x hence ∫_0 ^(π/2) s ds = (π^2 /8) also ∫_0 ^1 ((arcsin x)/(√(1−x^2 ))) dx = (π^2 /8) since arc sin x = ∫_0 ^1 (1/((√(1−x^2 )) )) dx = x + (x^3 /(2 ×3)) + ((1 × 3 x^5 )/(2 ×5 ×5)) +... substituting we get: ∫_0 ^1 ((dx/(√(1−x^2 ))) ∫(dx/(√(1−x^2 )))) = ∫_0 ^1 [x + (x^3 /6)((dx/(√(1−x^2 ))))+...] realise that : ∫_0 ^1 (x^(2n+1) /(√(1−x^2 ))) dx = ((2n!!)/((2n + 1)!!)). since we get all odd powers, (π^2 /8) = Σ_(k=1) ^∞ (1/((2n−1)^2 )) if we define x = Σ_(k=1) ^∞ (1/k^2 ) dividing by 4 , we get the equation: x = (π^2 /6) = Σ_(k=1) ^∞ (1/k^2 ) please guys check.](Q96674.png)
$$\mathrm{i}'\mathrm{ve}\:\mathrm{always}\:\mathcal{W}\mathrm{anted}\:\mathrm{to}\:\mathcal{G}\mathrm{et}\:\mathrm{this}\:\mathrm{proof}..\mathrm{and}\:\mathrm{here}'\mathrm{s}\:\mathrm{what}\:\mathrm{i}\:\mathrm{fell}\:\mathrm{on}. \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\mathrm{first}\:\mathrm{let}\:{s}\:=\:\mathrm{arcsin}\:{x}\: \\ $$$$\mathrm{hence}\:\:\overset{\frac{\pi}{\mathrm{2}}} {\int}_{\mathrm{0}} \:{s}\:{ds}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\mathrm{also}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{arcsin}\:{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:{dx}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\mathrm{since}\:\:\mathrm{arc}\:\mathrm{sin}\:{x}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:}\:{dx}\:=\:{x}\:+\:\frac{{x}^{\mathrm{3}} }{\mathrm{2}\:×\mathrm{3}}\:\:+\:\frac{\mathrm{1}\:×\:\mathrm{3}\:{x}^{\mathrm{5}} }{\mathrm{2}\:×\mathrm{5}\:×\mathrm{5}}\:+...\: \\ $$$$\mathrm{substituting}\:\mathrm{we}\:\mathrm{get}:\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{{dx}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\int\frac{{dx}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left[{x}\:+\:\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\left(\frac{{dx}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right)+...\right] \\ $$$$\mathrm{realise}\:\mathrm{that}\::\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:{dx}\:=\:\frac{\mathrm{2}{n}!!}{\left(\mathrm{2}{n}\:+\:\mathrm{1}\right)!!}.\:\mathrm{since}\:\mathrm{we}\:\mathrm{get}\:\mathrm{all}\:\mathrm{odd}\:\mathrm{powers}, \\ $$$$\:\:\:\:\:\:\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{define}\:{x}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} } \\ $$$$\mathrm{dividing}\:\mathrm{by}\:\mathrm{4}\:,\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{equation}:\:{x}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} } \\ $$$$\mathrm{please}\:\mathrm{guys}\:\mathrm{check}. \\ $$
Commented by Ar Brandon last updated on 03/Jun/20
I'm lost.��
Commented by I want to learn more last updated on 06/Jun/20
$$\mathrm{thanks}\:\mathrm{sir} \\ $$
Commented by I want to learn more last updated on 06/Jun/20
$$\mathrm{sir},\:\mathrm{will}\:\mathrm{this}\:\mathrm{method}\:\mathrm{get}:\:\:\:\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{3}} } \\ $$