
Question Number 96684 by Ar Brandon last updated on 03/Jun/20
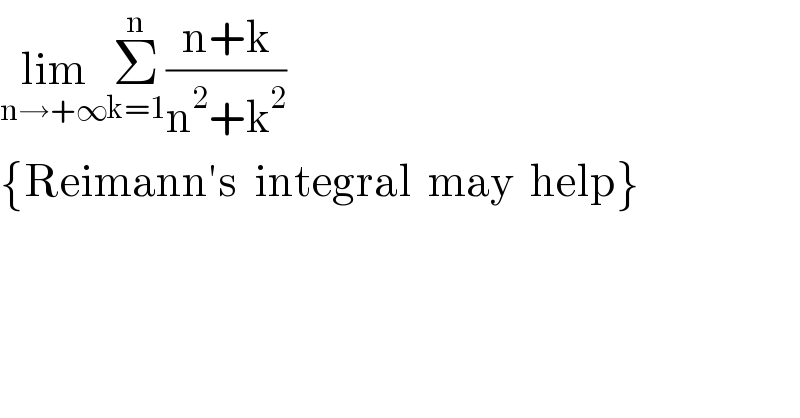
$$\underset{\mathrm{n}\rightarrow+\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{n}+\mathrm{k}}{\mathrm{n}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} } \\ $$$$\left\{\mathrm{Reimann}'\mathrm{s}\:\:\mathrm{integral}\:\:\mathrm{may}\:\:\mathrm{help}\right\} \\ $$
Answered by Sourav mridha last updated on 03/Jun/20
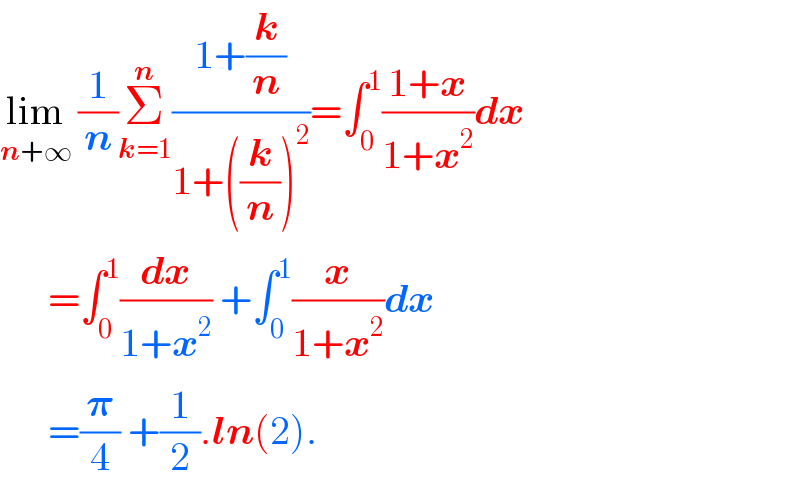
$$\underset{\boldsymbol{{n}}+\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\boldsymbol{{n}}}\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\frac{\mathrm{1}+\frac{\boldsymbol{{k}}}{\boldsymbol{{n}}}}{\mathrm{1}+\left(\frac{\boldsymbol{{k}}}{\boldsymbol{{n}}}\right)^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}+\boldsymbol{{x}}}{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }\boldsymbol{{dx}} \\ $$$$\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{{dx}}}{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }\:+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{{x}}}{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }\boldsymbol{{dx}} \\ $$$$\:\:\:\:\:\:=\frac{\boldsymbol{\pi}}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}.\boldsymbol{{ln}}\left(\mathrm{2}\right). \\ $$
Commented by Ar Brandon last updated on 03/Jun/20
cool, thanks
Answered by mathmax by abdo last updated on 03/Jun/20
![let A_n =Σ_(n=1) ^∞ ((n+k)/(n^2 +k^2 )) ⇒ A_n =(1/n)Σ_(n=1) ^∞ ((1+(k/n))/(1+((k/n))^2 )) so A_n is Rieman sum and lim_(n→+∞) A_n =∫_0 ^1 ((1+x)/(1+x^2 ))dx =∫_0 ^1 (dx/(1+x^2 )) +∫_0 ^1 ((xdx)/(1+x^2 )) =[arctanx]_0 ^1 +[(1/2)ln(1+x^2 )]_0 ^1 =(π/4) +((ln2)/2)](Q96694.png)
$$\mathrm{let}\:\mathrm{A}_{\mathrm{n}} =\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}+\mathrm{k}}{\mathrm{n}^{\mathrm{2}} \:+\mathrm{k}^{\mathrm{2}} }\:\Rightarrow\:\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}}{\mathrm{1}+\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} }\:\mathrm{so}\:\mathrm{A}_{\mathrm{n}} \mathrm{is}\:\mathrm{Rieman}\:\mathrm{sum}\:\mathrm{and} \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}+\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{xdx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\left[\mathrm{arctanx}\right]_{\mathrm{0}} ^{\mathrm{1}} \:+\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{ln2}}{\mathrm{2}} \\ $$
