Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 96746 by MJS last updated on 04/Jun/20

$$\int \frac{\sqrt{x}}{(1+x^3)\sqrt{1-x^3}}dx=?$$$$\int \frac{\sqrt{x}}{(1-x^3)\sqrt{1+x^3}}dx=?$$

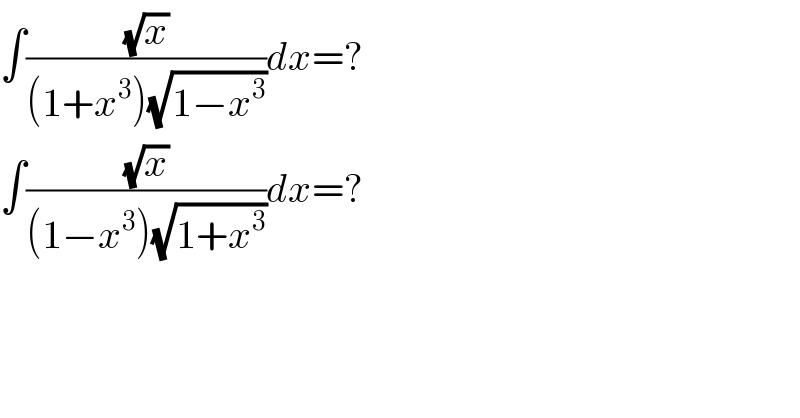
Commented by bemath last updated on 04/Jun/20

I have no idea to solve this integral

Commented by MJS last updated on 05/Jun/20

$$\mathrm{thank}\mathrm{you}\mathrm{everybody}!$$$$\mathrm{how}\mathrm{to}\mathrm{reach}$$$$\int \frac{\sqrt{x}}{(1+x^3)\sqrt{1-x^3}}dx=-\frac{\sqrt{2}}{3}\arcsin \sqrt{\frac{1-x^3}{1+x^3}}?$$

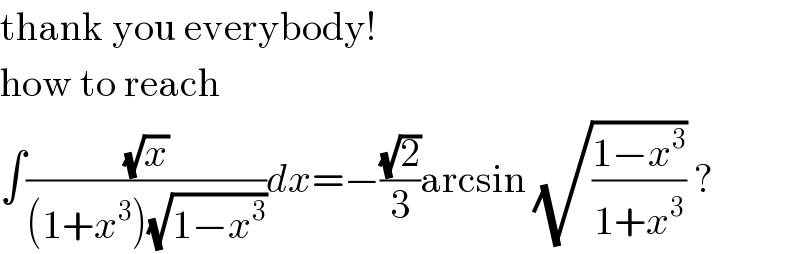
Answered by  M±th+et+s last updated on 04/Jun/20

$$\int \frac{\sqrt{x}}{(1+x^3)\sqrt{1-x^3}}dx$$$$letx={sin}^{\frac{2}{3}}ydx=\frac{2cos\left(y\right)}{3\sqrt[3]{siny}}dy$$$$=\int \frac{\sqrt[3]{sin\left(y\right)}}{(1+{sin}^2\left(y\right))cosy}.\frac{cos\left(y\right)}{\sqrt[3]{sin\left(y\right)}}dy$$$$=\frac{2}{3}\int \frac{1}{1+{sin}^2\left(y\right)}dy=\frac{2}{3}\int \frac{{csc}^2\left(y\right)}{{csc}^2\left(y\right)+1}dy$$$$=\frac{2}{3}\int \frac{{csc}^2\left(y\right)}{{cot}^2\left(y\right)+2}dy=\frac{\sqrt{2}}{3}{tan}^{-1}\left(\sqrt{2}tan\left(y\right)\right)+c$$$$=\frac{\sqrt{2}}{3}{tan}^{-1}\left(\frac{\sqrt{2}{x}^{\frac{3}{2}}}{\sqrt{1-x^3}}\right)+c$$

Answered by Sourav mridha last updated on 04/Jun/20

$$\left(2\right)..\mathit{l}\mathit{e}\mathit{t},\mathit{x}={\mathit{t}\mathit{a}\mathit{n}}^{\frac{2}{3}}\mathit{\alpha }\mathit{s}\mathit{o}\mathit{w}\mathit{e}\mathit{g}\mathit{e}\mathit{t}..$$$$=\frac{1}{6}\int \mathit{s}\mathit{e}\mathit{c}\left(2\mathit{\alpha }\right)\mathit{d}\left(2\mathit{\alpha }\right)+\frac{\mathit{\alpha }}{3}+\mathit{c}$$$$=\frac{1}{6}\mathit{l}\mathit{n}[\mathrm{t}\mathit{a}\mathit{n}(\frac{\mathit{\pi }}{4}+{\tan }^{-1}\left({\mathit{x}}^{\frac{3}{2}}\right)]$$$$+\frac{1}{3}{\tan }^{-1}\left({\mathit{x}}^{\frac{3}{2}}\right)+\mathit{c}$$$$0\mathit{r}\mathit{A}\mathit{n}\mathit{s}:$$$$=\mathit{l}\mathit{n}{\left[\frac{1+{\mathit{x}}^{\frac{3}{2}}}{1-{\mathit{x}}^{\frac{3}{2}}}\right]}^{\frac{1}{6}}+\frac{1}{3}{\tan }^{-1}\left({\mathit{x}}^{\frac{3}{2}}\right)+\mathit{c}$$

Answered by  M±th+et+s last updated on 04/Jun/20

$$=\int \frac{\sqrt{x}}{x^3(x^{-3}-1)\sqrt{x^3}\sqrt{x^{-3}+1}}dx$$$$=\frac{1}{2}\int \frac{x^{-4}}{(x^{-3}+1)\sqrt{x^{-3}+1}}dx$$$$=\int \frac{1}{\frac{x^{-3}+1}{2}-1}.\frac{x^{-4}}{2\sqrt{x^{-3}+1}}dx$$$$=\int \frac{1}{1-{\left(\sqrt{\frac{x^{-3}+1}{2}}\right)}^2}.\frac{-x^{-4}}{2\sqrt{x^{-3}+1}}dx$$$$=\frac{\sqrt{2}}{3}{tanh}^{-1}\left(\sqrt{\frac{x^{-3}+1}{2}}\right)+c$$

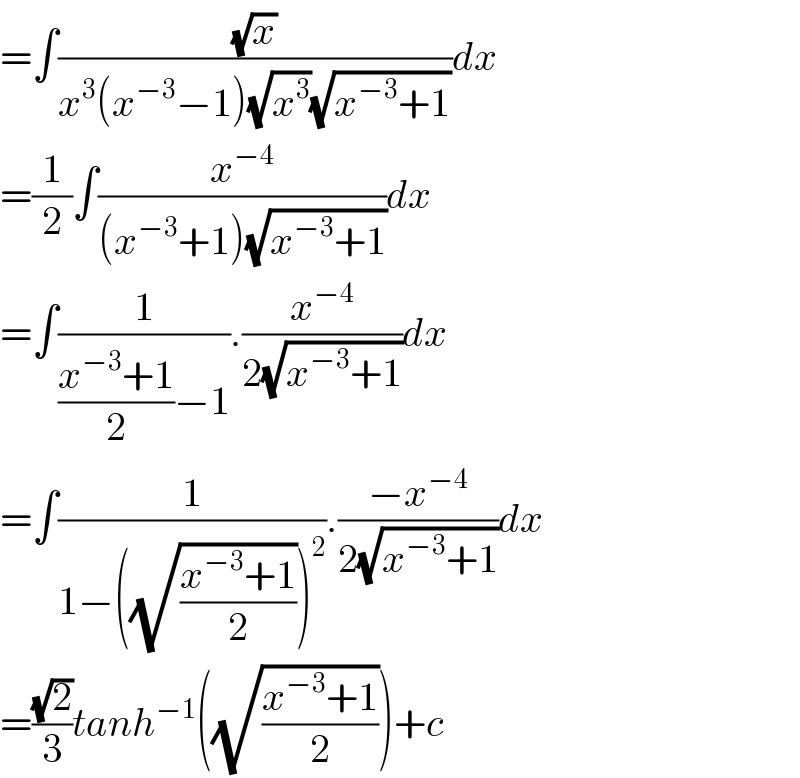
Commented by MJS last updated on 05/Jun/20

$$\mathrm{great}!$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com