
Question and Answers Forum
Question Number 96925 by M±th+et+s last updated on 05/Jun/20

Answered by mathmax by abdo last updated on 06/Jun/20
![let f(α) =∫_0 ^1 ((ln(x^2 +α))/(x+1))dx we have f(1) =∫_0 ^1 ((ln(x^2 +1))/(x+1))dx (α>0) f^′ (α) = ∫_0 ^1 (dx/((x^2 +α)(x+1))) let decompose F(x) =(1/((x+1)(x^2 +α))) F(x) =(a/(x+1)) +((bx+c)/(x^2 +α)) we have a =(1/(1+α)) lim_(x→+∞) xF(x) =0 =a+b ⇒b =−(1/(1+α)) F(0) =(1/α) =a+(c/α) ⇒1 =αa +c ⇒c =1−αa =1−(α/(1+α)) =(1/(1+α)) ⇒ F(x) =(1/((1+α)(x+1))) +((−(1/(1+α))x +(1/(1+α)))/(x^2 +α)) =(1/(1+α)){ (1/(x+1))−(x/(x^2 +α)) +(1/(x^2 +α))} ⇒ ∫ F(x) =(1/(1+α)){ln∣x+1∣−(1/2)ln(x^2 +α) +∫ (dx/(x^2 +α))} ∫ (dx/(x^2 +α)) =_(x =(√α)u) ∫ (((√α)du)/(α(1+u^2 ))) =(1/(√α)) arctan((x/(√α))) ⇒ ∫_0 ^1 F(x)dx =(1/(1+α)){ [ln∣((x+1)/(√(x^2 +α)))∣]_0 ^1 +[(1/(√α)) arctan((x/(√α)))]_0 ^1 } =(1/(1+α)){ ln((2/(√(1+α))))−ln((1/(√α))) +(1/(√α)) arctan((1/(√α)))} ⇒ f(α) =∫ ((ln((2/((√(1+α)) ))))/(1+α)) dα +(1/2)∫ ((lnα)/(1+α))dα +∫ ((arctan((1/(√α))))/((1+α)(√α))) dα +c ...be continued....](Q97188.png)
Answered by mathmax by abdo last updated on 07/Jun/20
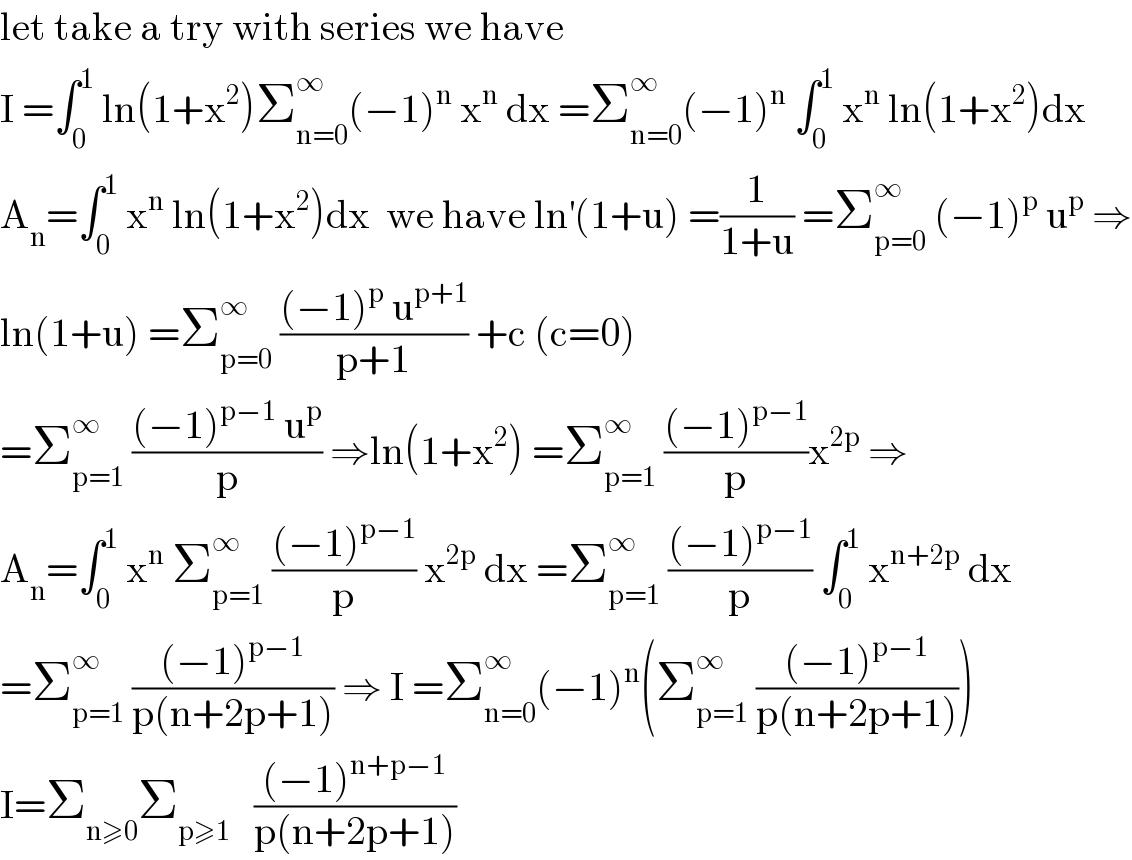
Commented by M±th+et+s last updated on 07/Jun/20

| ||
Question and Answers Forum | ||
Question Number 96925 by M±th+et+s last updated on 05/Jun/20 | ||
 | ||
Answered by mathmax by abdo last updated on 06/Jun/20 | ||
![let f(α) =∫_0 ^1 ((ln(x^2 +α))/(x+1))dx we have f(1) =∫_0 ^1 ((ln(x^2 +1))/(x+1))dx (α>0) f^′ (α) = ∫_0 ^1 (dx/((x^2 +α)(x+1))) let decompose F(x) =(1/((x+1)(x^2 +α))) F(x) =(a/(x+1)) +((bx+c)/(x^2 +α)) we have a =(1/(1+α)) lim_(x→+∞) xF(x) =0 =a+b ⇒b =−(1/(1+α)) F(0) =(1/α) =a+(c/α) ⇒1 =αa +c ⇒c =1−αa =1−(α/(1+α)) =(1/(1+α)) ⇒ F(x) =(1/((1+α)(x+1))) +((−(1/(1+α))x +(1/(1+α)))/(x^2 +α)) =(1/(1+α)){ (1/(x+1))−(x/(x^2 +α)) +(1/(x^2 +α))} ⇒ ∫ F(x) =(1/(1+α)){ln∣x+1∣−(1/2)ln(x^2 +α) +∫ (dx/(x^2 +α))} ∫ (dx/(x^2 +α)) =_(x =(√α)u) ∫ (((√α)du)/(α(1+u^2 ))) =(1/(√α)) arctan((x/(√α))) ⇒ ∫_0 ^1 F(x)dx =(1/(1+α)){ [ln∣((x+1)/(√(x^2 +α)))∣]_0 ^1 +[(1/(√α)) arctan((x/(√α)))]_0 ^1 } =(1/(1+α)){ ln((2/(√(1+α))))−ln((1/(√α))) +(1/(√α)) arctan((1/(√α)))} ⇒ f(α) =∫ ((ln((2/((√(1+α)) ))))/(1+α)) dα +(1/2)∫ ((lnα)/(1+α))dα +∫ ((arctan((1/(√α))))/((1+α)(√α))) dα +c ...be continued....](Q97188.png) | ||
| ||
Answered by mathmax by abdo last updated on 07/Jun/20 | ||
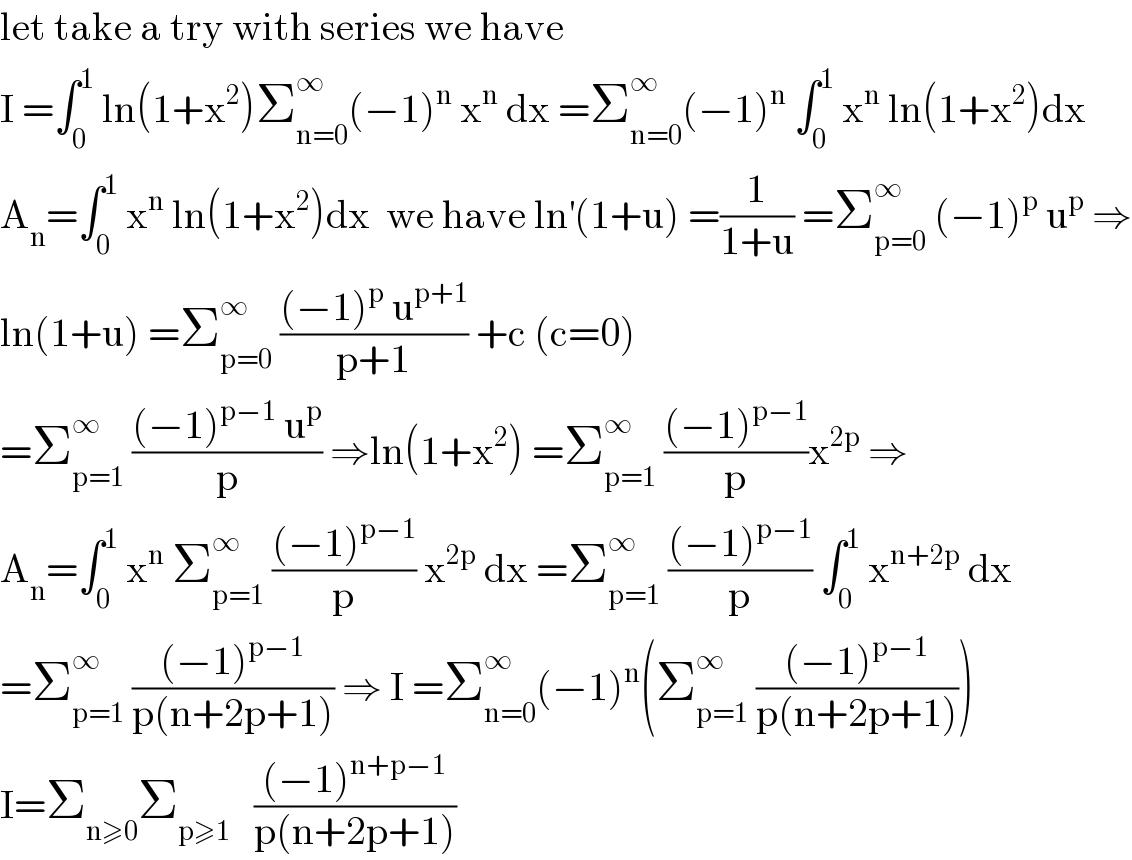 | ||
| ||
Commented by M±th+et+s last updated on 07/Jun/20 | ||
 | ||