
Question and Answers Forum
Question Number 97041 by bemath last updated on 06/Jun/20
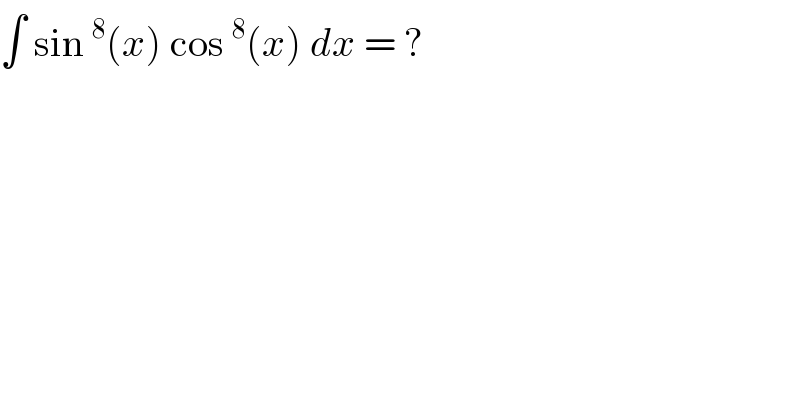
Answered by john santu last updated on 06/Jun/20
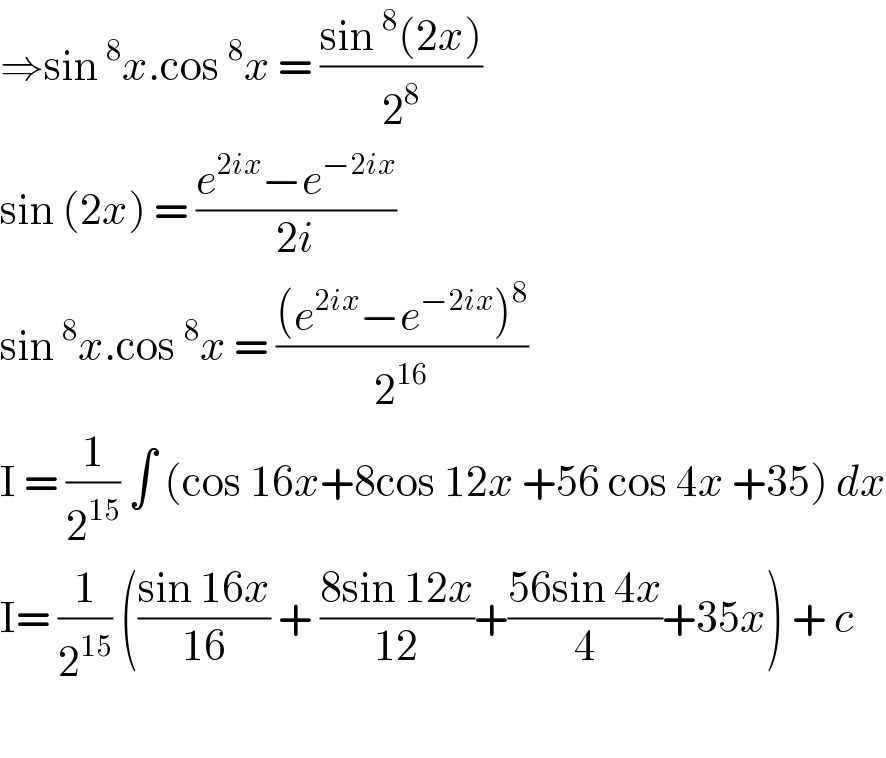
Answered by Sourav mridha last updated on 06/Jun/20
![let sinx=m ∫(1−m^2 )^7 m^8 dm =∫[Σ_(r=0) ^7 C_r ^7 (1)^(7−r) .(−m^2 )^r .].m^8 dm =Σ_(r=0) ^7 (−1)^r C_r ^7 [∫m^(2r+8) dm] =Σ_(r=0) ^7 (−1)^r C_r ^7 (((sin(x))^(2r+9) )/(2r+9)).+k](Q97046.png)
| ||
Question and Answers Forum | ||
Question Number 97041 by bemath last updated on 06/Jun/20 | ||
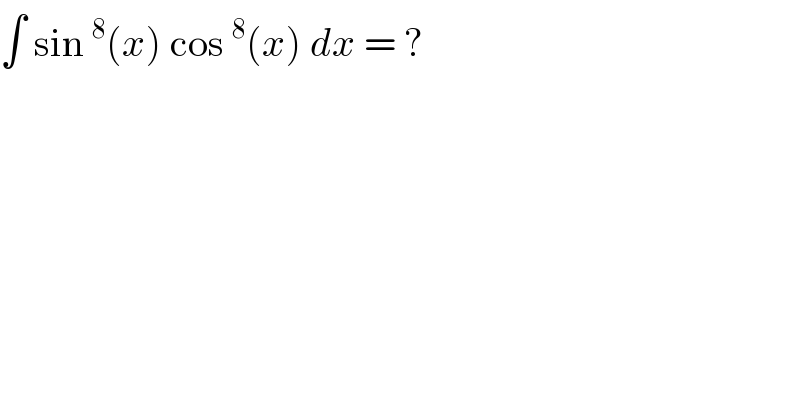 | ||
Answered by john santu last updated on 06/Jun/20 | ||
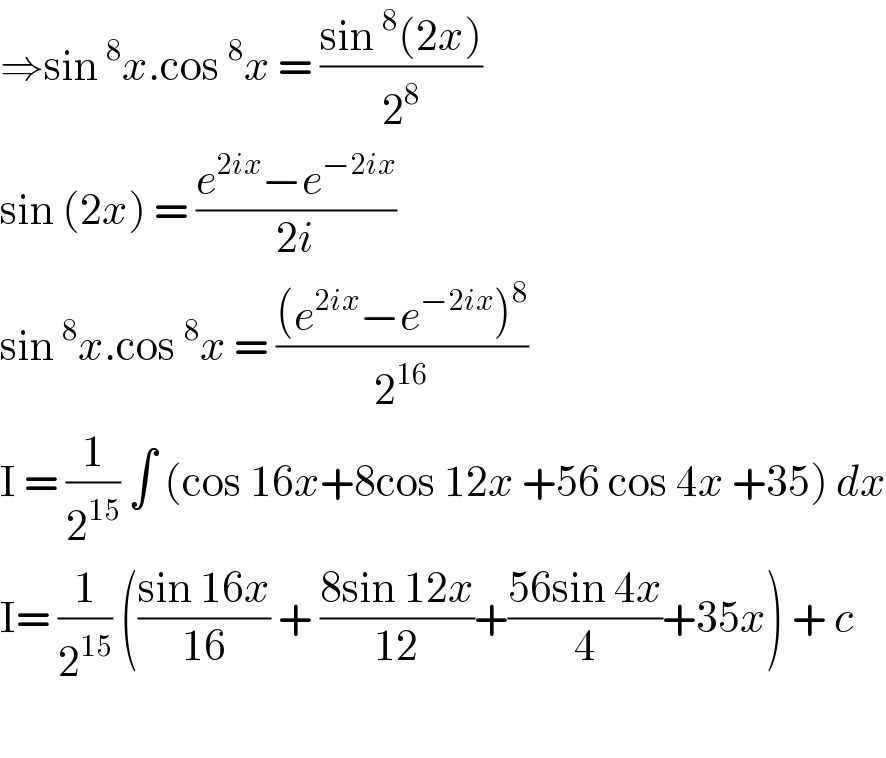 | ||
| ||
Answered by Sourav mridha last updated on 06/Jun/20 | ||
![let sinx=m ∫(1−m^2 )^7 m^8 dm =∫[Σ_(r=0) ^7 C_r ^7 (1)^(7−r) .(−m^2 )^r .].m^8 dm =Σ_(r=0) ^7 (−1)^r C_r ^7 [∫m^(2r+8) dm] =Σ_(r=0) ^7 (−1)^r C_r ^7 (((sin(x))^(2r+9) )/(2r+9)).+k](Q97046.png) | ||
| ||