Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 97136 by I want to learn more last updated on 06/Jun/20

$$\mathrm{Evaluate}$$$$\frac{3}{1!+2!+3!}+\frac{4}{2!+3!+4!}+...+\frac{2001}{1999!+2000!+2001!}$$

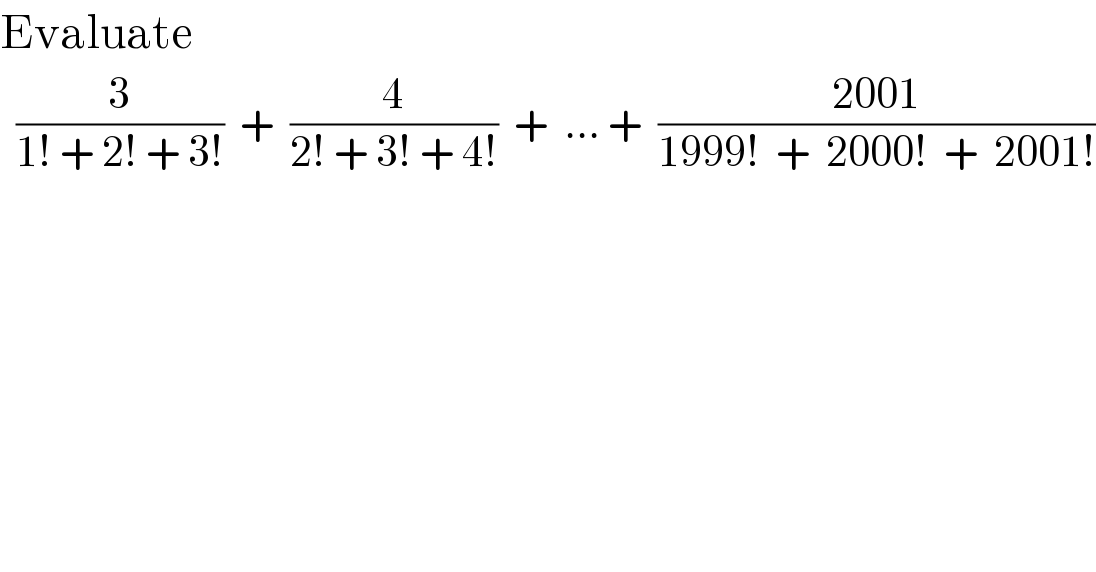
Commented by 06122004 last updated on 06/Jun/20

$$\ast Yechim\ast$$$$n!+(n+1)!+(n+2)!=n!(1+(n+1)+(n+1)(n+2))=$$$$=n!\ast {(n+2)}^2⊛$$$$\frac{3}{1!\ast 3^2}+\frac{4}{2!\ast 4^2}+...+\frac{2001}{1999!\ast {2001}^2}=$$$$=\frac{1}{1!\ast 3}+\frac{1}{2!\ast 4}+...+\frac{1}{1999!\ast 2001}=$$$$=\frac{2}{3!}+\frac{3}{4!}+...+\frac{2000}{2001!}=$$$$=\frac{3-1}{3!}+\frac{4-1}{4!}+...+\frac{2001-1}{2001!}=$$$$=\frac{1}{2!}-\frac{1}{3!}+\frac{1}{3!}-\frac{1}{4!}+...+\frac{1}{2000!}-\frac{1}{2001!}=$$$$=\frac{1}{2!}-\frac{1}{2001!}=\frac{\frac{2001!}{2}-1}{2001!}=\frac{2001!-2}{2\ast 2001!}▴$$$$\ast Javob\ast \frac{2001!-2}{2\ast 2001!}$$$$AbdullaxatovJasurbek$$

Commented by I want to learn more last updated on 06/Jun/20

$$\mathrm{Thanks}\mathrm{sir}.$$

Commented by 06122004 last updated on 06/Jun/20

$$ok!$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com