
Question and Answers Forum
Question Number 97218 by bobhans last updated on 07/Jun/20
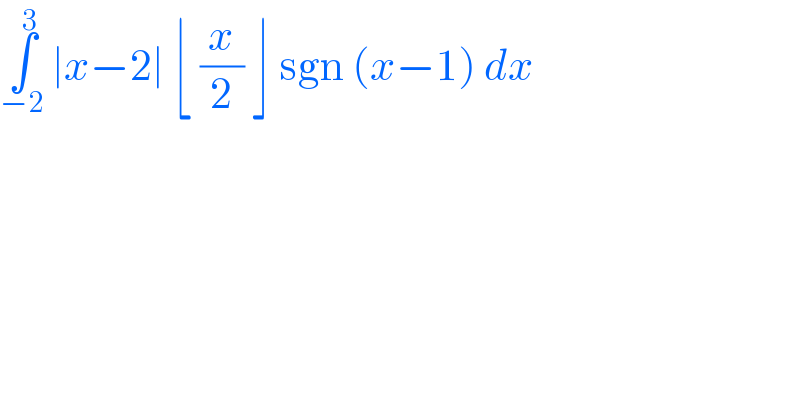
Answered by john santu last updated on 07/Jun/20
![sgn(x−1)=1 , when x>1 sgn(x−1)=−1, when x<1 J= −∫_(−2) ^1 ∣x−2∣ ⌊ (x/2) ⌋ dx + ∫_1 ^3 ∣x−2∣ ⌊ (x/2) ⌋ dx J = ∫_(−2) ^1 (x−2) ⌊(x/2)⌋ dx− ∫_1 ^2 (x−2) ⌊(x/2)⌋ dx + ∫_2 ^3 (x−2) ⌊(x/2)⌋ dx J= ∫_(−2) ^3 (x−2)⌊(x/2)⌋dx−2∫_1 ^2 (x−2) ⌊(x/2)⌋ dx let x=2z J=∫_(−1) ^(3/2) (2z−2)⌊z⌋.2 dz−2∫_(1/2) ^1 (2z−2)⌊z⌋.2dz J=∫_(−1) ^(3/2) (4z−4)⌊z⌋ dz−∫_(1/2) ^1 (8z−8)⌊z⌋ dz J=∫_(−1) ^0 (4−4z)dz + ∫_1 ^(3/2) (4z−4)dz J=[(4z−2z^2 )]_(−1) ^( 0) + [(2z^2 −4z)]_( 1) ^(3/2) J= 0−(−4−2)+2((9/4)−1)−4((3/2)−1) J = 6 + 2((5/4))−4((1/2)) J = 6 +(5/2)−2 = 4+(5/2) = ((13)/2)](Q97222.png)
Answered by mathmax by abdo last updated on 07/Jun/20
![A =∫_(−2) ^3 ∣x−2∣[(x/2)]δ(x−1) dx with δ(x−1) =1 if x>1 and δ(x−1)=−1if x<1 changement (x/2) =t give A =∫_(−1) ^(3/2) ∣2t−2∣[t]δ(2t−1)2dt =4 ∫_(−1) ^(3/2) ∣t−1∣ [t]δ(2t−1)dt =4 ( ∫_(−1) ^0 (1−t)(−1)(−1)dt +∫_0 ^(1/2) (1−t)0 (−1)dt +∫_(1/2) ^1 (1−t)0(1)dt +∫_1 ^(3/2) (t−1)1dt) =4( ∫_(−1) ^0 (1−t)dt +∫_1 ^(3/2) (t−1)dt) =4{ [t−(t^2 /2)]_(−1) ^0 +[ (t^2 /2)−t]_1 ^(3/2) } =4{ −(−1−(1/2))+(9/8)−(3/2)−(−(1/2))} =4{(9/8) +(1/2)} =(9/2) +2 =((13)/2)](Q97228.png)
| ||
Question and Answers Forum | ||
Question Number 97218 by bobhans last updated on 07/Jun/20 | ||
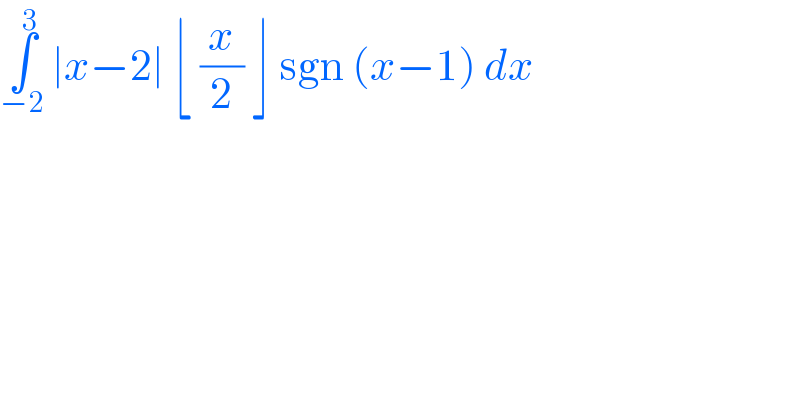 | ||
Answered by john santu last updated on 07/Jun/20 | ||
![sgn(x−1)=1 , when x>1 sgn(x−1)=−1, when x<1 J= −∫_(−2) ^1 ∣x−2∣ ⌊ (x/2) ⌋ dx + ∫_1 ^3 ∣x−2∣ ⌊ (x/2) ⌋ dx J = ∫_(−2) ^1 (x−2) ⌊(x/2)⌋ dx− ∫_1 ^2 (x−2) ⌊(x/2)⌋ dx + ∫_2 ^3 (x−2) ⌊(x/2)⌋ dx J= ∫_(−2) ^3 (x−2)⌊(x/2)⌋dx−2∫_1 ^2 (x−2) ⌊(x/2)⌋ dx let x=2z J=∫_(−1) ^(3/2) (2z−2)⌊z⌋.2 dz−2∫_(1/2) ^1 (2z−2)⌊z⌋.2dz J=∫_(−1) ^(3/2) (4z−4)⌊z⌋ dz−∫_(1/2) ^1 (8z−8)⌊z⌋ dz J=∫_(−1) ^0 (4−4z)dz + ∫_1 ^(3/2) (4z−4)dz J=[(4z−2z^2 )]_(−1) ^( 0) + [(2z^2 −4z)]_( 1) ^(3/2) J= 0−(−4−2)+2((9/4)−1)−4((3/2)−1) J = 6 + 2((5/4))−4((1/2)) J = 6 +(5/2)−2 = 4+(5/2) = ((13)/2)](Q97222.png) | ||
| ||
Answered by mathmax by abdo last updated on 07/Jun/20 | ||
![A =∫_(−2) ^3 ∣x−2∣[(x/2)]δ(x−1) dx with δ(x−1) =1 if x>1 and δ(x−1)=−1if x<1 changement (x/2) =t give A =∫_(−1) ^(3/2) ∣2t−2∣[t]δ(2t−1)2dt =4 ∫_(−1) ^(3/2) ∣t−1∣ [t]δ(2t−1)dt =4 ( ∫_(−1) ^0 (1−t)(−1)(−1)dt +∫_0 ^(1/2) (1−t)0 (−1)dt +∫_(1/2) ^1 (1−t)0(1)dt +∫_1 ^(3/2) (t−1)1dt) =4( ∫_(−1) ^0 (1−t)dt +∫_1 ^(3/2) (t−1)dt) =4{ [t−(t^2 /2)]_(−1) ^0 +[ (t^2 /2)−t]_1 ^(3/2) } =4{ −(−1−(1/2))+(9/8)−(3/2)−(−(1/2))} =4{(9/8) +(1/2)} =(9/2) +2 =((13)/2)](Q97228.png) | ||
| ||