hello every one why do planets of the solar system revolve around the sun in an eliptical not circular orbit


Question and Answers Forum

All Questions Topic List
Matrices and Determinants Questions
Previous in All Question Next in All Question
Previous in Matrices and Determinants Next in Matrices and Determinants
Question Number 97271 by M±th+et+s last updated on 07/Jun/20

$h e l l o e v e r y o n e$ $w h y d o p l a n e t s o f t h e s o l a r s y s t e m$ $r e v o l v e a r o u n d t h e s u n i n a n e l i p t i c a l$ $n o t c i r c u l a r o r b i t$
Commented by mr W last updated on 07/Jun/20

$i f w e h a d a t w o - b o d y s y s t e m$ $c o n s i s t i n g o f t h e s u n a n d a p l a n e t$ $a n d t h e o n l y f o r c e a c t i n g b e t w e e n$ $t h e m i s t h e g r a v i t a t i o n a l f o r c e a n d$ $b o t h o b j e c t s a r e s e e n a s p o i n t m a s s e s,$ $i t c a n b e p r o v e d t h a t t h e o r b i t o f t h e$ $p l a n e t a r o u n d t h e s u n i s a n e l l i p s e .$ $t h e s h a p e o f t h e e l l i p s e d e p e n t s o n$ $t h e i n i t i a l c o n d i t i o n . i n s p e c i a l$ $c o n d i t i o n, t h e o r b i t c a n b e a c i r c l e$ $w h i c h i s a l s o a s p e c i a l f o r m o f e l l i p s e .$ $b u t t h e r e a l s o l a r s y s t e m i s m u c h m o r e$ $c o m p l i c a t e d t h a n a t w o - b o d y s y s t e m,$ $t h e r e a r e s e v e r a l p l a n e t s w h i c h$ $a f f e c t e a c h o t h e r a n d b o t h t h e s u n$ $a n d t h e p l a n e t s a r e n o t p o i n t m a s s e s,$ $t h e r e f o r e t h e r e a l o r b i t s o f t h e p l a n e t s$ $a r e n o t p e r f e c t e l l i p s e s, o n l y n e a r$ $e l l i p s e s . a c i r c u l a r o r b i t i s t o o p e r f e c t,$ $w h i c h c a n n o t b e k e p t s t a b l e i n n a t u r e,$ $b e c a u s e a n y d i s t u r b a n c e m a y l e t i t$ $l e a v e t h i s p e r f e c t f o r m . n e v e r t h e l e s s$ $t h e o r b i t o f V e n u s i s a l m o s t a c i r c l e .$
Commented by M±th+et+s last updated on 08/Jun/20

$t h a n k y o u s i r$
	Answered by Sourav mridha last updated on 07/Jun/20

	$o k k {l e t}^{'} s s e e t h e t r a j e c t o r y o f$ $b o d y m o v i n g i n c e n t r a l f o r c e$ $f i e l d . . . b u t H ere i a m n o t u s i n g$ $G T R . . only t h e p o i n t o f v i e w o f$ $o l d c l a s s i c a l c o n c e p t o f N e w t o n i a n$ $L a g r a n g i a n M e c h a n i c s .$ ${l e t}^{'} s p i c k u p t h e e x a m p l e o f$ $o u r s o l a r s y s t e m . . . . w h e r e s u n i s$ $a t t h e f o c u s a n d e a r t h m o v e s$ $r o u n d s u n i n a c c o u n t o f G r a v i t a t i o n a l f o r c e$ $f e i l d .$ $s o o u r L a g r a n g i a n c o n s t r a c t e d$ $i n p l a n e p o l a r c o o r d i n a t e l i k e t h a t$ $L = \frac{1}{2} [{(\overset{∙}{r})}^{2} + r^{2} {(\overset{∙}{θ})}^{2}] - v (r)$ $n o w u s i n g E u l e r - L a g r a n g e {e q}^{n}$ $(f r o m V a r i a t i o n a l c a l c u l a s)$ $\frac{\partial L}{\partial r} - \frac{d}{d t} (\frac{\partial L}{\partial \overset{∙}{r}}) = 0 a n d \frac{\partial L}{\partial θ} - \frac{d}{d t} (\frac{\partial L}{\partial \overset{∙}{θ}}) = 0$ $f r o m 1 s t {e q}^{n} w e g et$ $\overset{∙ ∙}{r} - r {(\overset{∙}{θ})}^{2} = - \frac{\partial}{\partial r} [v (r)] = F (r) = \frac{k}{r^{2}}$ $. . . . . . . . . . . . . . . . . (i)$ $F (r) = g r a v i t e t i o n a l f o r c e, k = c o n s t a n t$ $k = {G m}_{s} m_{e} .$ $a n d 2 n d {e q}^{n} g i v e s u s$ $r^{2} \overset{∙}{θ} = c o n s t a n t, m u l t i : μ b o t h s i d e s$ $w e g e t L = μ r^{2} θ = c o n s t a n t$ $. . . . . . . . . . . (i i)$ $w h e r e μ = \frac{m_{s} m_{e}}{m_{s} + m_{e}} = r e d u c e m a s s$ $f o r c e n t r a l f o r c e -$ $t o r q u e τ = \vec{r} \times f (r) = 0 o r \frac{d L}{d t} = c o n s t a n t$ $w h e r e L = a n g u l a r m o m e n t a m .$ $n o w l e t u = \frac{1}{r} n o w d i f f w r t t o$ $θ a n d u s i n g {e q}^{n} (i i) w e g e t$ $\frac{d u}{d θ} = \frac{- 1}{r^{2}} . \frac{\frac{d r}{d t}}{\frac{d θ}{d t}} = - \frac{1}{r^{2}} \frac{\overset{∙}{r}}{\overset{∙}{θ}} = - \frac{μ}{L} \overset{∙}{r}$ $n o w \frac{d^{2} u}{d θ^{2}} = - \frac{μ^{2}}{L^{2} u^{2}} . \overset{∙ ∙}{r} .$ $s o w e g e t \overset{∙ ∙}{r} = - \frac{L^{2} u^{2}}{μ^{2}} . \frac{d^{2} u}{d θ^{2}} a n d$ $r {(\overset{∙}{θ})}^{2} = \frac{u^{3} L^{2}}{μ^{2}} . . .$ $n o w p u t t i n g t h i s t w o r e s u l t s a t$ ${e q}^{n} (i) w e g e t {e q}^{n} o f m o t i o n o f$ $e a r t h a r o u n d s u n i s$ $\frac{d^{2} u}{d θ^{2}} + u = - \frac{μ^{2} k}{L^{2}} (c o n s t a n t)$ $b y s o l v i n g t h i s e a s y 2 n d O D E$ $w e g e t u (θ) = - \frac{μ^{2} k}{L^{2}} + A c o s θ + B s i n θ$ $or = - \frac{μ^{2} k}{L^{2}} + γ c o s Φ$ $w e c o n s i d e r a t e a t f i r s t u = \frac{1}{r}$ $s o n o w r (Φ) = \frac{1}{- \frac{μ^{2} k}{L^{2}} + γ c o s (Φ)}$ $= \frac{- \frac{L^{2}}{μ^{2} k}}{1 - \frac{L^{2} γ}{μ^{2} k} c o s (Φ)}$ $c o m p a r e t h i s r e s u l t w i t h$ ${e q}^{n} o f a e l l i p s e i n p l a n e p o l a r$ $c o o r d i n a t e r (θ) = \frac{l}{1 \underline{+} e c o s (θ)}$ $i n o u r c a s e - -$ $s a m i l e t u s r e c t u m o f t h e e l l i p t i c a k$ $p a t h o f o u r p l a n e t i s$ $l = a (1 - e^{2}) = - \frac{L^{2}}{μ^{2} k}$ $a n d e s c e n t r i c i t y e = \frac{L^{2} γ}{μ^{2} k}$ $t h i s i s w h y p l a n e t s a r w m o v i n g$ $i n a e l l i p t i c a l p a t h . . .$ $1 s t p r o p o s e d b y K e p l e r i n h i s$ $1 s t l a s o f p l a n e t o r y m o t i o n . .$
	Commented by smridha last updated on 08/Jun/20

	$o h h s o r r y i t s h o u l d b e \frac{d L}{d t} = 0$ $s o L = c o n s t a n t .$
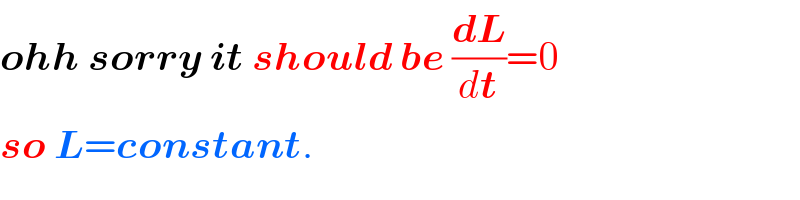
	Commented by M±th+et+s last updated on 08/Jun/20

	$g r e a t w o r k t h a n k s$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum