Question Number 97307 by eidmarie last updated on 07/Jun/20
Commented by john santu last updated on 07/Jun/20
$$\underset{\mathrm{1}} {\overset{\infty} {\int}}\:\left(\frac{\mathrm{ln}\left(\mathrm{5x}+\mathrm{n}\right)−\mathrm{ln}\left(\mathrm{n}\right)}{\mathrm{n}}\right)\:\mathrm{dx} \\ $$
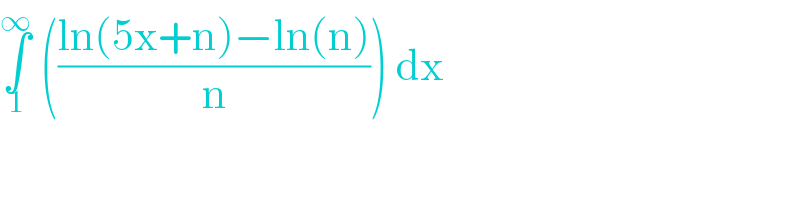
Commented by bemath last updated on 07/Jun/20
![[ x ln(5x+1)−x+(1/5)ln(5x+1)]_0 ^1 (ln(6)−1+(1/5)ln(6))−0 (6/5)ln(6)−1](Q97331.png)
$$\left[\:\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{ln}}\left(\mathrm{5}\boldsymbol{\mathrm{x}}+\mathrm{1}\right)−\boldsymbol{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{5}}\boldsymbol{\mathrm{ln}}\left(\mathrm{5}\boldsymbol{\mathrm{x}}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\left(\boldsymbol{\mathrm{ln}}\left(\mathrm{6}\right)−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5}}\boldsymbol{\mathrm{ln}}\left(\mathrm{6}\right)\right)−\mathrm{0} \\ $$$$\frac{\mathrm{6}}{\mathrm{5}}\boldsymbol{\mathrm{ln}}\left(\mathrm{6}\right)−\mathrm{1}\: \\ $$
Answered by Sourav mridha last updated on 07/Jun/20
![lim_(n→∞) (1/n)Σ_(k=1) ^n ln[((5k)/n)+1]=∫_0 ^1 ln(5x+1)dx](Q97326.png)
$$\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\boldsymbol{{n}}}\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\boldsymbol{{ln}}\left[\frac{\mathrm{5}\boldsymbol{{k}}}{\boldsymbol{{n}}}+\mathrm{1}\right]=\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{{ln}}\left(\mathrm{5}\boldsymbol{{x}}+\mathrm{1}\right)\boldsymbol{{dx}} \\ $$
Commented by ahmedeid last updated on 07/Jun/20
$${can}\:{you}\left[{solve}\left[{it}\left[{by}\left[{steps}\left[{sir}\right.\right.\right.\right.\right. \\ $$
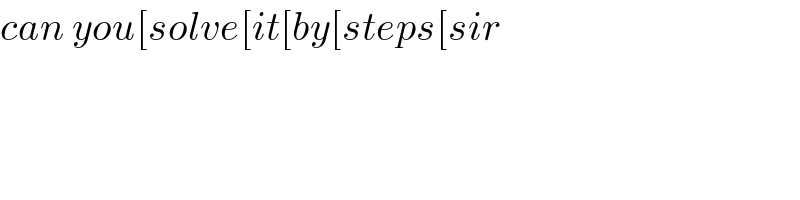
Commented by bemath last updated on 07/Jun/20
$$\mathrm{using}\:\mathrm{D}.\mathrm{I}\:\mathrm{method} \\ $$
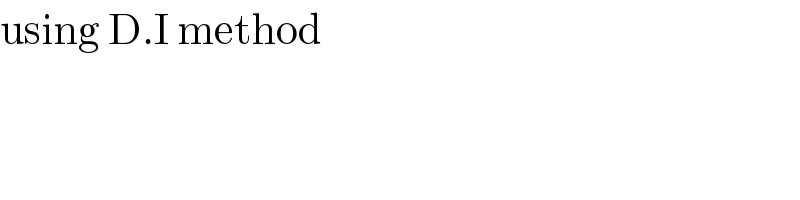
Commented by Sourav mridha last updated on 07/Jun/20
![∫_0 ^1 ln(5x+1)dx=(1/5)∫_0 ^1 ln(5x+1)d(5x+1) = =(1/5)[(5x+1){ln(5x+1)−1}]_0 ^1 =(1/5)[6(ln6−1)+1]](Q97332.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{{ln}}\left(\mathrm{5}\boldsymbol{{x}}+\mathrm{1}\right)\boldsymbol{{dx}}=\frac{\mathrm{1}}{\mathrm{5}}\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{{ln}}\left(\mathrm{5}\boldsymbol{{x}}+\mathrm{1}\right)\boldsymbol{{d}}\left(\mathrm{5}\boldsymbol{{x}}+\mathrm{1}\right) \\ $$$$=\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{5}}\left[\left(\mathrm{5}\boldsymbol{{x}}+\mathrm{1}\right)\left\{\boldsymbol{{ln}}\left(\mathrm{5}\boldsymbol{{x}}+\mathrm{1}\right)−\mathrm{1}\right\}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{5}}\left[\mathrm{6}\left(\boldsymbol{{ln}}\mathrm{6}−\mathrm{1}\right)+\mathrm{1}\right] \\ $$
Commented by ahmedeid last updated on 07/Jun/20
$${thanks}\left[{alot}\left[{sir}\right.\right. \\ $$
Commented by ahmedeid last updated on 07/Jun/20
Commented by ahmedeid last updated on 07/Jun/20
$${numbdr}\:\mathrm{14}\:{please} \\ $$
Commented by bemath last updated on 07/Jun/20
$$\mathrm{qn}\:\mathrm{97305} \\ $$
Commented by Sourav mridha last updated on 07/Jun/20
welcome
Answered by mathmax by abdo last updated on 08/Jun/20
![let S_n =Σ_(k=1) ^n (1/n)(ln(5k+n)−ln(n)) ⇒ S_n =(1/n) Σ_(k=1) ^n ln(((5k+n)/n)) =(1/n) Σ_(k=1) ^n ln(1+5(k/n))→∫_0 ^1 ln(1+5x)dx lim_(n→+∞) S_n =∫_0 ^1 ln(1+5x)dx changement ln(1+5x)=t give 1+5x =e^t ⇒x =((e^t −1)/5) ⇒∫_0 ^1 ln(1+5x)dx =∫_0 ^(ln6) t ((1/5))e^t dt =(1/5) ∫_0 ^(ln6) t e^t dt =(1/5){ [t e^t ]_0 ^(ln6) −∫_0 ^(ln6) e^t dt} =(1/5){6ln6 −[e^t ]_0 ^(ln6) } =(6/5)ln6 −(1/5)(6−1) =(6/5)ln6 −1](Q97419.png)
$$\mathrm{let}\:\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{n}}\left(\mathrm{ln}\left(\mathrm{5k}+\mathrm{n}\right)−\mathrm{ln}\left(\mathrm{n}\right)\right)\:\Rightarrow \\ $$$$\mathrm{S}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{ln}\left(\frac{\mathrm{5k}+\mathrm{n}}{\mathrm{n}}\right)\:=\frac{\mathrm{1}}{\mathrm{n}}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{5}\frac{\mathrm{k}}{\mathrm{n}}\right)\rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\mathrm{5x}\right)\mathrm{dx} \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{S}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{5x}\right)\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{ln}\left(\mathrm{1}+\mathrm{5x}\right)=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{1}+\mathrm{5x}\:=\mathrm{e}^{\mathrm{t}} \:\Rightarrow\mathrm{x}\:=\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{1}}{\mathrm{5}}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{5x}\right)\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{ln6}} \:\mathrm{t}\:\left(\frac{\mathrm{1}}{\mathrm{5}}\right)\mathrm{e}^{\mathrm{t}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\:\int_{\mathrm{0}} ^{\mathrm{ln6}} \:\mathrm{t}\:\mathrm{e}^{\mathrm{t}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{5}}\left\{\:\left[\mathrm{t}\:\mathrm{e}^{\mathrm{t}} \right]_{\mathrm{0}} ^{\mathrm{ln6}} \:−\int_{\mathrm{0}} ^{\mathrm{ln6}} \:\mathrm{e}^{\mathrm{t}} \:\mathrm{dt}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\left\{\mathrm{6ln6}\:−\left[\mathrm{e}^{\mathrm{t}} \right]_{\mathrm{0}} ^{\mathrm{ln6}} \right\}\:=\frac{\mathrm{6}}{\mathrm{5}}\mathrm{ln6}\:−\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{6}−\mathrm{1}\right)\:=\frac{\mathrm{6}}{\mathrm{5}}\mathrm{ln6}\:−\mathrm{1} \\ $$
Commented by bemath last updated on 08/Jun/20
$$\mathrm{yes}.\:\mathrm{we}\:\mathrm{answer}\:\mathrm{the}\:\mathrm{same} \\ $$