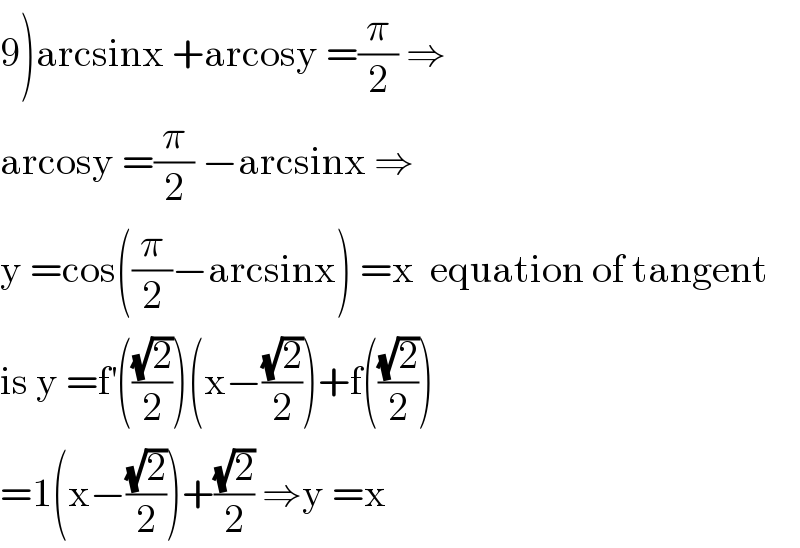Question and Answers Forum
Question Number 97353 by john santu last updated on 07/Jun/20

Answered by abdomathmax last updated on 07/Jun/20

Commented by john santu last updated on 08/Jun/20

Answered by abdomathmax last updated on 07/Jun/20
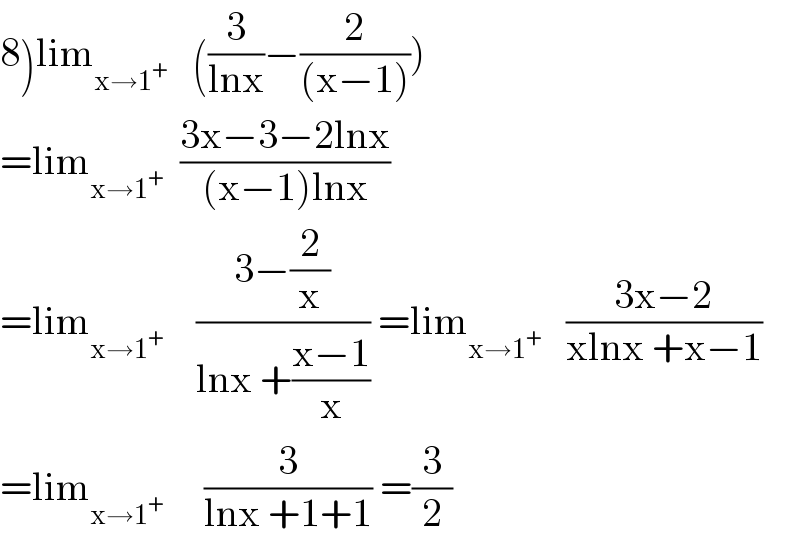
Answered by abdomathmax last updated on 07/Jun/20
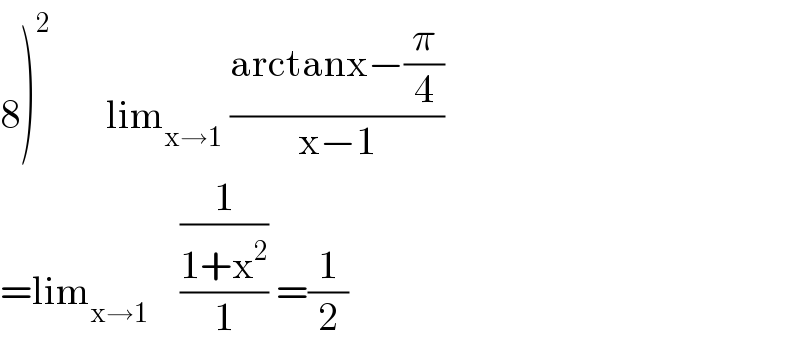
Answered by abdomathmax last updated on 07/Jun/20
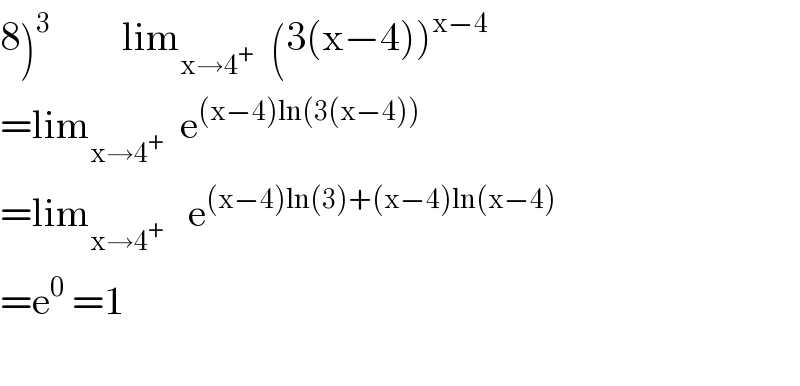
Answered by abdomathmax last updated on 07/Jun/20