
Question and Answers Forum
Question Number 97537 by M±th+et+s last updated on 08/Jun/20
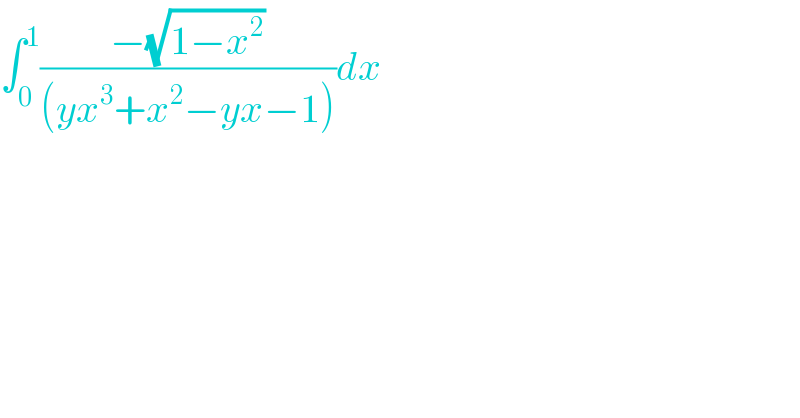
Answered by smridha last updated on 08/Jun/20
![∫_0 ^1 (dx/((yx+1)(√(1−x^2 )))) let x=sinA =∫_0 ^(𝛑/2) (dA/(ysinA+1))=2∫_0 ^(π/2) ((d(tan(A/2)+y))/((tan(A/2)+1)^2 +((√(1−y^2 )))^2 )) =2.(1/(√(1−y^2 )))[tan^(−1) (((tan(A/2)+y)/(√(1−y^2 ))))]_0 ^(𝛑/2) =(2/(√(1−y^2 )))[tan^(−1) (((1+y)/(√(1−y^2 ))))−tan^(−1) ((y/(√(1−y^2 )))) =(1/(√(1−y^2 )))tan^(−1) [(((1+y)(√(1−y^2 )))/y)]](Q97570.png)
Commented by M±th+et+s last updated on 08/Jun/20

Commented by smridha last updated on 08/Jun/20
welcome
| ||
Question and Answers Forum | ||
Question Number 97537 by M±th+et+s last updated on 08/Jun/20 | ||
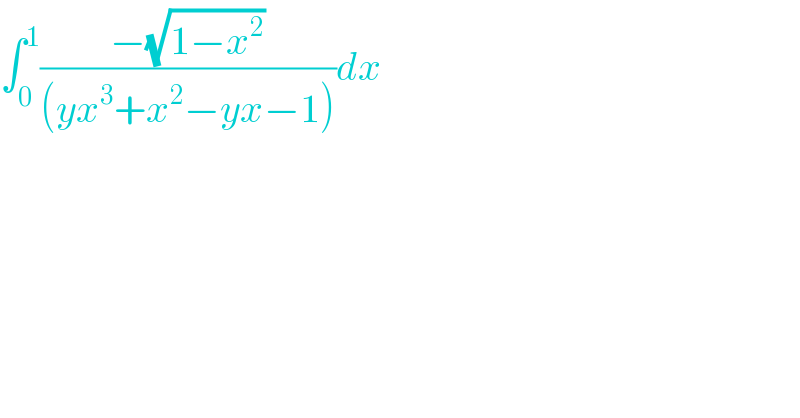 | ||
Answered by smridha last updated on 08/Jun/20 | ||
![∫_0 ^1 (dx/((yx+1)(√(1−x^2 )))) let x=sinA =∫_0 ^(𝛑/2) (dA/(ysinA+1))=2∫_0 ^(π/2) ((d(tan(A/2)+y))/((tan(A/2)+1)^2 +((√(1−y^2 )))^2 )) =2.(1/(√(1−y^2 )))[tan^(−1) (((tan(A/2)+y)/(√(1−y^2 ))))]_0 ^(𝛑/2) =(2/(√(1−y^2 )))[tan^(−1) (((1+y)/(√(1−y^2 ))))−tan^(−1) ((y/(√(1−y^2 )))) =(1/(√(1−y^2 )))tan^(−1) [(((1+y)(√(1−y^2 )))/y)]](Q97570.png) | ||
| ||
Commented by M±th+et+s last updated on 08/Jun/20 | ||
 | ||
Commented by smridha last updated on 08/Jun/20 | ||
welcome | ||