Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 97624 by mathmax by abdo last updated on 08/Jun/20

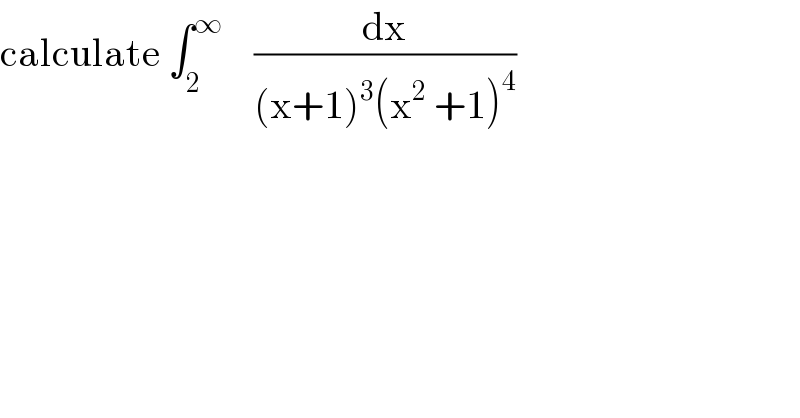
calculate ∫_2 ^∞ (dx/((x+1)^3 (x^2 +1)^4 ))

$$\mathrm{calculate}\:\int_{\mathrm{2}} ^{\infty} \:\:\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{4}} } \\ $$

Answered by MJS last updated on 09/Jun/20

∫(dx/((x+1)^3 (x^2 +1)^4 ))= [Ostrogradski] =−((45x^7 −6x^6 +37x^5 −16x^4 +−101x^3 −26x^2 −109x−32)/(192(x+1)^2 (x^2 +1)^3 ))−∫((15x−49)/(64(x+1)(x^2 +1)))dx −∫((15x−49)/(64(x+1)(x^2 +1)))dx=(1/2)∫(dx/(x+1))−∫((32x−17)/(64(x^2 +1)))dx= =(1/2)ln (x+1) −(1/4)ln (x^2 +1) +((17)/(64))arctan x = =(1/4)ln (((x+1)^2 )/(x^2 +1)) +((17)/(64))arctan x +C ∫_2 ^(+∞) (dx/((x+1)^3 (x^2 +1)^4 ))=((857)/(36000))+(1/4)ln (5/9) +((17)/(64))arctan (1/2)

$$\int\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}\right] \\ $$$$=−\frac{\mathrm{45}{x}^{\mathrm{7}} −\mathrm{6}{x}^{\mathrm{6}} +\mathrm{37}{x}^{\mathrm{5}} −\mathrm{16}{x}^{\mathrm{4}} +−\mathrm{101}{x}^{\mathrm{3}} −\mathrm{26}{x}^{\mathrm{2}} −\mathrm{109}{x}−\mathrm{32}}{\mathrm{192}\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }−\int\frac{\mathrm{15}{x}−\mathrm{49}}{\mathrm{64}\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx} \\ $$$$ \\ $$$$−\int\frac{\mathrm{15}{x}−\mathrm{49}}{\mathrm{64}\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}+\mathrm{1}}−\int\frac{\mathrm{32}{x}−\mathrm{17}}{\mathrm{64}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({x}+\mathrm{1}\right)\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)\:+\frac{\mathrm{17}}{\mathrm{64}}\mathrm{arctan}\:{x}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} +\mathrm{1}}\:+\frac{\mathrm{17}}{\mathrm{64}}\mathrm{arctan}\:{x}\:+{C} \\ $$$$ \\ $$$$\underset{\mathrm{2}} {\overset{+\infty} {\int}}\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }=\frac{\mathrm{857}}{\mathrm{36000}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\frac{\mathrm{5}}{\mathrm{9}}\:+\frac{\mathrm{17}}{\mathrm{64}}\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by I want to learn more last updated on 09/Jun/20

I appreciate sir.

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$

Commented by MJS last updated on 09/Jun/20

I explained Ostrogradski′s method a few weeks ago, cannot find the post now. there are explanations on the web

$$\mathrm{I}\:\mathrm{explained}\:\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{method}\:\mathrm{a}\:\mathrm{few} \\ $$$$\mathrm{weeks}\:\mathrm{ago},\:\mathrm{cannot}\:\mathrm{find}\:\mathrm{the}\:\mathrm{post}\:\mathrm{now}.\:\mathrm{there} \\ $$$$\mathrm{are}\:\mathrm{explanations}\:\mathrm{on}\:\mathrm{the}\:\mathrm{web} \\ $$

Commented by I want to learn more last updated on 09/Jun/20

Ohh. I wish you could find it sir, have missed

$$\mathrm{Ohh}.\:\mathrm{I}\:\mathrm{wish}\:\mathrm{you}\:\mathrm{could}\:\mathrm{find}\:\mathrm{it}\:\mathrm{sir},\:\mathrm{have}\:\mathrm{missed} \\ $$

Commented by MJS last updated on 09/Jun/20

question 94354

$${question}\:\mathrm{94354} \\ $$

Answered by mathmax by abdo last updated on 09/Jun/20

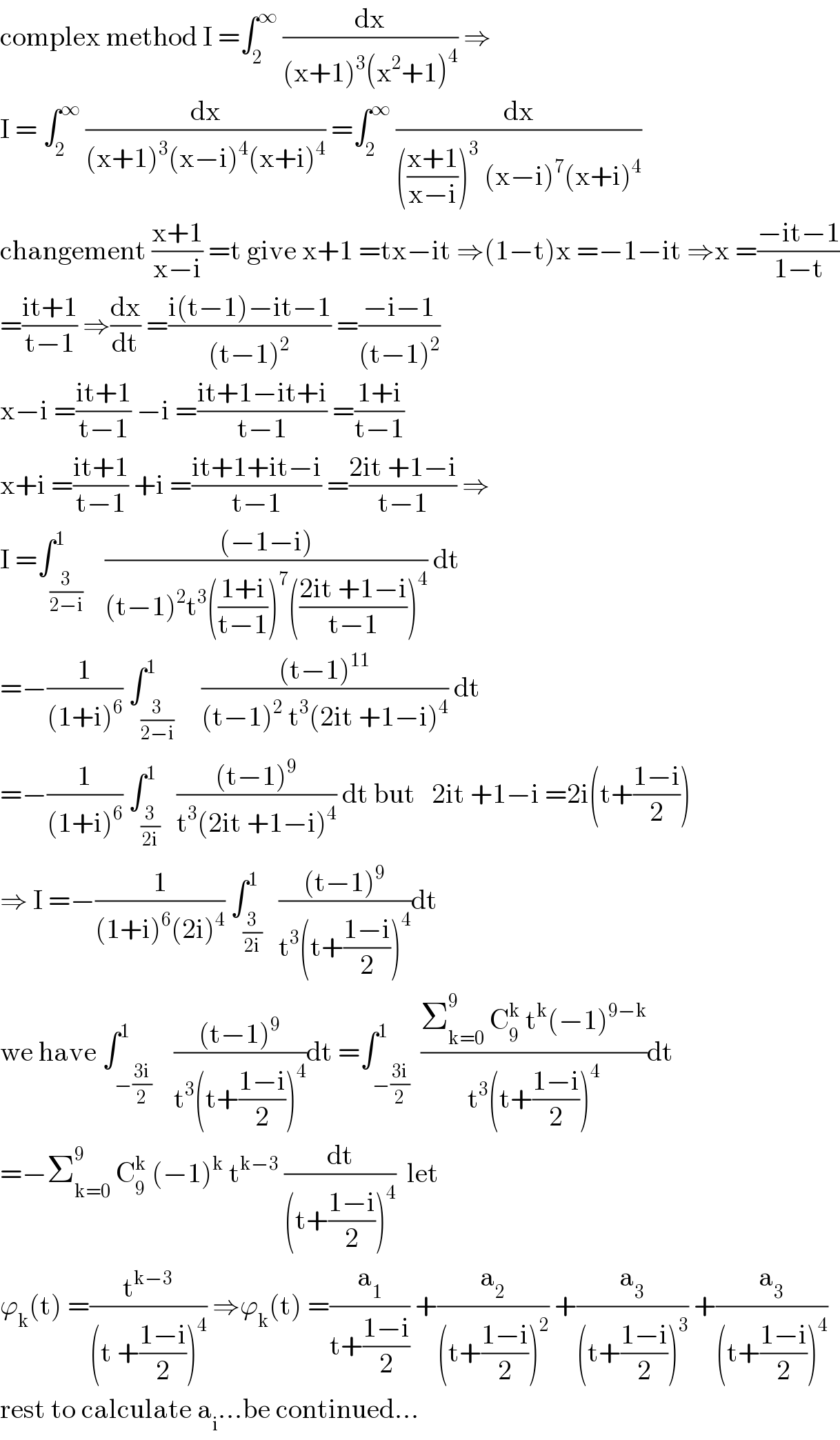
complex method I =∫_2 ^∞ (dx/((x+1)^3 (x^2 +1)^4 )) ⇒ I = ∫_2 ^∞ (dx/((x+1)^3 (x−i)^4 (x+i)^4 )) =∫_2 ^∞ (dx/((((x+1)/(x−i)))^3 (x−i)^7 (x+i)^4 )) changement ((x+1)/(x−i)) =t give x+1 =tx−it ⇒(1−t)x =−1−it ⇒x =((−it−1)/(1−t)) =((it+1)/(t−1)) ⇒(dx/dt) =((i(t−1)−it−1)/((t−1)^2 )) =((−i−1)/((t−1)^2 )) x−i =((it+1)/(t−1)) −i =((it+1−it+i)/(t−1)) =((1+i)/(t−1)) x+i =((it+1)/(t−1)) +i =((it+1+it−i)/(t−1)) =((2it +1−i)/(t−1)) ⇒ I =∫_(3/(2−i)) ^1 (((−1−i))/((t−1)^2 t^3 (((1+i)/(t−1)))^7 (((2it +1−i)/(t−1)))^4 )) dt =−(1/((1+i)^6 )) ∫_(3/(2−i)) ^1 (((t−1)^(11) )/((t−1)^2 t^3 (2it +1−i)^4 )) dt =−(1/((1+i)^6 )) ∫_(3/(2i)) ^1 (((t−1)^9 )/(t^3 (2it +1−i)^4 )) dt but 2it +1−i =2i(t+((1−i)/2)) ⇒ I =−(1/((1+i)^6 (2i)^4 )) ∫_(3/(2i)) ^1 (((t−1)^9 )/(t^3 (t+((1−i)/2))^4 ))dt we have ∫_(−((3i)/2)) ^1 (((t−1)^9 )/(t^3 (t+((1−i)/2))^4 ))dt =∫_(−((3i)/2)) ^1 ((Σ_(k=0) ^9 C_9 ^k t^k (−1)^(9−k) )/(t^3 (t+((1−i)/2))^4 ))dt =−Σ_(k=0) ^9 C_9 ^k (−1)^k t^(k−3) (dt/((t+((1−i)/2))^4 )) let ϕ_k (t) =(t^(k−3) /((t +((1−i)/2))^4 )) ⇒ϕ_k (t) =(a_1 /(t+((1−i)/2))) +(a_2 /((t+((1−i)/2))^2 )) +(a_3 /((t+((1−i)/2))^3 )) +(a_3 /((t+((1−i)/2))^4 )) rest to calculate a_i ...be continued...

$$\mathrm{complex}\:\mathrm{method}\:\mathrm{I}\:=\int_{\mathrm{2}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }\:\Rightarrow \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{2}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}−\mathrm{i}\right)^{\mathrm{4}} \left(\mathrm{x}+\mathrm{i}\right)^{\mathrm{4}} }\:=\int_{\mathrm{2}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{i}}\right)^{\mathrm{3}} \:\left(\mathrm{x}−\mathrm{i}\right)^{\mathrm{7}} \left(\mathrm{x}+\mathrm{i}\right)^{\mathrm{4}} } \\ $$$$\mathrm{changement}\:\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{i}}\:=\mathrm{t}\:\mathrm{give}\:\mathrm{x}+\mathrm{1}\:=\mathrm{tx}−\mathrm{it}\:\Rightarrow\left(\mathrm{1}−\mathrm{t}\right)\mathrm{x}\:=−\mathrm{1}−\mathrm{it}\:\Rightarrow\mathrm{x}\:=\frac{−\mathrm{it}−\mathrm{1}}{\mathrm{1}−\mathrm{t}} \\ $$$$=\frac{\mathrm{it}+\mathrm{1}}{\mathrm{t}−\mathrm{1}}\:\Rightarrow\frac{\mathrm{dx}}{\mathrm{dt}}\:=\frac{\mathrm{i}\left(\mathrm{t}−\mathrm{1}\right)−\mathrm{it}−\mathrm{1}}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{−\mathrm{i}−\mathrm{1}}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{x}−\mathrm{i}\:=\frac{\mathrm{it}+\mathrm{1}}{\mathrm{t}−\mathrm{1}}\:−\mathrm{i}\:=\frac{\mathrm{it}+\mathrm{1}−\mathrm{it}+\mathrm{i}}{\mathrm{t}−\mathrm{1}}\:=\frac{\mathrm{1}+\mathrm{i}}{\mathrm{t}−\mathrm{1}} \\ $$$$\mathrm{x}+\mathrm{i}\:=\frac{\mathrm{it}+\mathrm{1}}{\mathrm{t}−\mathrm{1}}\:+\mathrm{i}\:=\frac{\mathrm{it}+\mathrm{1}+\mathrm{it}−\mathrm{i}}{\mathrm{t}−\mathrm{1}}\:=\frac{\mathrm{2it}\:+\mathrm{1}−\mathrm{i}}{\mathrm{t}−\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\frac{\mathrm{3}}{\mathrm{2}−\mathrm{i}}} ^{\mathrm{1}} \:\:\:\frac{\left(−\mathrm{1}−\mathrm{i}\right)}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{t}^{\mathrm{3}} \left(\frac{\mathrm{1}+\mathrm{i}}{\mathrm{t}−\mathrm{1}}\right)^{\mathrm{7}} \left(\frac{\mathrm{2it}\:+\mathrm{1}−\mathrm{i}}{\mathrm{t}−\mathrm{1}}\right)^{\mathrm{4}} }\:\mathrm{dt} \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{i}\right)^{\mathrm{6}} }\:\int_{\frac{\mathrm{3}}{\mathrm{2}−\mathrm{i}}} ^{\mathrm{1}} \:\:\:\:\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{11}} }{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{t}^{\mathrm{3}} \left(\mathrm{2it}\:+\mathrm{1}−\mathrm{i}\right)^{\mathrm{4}} }\:\mathrm{dt} \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{i}\right)^{\mathrm{6}} }\:\int_{\frac{\mathrm{3}}{\mathrm{2i}}} ^{\mathrm{1}} \:\:\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{9}} }{\mathrm{t}^{\mathrm{3}} \left(\mathrm{2it}\:+\mathrm{1}−\mathrm{i}\right)^{\mathrm{4}} }\:\mathrm{dt}\:\mathrm{but}\:\:\:\mathrm{2it}\:+\mathrm{1}−\mathrm{i}\:=\mathrm{2i}\left(\mathrm{t}+\frac{\mathrm{1}−\mathrm{i}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\mathrm{I}\:=−\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{i}\right)^{\mathrm{6}} \left(\mathrm{2i}\right)^{\mathrm{4}} }\:\int_{\frac{\mathrm{3}}{\mathrm{2i}}} ^{\mathrm{1}} \:\:\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{9}} }{\mathrm{t}^{\mathrm{3}} \left(\mathrm{t}+\frac{\mathrm{1}−\mathrm{i}}{\mathrm{2}}\right)^{\mathrm{4}} }\mathrm{dt} \\ $$$$\mathrm{we}\:\mathrm{have}\:\int_{−\frac{\mathrm{3i}}{\mathrm{2}}} ^{\mathrm{1}} \:\:\:\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{9}} }{\mathrm{t}^{\mathrm{3}} \left(\mathrm{t}+\frac{\mathrm{1}−\mathrm{i}}{\mathrm{2}}\right)^{\mathrm{4}} }\mathrm{dt}\:=\int_{−\frac{\mathrm{3i}}{\mathrm{2}}} ^{\mathrm{1}} \:\frac{\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{9}} \:\mathrm{C}_{\mathrm{9}} ^{\mathrm{k}} \:\mathrm{t}^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{9}−\mathrm{k}} }{\mathrm{t}^{\mathrm{3}} \left(\mathrm{t}+\frac{\mathrm{1}−\mathrm{i}}{\mathrm{2}}\right)^{\mathrm{4}} }\mathrm{dt} \\ $$$$=−\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{9}} \:\mathrm{C}_{\mathrm{9}} ^{\mathrm{k}} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{t}^{\mathrm{k}−\mathrm{3}} \:\frac{\mathrm{dt}}{\left(\mathrm{t}+\frac{\mathrm{1}−\mathrm{i}}{\mathrm{2}}\right)^{\mathrm{4}} }\:\:\mathrm{let} \\ $$$$\varphi_{\mathrm{k}} \left(\mathrm{t}\right)\:=\frac{\mathrm{t}^{\mathrm{k}−\mathrm{3}} }{\left(\mathrm{t}\:+\frac{\mathrm{1}−\mathrm{i}}{\mathrm{2}}\right)^{\mathrm{4}} }\:\Rightarrow\varphi_{\mathrm{k}} \left(\mathrm{t}\right)\:=\frac{\mathrm{a}_{\mathrm{1}} }{\mathrm{t}+\frac{\mathrm{1}−\mathrm{i}}{\mathrm{2}}}\:+\frac{\mathrm{a}_{\mathrm{2}} }{\left(\mathrm{t}+\frac{\mathrm{1}−\mathrm{i}}{\mathrm{2}}\right)^{\mathrm{2}} }\:+\frac{\mathrm{a}_{\mathrm{3}} }{\left(\mathrm{t}+\frac{\mathrm{1}−\mathrm{i}}{\mathrm{2}}\right)^{\mathrm{3}} }\:+\frac{\mathrm{a}_{\mathrm{3}} }{\left(\mathrm{t}+\frac{\mathrm{1}−\mathrm{i}}{\mathrm{2}}\right)^{\mathrm{4}} } \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{a}_{\mathrm{i}} ...\mathrm{be}\:\mathrm{continued}... \\ $$

Commented by I want to learn more last updated on 09/Jun/20

Thanks sir. Waiting sir

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{Waiting}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com