
Question and Answers Forum
Question Number 97627 by mathmax by abdo last updated on 08/Jun/20
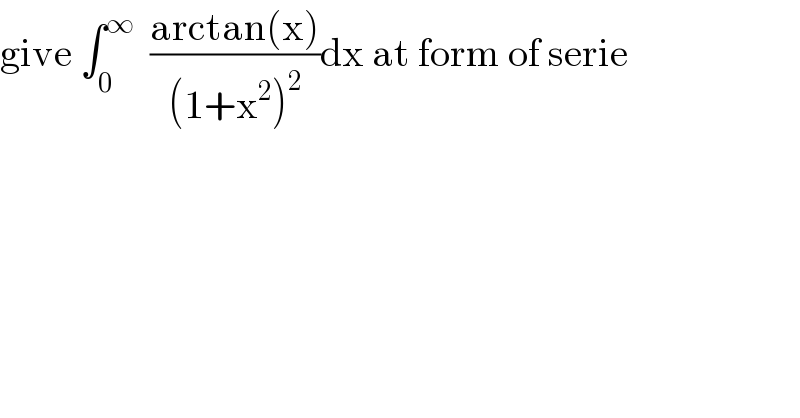
Answered by mathmax by abdo last updated on 09/Jun/20
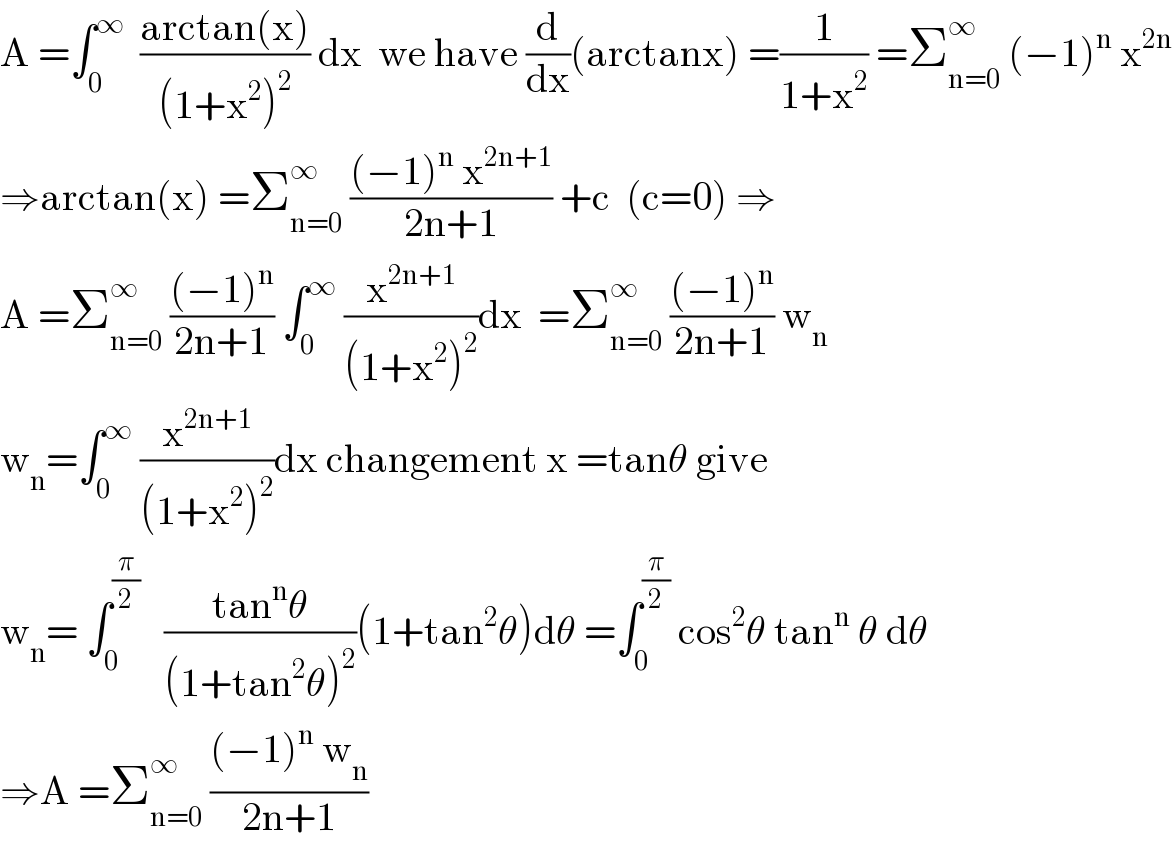
Answered by mathmax by abdo last updated on 09/Jun/20
![another way we have I =∫_0 ^∞ ((arctan(x))/((1+x^2 )^2 ))dx =∫_0 ^1 ((arctan(x))/((1+x^2 )^2 ))dx +∫_1 ^∞ ((arctan(x))/((1+x^2 )^2 ))dx(→x=(1/t)) =∫_0 ^1 ((arctan(x))/((1+x^2 )^2 ))dx +∫_0 ^1 (((π/2)−arctant)/((1+(1/t^2 ))^2 ))((dt/t^2 )) =∫_0 ^1 ((arctan(x))/((1+x^2 )^2 ))dx +∫_0 ^1 ((((π/2)−arctant)t^2 )/((1+t^2 )^2 ))dt =∫_0 ^1 ((arctan(x)+(π/2)x^2 −x^2 arctanx)/((1+x^2 )^2 ))dx =∫_0 ^1 (((1−x^2 )arctanx)/((1+x^2 )^2 )) +(π/2)∫_0 ^1 ((x^2 dx)/((1+x^2 )^2 )) we have for ∣u∣<1 (1/(1+u)) =Σ_(n=0) ^∞ (−1)^n u^n ⇒−(1/((1+u)^2 )) =Σ_(n=1) ^∞ n(−1)^n u^(n−1) ⇒(1/((1+u)^2 )) =Σ_(n=1) ^∞ n(−1)^(n−1) u^(n−1) =Σ_(n=0) ^∞ (n+1)(−1)^n u^n ⇒ (1/((1+x^2 )^2 )) =Σ_(n=0) ^∞ (n+1)(−1)^n x^(2n) ⇒ ∫_0 ^1 ((x^2 dx)/((1+x^2 )^2 )) =Σ_(n=0) ^∞ (n+1)(−1)^n ∫_0 ^1 x^(2n+2) dx =Σ_(n=0) ^∞ (((n+1)(−1)^n )/(2n+3)) ∫_0 ^1 (((1−x^2 )arctan(x))/((1+x^2 )^2 ))dx =Σ_(n=0) ^∞ (n+1)(−1)^n ∫_0 ^1 (1−x^2 )x^(2n) arctan(x)dx =Σ_(n=0) ^∞ (n+1)(−1)^n A_n with A_n =∫_0 ^1 (x^(2n) −x^(2n+2) )arctanx dx A_n =[((1/(2n+1))x^(2n+1) −(1/(2n+3))x^(2n+3) ) arctanx]_0 ^1 −∫_0 ^1 ((1/(2n+1))x^(2n+1) −(1/(2n+3))x^(2n+3) )(dx/(1+x^2 )) =(π/4)((1/(2n+1))−(1/(2n+3)))−(1/(2n+1))∫_0 ^1 (x^(2n+1) /(1+x^2 ))dx+(1/(2n+3)) ∫_0 ^1 (x^(2n+3) /(1+x^2 )) dx...be continued...](Q97722.png)
| ||
Question and Answers Forum | ||
Question Number 97627 by mathmax by abdo last updated on 08/Jun/20 | ||
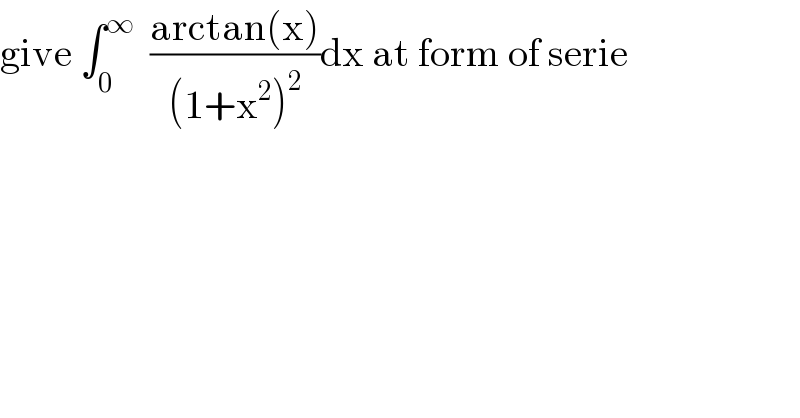 | ||
Answered by mathmax by abdo last updated on 09/Jun/20 | ||
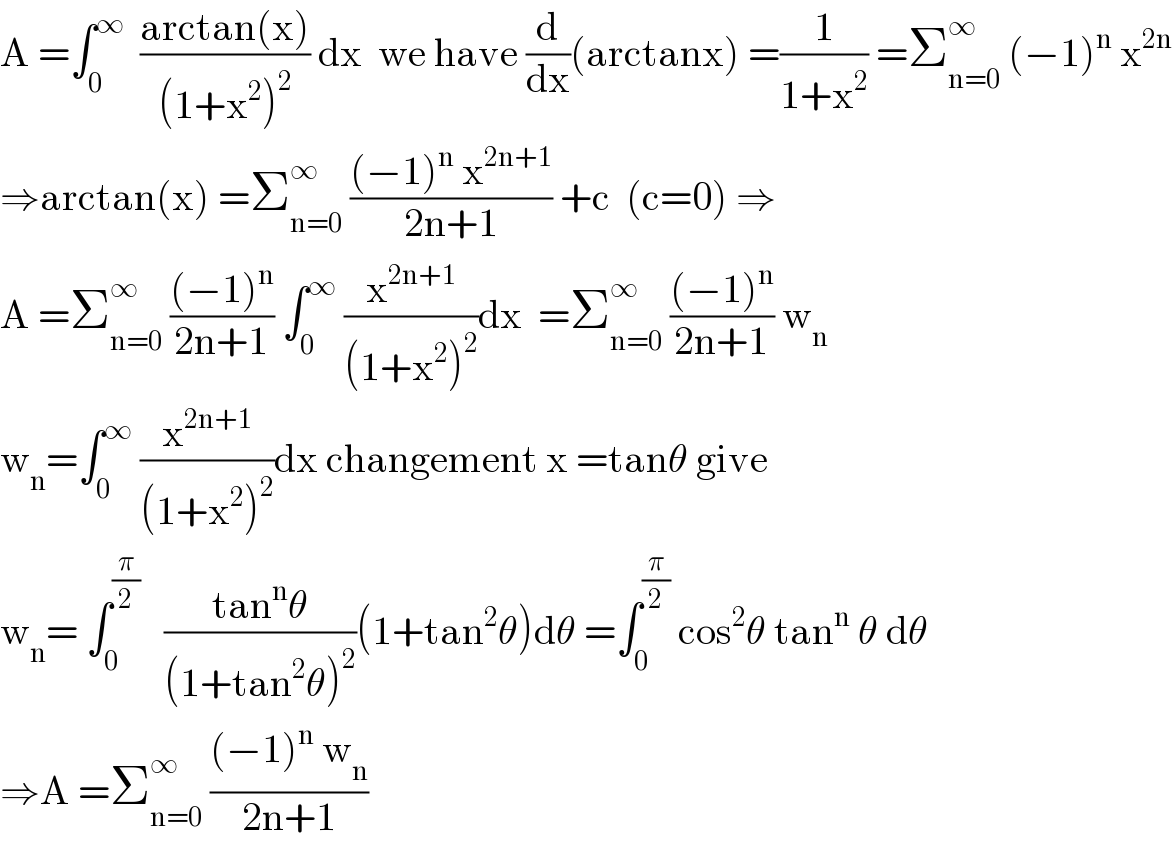 | ||
| ||
Answered by mathmax by abdo last updated on 09/Jun/20 | ||
![another way we have I =∫_0 ^∞ ((arctan(x))/((1+x^2 )^2 ))dx =∫_0 ^1 ((arctan(x))/((1+x^2 )^2 ))dx +∫_1 ^∞ ((arctan(x))/((1+x^2 )^2 ))dx(→x=(1/t)) =∫_0 ^1 ((arctan(x))/((1+x^2 )^2 ))dx +∫_0 ^1 (((π/2)−arctant)/((1+(1/t^2 ))^2 ))((dt/t^2 )) =∫_0 ^1 ((arctan(x))/((1+x^2 )^2 ))dx +∫_0 ^1 ((((π/2)−arctant)t^2 )/((1+t^2 )^2 ))dt =∫_0 ^1 ((arctan(x)+(π/2)x^2 −x^2 arctanx)/((1+x^2 )^2 ))dx =∫_0 ^1 (((1−x^2 )arctanx)/((1+x^2 )^2 )) +(π/2)∫_0 ^1 ((x^2 dx)/((1+x^2 )^2 )) we have for ∣u∣<1 (1/(1+u)) =Σ_(n=0) ^∞ (−1)^n u^n ⇒−(1/((1+u)^2 )) =Σ_(n=1) ^∞ n(−1)^n u^(n−1) ⇒(1/((1+u)^2 )) =Σ_(n=1) ^∞ n(−1)^(n−1) u^(n−1) =Σ_(n=0) ^∞ (n+1)(−1)^n u^n ⇒ (1/((1+x^2 )^2 )) =Σ_(n=0) ^∞ (n+1)(−1)^n x^(2n) ⇒ ∫_0 ^1 ((x^2 dx)/((1+x^2 )^2 )) =Σ_(n=0) ^∞ (n+1)(−1)^n ∫_0 ^1 x^(2n+2) dx =Σ_(n=0) ^∞ (((n+1)(−1)^n )/(2n+3)) ∫_0 ^1 (((1−x^2 )arctan(x))/((1+x^2 )^2 ))dx =Σ_(n=0) ^∞ (n+1)(−1)^n ∫_0 ^1 (1−x^2 )x^(2n) arctan(x)dx =Σ_(n=0) ^∞ (n+1)(−1)^n A_n with A_n =∫_0 ^1 (x^(2n) −x^(2n+2) )arctanx dx A_n =[((1/(2n+1))x^(2n+1) −(1/(2n+3))x^(2n+3) ) arctanx]_0 ^1 −∫_0 ^1 ((1/(2n+1))x^(2n+1) −(1/(2n+3))x^(2n+3) )(dx/(1+x^2 )) =(π/4)((1/(2n+1))−(1/(2n+3)))−(1/(2n+1))∫_0 ^1 (x^(2n+1) /(1+x^2 ))dx+(1/(2n+3)) ∫_0 ^1 (x^(2n+3) /(1+x^2 )) dx...be continued...](Q97722.png) | ||
| ||