Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 97683 by Don08q last updated on 09/Jun/20

$$\mathrm{Evaluate}{\int }_0^1\frac{1}{\sqrt{16+9x^2}}dx$$

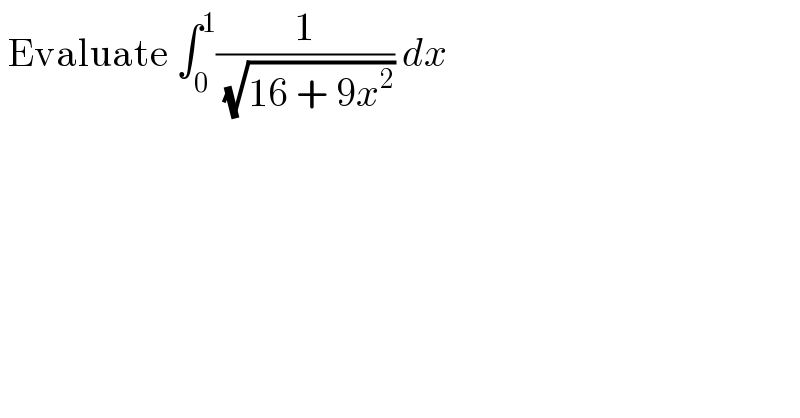
Commented by bemath last updated on 09/Jun/20

$$\mathrm{set}3\mathrm{x}=4\tan \mathrm{z}\Rightarrow 3\mathrm{dx}=4\sec {}^2\mathrm{zdz}$$$$\mathrm{I}=\int \frac{\frac{4}{3}\sec {}^2\mathrm{z}\mathrm{dz}}{\sqrt{16+16\tan {}^2\mathrm{z}}}$$$$\mathrm{I}=\frac{1}{3}\int \sec \mathrm{z}\mathrm{dz}=\frac{1}{3}\ln \mid \sec \mathrm{z}+\tan \mathrm{z}\mid$$$$\mathrm{I}=\frac{1}{3}{[\ln \mid \frac{\sqrt{16+{9\mathrm{x}}^2}}{4}+\frac{3\mathrm{x}}{4}\mid ]}_0^1$$$$=\frac{1}{3}\ln \left(2\right)$$

Commented by Tony Lin last updated on 09/Jun/20

$$\frac{1}{3}{\int }_0^1\frac{1}{\sqrt{{\left(\frac{4}{3}\right)}^2+x^2}}dx$$$$=\frac{1}{3}{sinh}^{-1}\left(\frac{3x}{4}\right){\mid }_0^1$$$$=\frac{1}{3}{sinh}^{-1}\left(\frac{3}{4}\right)$$

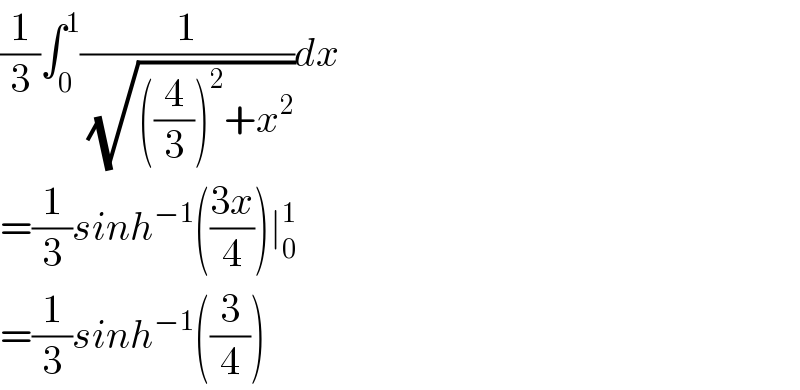
Commented by john santu last updated on 09/Jun/20

$$\mathrm{joosss}\mathrm{coolll}$$

Answered by smridha last updated on 10/Jun/20

$$\frac{1}{3}{\int }_0^1\frac{\mathit{d}\mathit{x}}{\sqrt{{\left(\frac{4}{3}\right)}^2+{\mathit{x}}^2}}=\frac{1}{3}{\left(\mathit{l}\mathit{n}[\mathit{x}+\sqrt{{\left(\frac{4}{3}\right)}^2+{\mathit{x}}^2}]\right)}_0^1$$$$=\frac{1}{3}\mathit{l}\mathit{n}2$$

Answered by Rio Michael last updated on 09/Jun/20

$$\mathcal{R}\mathrm{eca}\mathcal{L}l\int \frac{1}{\sqrt{x^2+a^2}}dx=\ln (x+\sqrt{x^2+a^2})+c$$$$\underset{0}{\stackrel{1}{\int }}\frac{1}{\sqrt{16+9x^2}}dx=\frac{1}{3}\underset{0}{\stackrel{1}{\int }}\frac{1}{\sqrt{x^2+{\left(\frac{4}{3}\right)}^2}}dx=\frac{1}{3}{\left[\ln (x+\sqrt{x^2+{\left(\frac{4}{3}\right)}^2})\right]}_0^1$$$$=\frac{1}{3}[\ln \left(\frac{8}{5}\right)-\ln \left(\frac{4}{3}\right)]=\frac{1}{3}\ln 2$$

Commented by peter frank last updated on 09/Jun/20

$$\mathrm{good}$$

Answered by mathmax by abdo last updated on 09/Jun/20

$$\mathrm{I}={\int }_0^1\frac{\mathrm{dx}}{\sqrt{16+{9\mathrm{x}}^2}}\Rightarrow \mathrm{I}=\frac{1}{4}{\int }_0^1\frac{\mathrm{dx}}{\sqrt{1+\frac{9}{16}{\mathrm{x}}^2}}\mathrm{changement}\frac{3}{4}\mathrm{x}=\mathrm{t}\mathrm{give}$$$$\mathrm{I}=\frac{1}{4}\times {\int }_0^{\frac{3}{4}}\frac{1}{\sqrt{1+{\mathrm{t}}^2}}\times \frac{4}{3}\mathrm{dt}=\frac{1}{3}[\ln {(\mathrm{t}+\sqrt{1+{\mathrm{t}}^2}]}_0^{\frac{3}{4}}=\frac{1}{3}\{\ln (\frac{3}{4}+\sqrt{1+\frac{9}{16}})$$$$=\frac{1}{3}\ln (\frac{3}{4}+\frac{5}{4})=\frac{1}{3}\ln \left(2\right)$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com