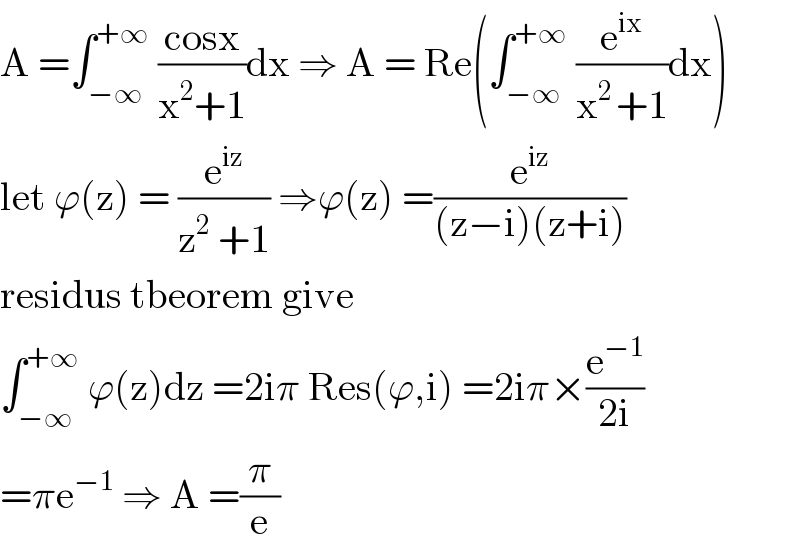Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 97707 by Power last updated on 09/Jun/20

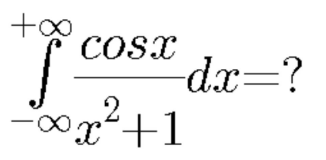
	Answered by smridha last updated on 09/Jun/20

	$= \frac{1}{2} \int_{- \infty}^{+ \infty} \frac{e^{i x}}{x^{2} + 1^{2}} d x + \frac{1}{2} \int_{+ \infty}^{- \infty} \frac{e^{- (- i x)}}{{(- x)}^{2} + 1^{2}} d (- x)$ $= \int_{- \infty}^{+ \infty} \frac{e^{i x}}{x^{2} + 1^{2}} d x = \oint_{C} \frac{e^{i z}}{z^{2} + 1^{2}} d z$ $= \oint_{C} \frac{e^{i z}}{(z + i) (z - i)} d z$ $n o w t i m e f o r c a l c u l a t e t h e r e s i d u e s$ $r e s i d u e a t z_{1} = i$ $\lim_{z \to i} \frac{(z - i) e^{i z}}{(z - i) (z + i)} = \frac{e^{- 1}}{2 i}$ $b u t z_{2} = - i t h i s p o l e d o e s n o t e n c l o s e d$ $b y t h e c a n t o u r (C)$ $n o w :$ $I = \oint_{C} f (z) d z = 2 π i Σ e n c l o s e d r e s u d u e b y t h e c a n t o u r$ $= 2 π i . \frac{e^{- 1}}{2 i} = π e^{- 1}$
	Answered by smridha last updated on 09/Jun/20

	$M e t h o d (2)$ $l e t F (t) = 2 \int_{0}^{+ \infty} \frac{c o s (t x)}{x^{2} + 1} d x [g i v e n i n t e g r a n d i s e v e n]$ $n o w b y L a p l a c e T r a n s f o r m a t i o n$ $f (s) = L [f (t)] . . . . . (i)$ $s o f (s) = \int_{0}^{\infty} e^{- s t} [2 \int_{0}^{\infty} \frac{c o s (t x)}{x^{2} + 1} d x] d t$ $= 2 \int_{0}^{\infty} \frac{1}{x^{2} + 1} [\int_{0}^{\infty} e^{- s t} c o s (t x) d t] d x$ $= 2 \int_{0}^{\infty} \frac{s}{(x^{2} + 1) (s^{2} + x^{2})} d x$ $= \frac{2 s}{(s^{2} - 1)} [\int_{0}^{\infty} (\frac{1}{(x^{2} + 1)} - \frac{1}{(s^{2} + x^{2})}) d x]$ $= \frac{2 s}{(s^{2} - 1)} {[\tan^{- 1} (x) - \frac{1}{s} \tan^{- 1} (\frac{x}{s})]}_{0}^{\infty}$ $= \frac{π}{(s - (- 1))}$ $n o w f r o m (i) F (t) = L^{- 1} [f (s)]$ $= π . L^{- 1} [\frac{1}{(s - (- 1))}]$ $= π e^{- 1}$ $n o w I = F (1) = \frac{π}{e}$
	Commented by Power last updated on 09/Jun/20

	$thanks sir$
	Commented by smridha last updated on 09/Jun/20

	$a l s o t h a n k f u l b e c a u s e t h i s i s$ $v e r y s i g n i f i c a n t i n t e g r a l .$
	Answered by abdomathmax last updated on 09/Jun/20

	$A = \int_{- \infty}^{+ \infty} \frac{cosx}{x^{2} + 1} dx \Rightarrow A = Re (\int_{- \infty}^{+ \infty} \frac{e^{ix}}{x^{2} + 1} dx)$ $let φ (z) = \frac{e^{iz}}{z^{2} + 1} \Rightarrow φ (z) = \frac{e^{iz}}{(z - i) (z + i)}$ $residus tbeorem give$ $\int_{- \infty}^{+ \infty} φ (z) dz = 2 i π Res (φ, i) = 2 i π \times \frac{e^{- 1}}{2 i}$ $= π e^{- 1} \Rightarrow A = \frac{π}{e}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum