Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 97751 by bobhans last updated on 09/Jun/20

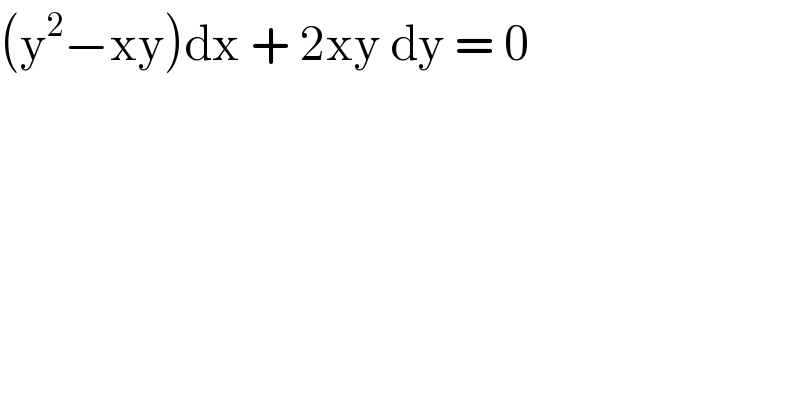
(y^2 −xy)dx + 2xy dy = 0

$$\left(\mathrm{y}^{\mathrm{2}} −\mathrm{xy}\right)\mathrm{dx}\:+\:\mathrm{2xy}\:\mathrm{dy}\:=\:\mathrm{0}\: \\ $$

Commented by bemath last updated on 09/Jun/20

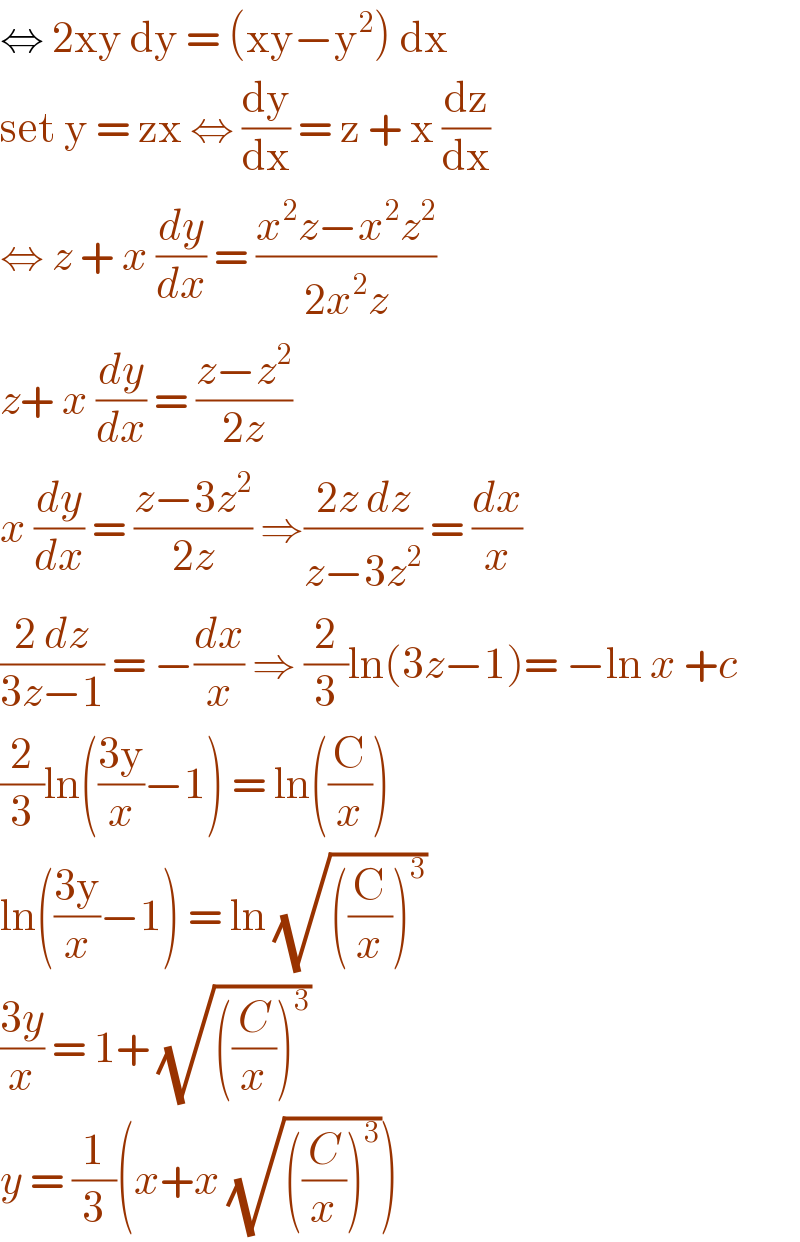
⇔ 2xy dy = (xy−y^2 ) dx set y = zx ⇔ (dy/dx) = z + x (dz/dx) ⇔ z + x (dy/dx) = ((x^2 z−x^2 z^2 )/(2x^2 z)) z+ x (dy/dx) = ((z−z^2 )/(2z)) x (dy/dx) = ((z−3z^2 )/(2z)) ⇒((2z dz)/(z−3z^2 )) = (dx/x) ((2 dz)/(3z−1)) = −(dx/x) ⇒ (2/3)ln(3z−1)= −ln x +c (2/3)ln(((3y)/x)−1) = ln((C/x)) ln(((3y)/x)−1) = ln (√(((C/x))^3 )) ((3y)/x) = 1+ (√(((C/x))^3 )) y = (1/3)(x+x (√(((C/x))^3 )))

$$\Leftrightarrow\:\mathrm{2xy}\:\mathrm{dy}\:=\:\left(\mathrm{xy}−\mathrm{y}^{\mathrm{2}} \right)\:\mathrm{dx}\: \\ $$$$\mathrm{set}\:\mathrm{y}\:=\:\mathrm{zx}\:\Leftrightarrow\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{z}\:+\:\mathrm{x}\:\frac{\mathrm{dz}}{\mathrm{dx}} \\ $$$$\Leftrightarrow\:{z}\:+\:{x}\:\frac{{dy}}{{dx}}\:=\:\frac{{x}^{\mathrm{2}} {z}−{x}^{\mathrm{2}} {z}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} {z}} \\ $$$${z}+\:{x}\:\frac{{dy}}{{dx}}\:=\:\frac{{z}−{z}^{\mathrm{2}} }{\mathrm{2}{z}}\: \\ $$$${x}\:\frac{{dy}}{{dx}}\:=\:\frac{{z}−\mathrm{3}{z}^{\mathrm{2}} }{\mathrm{2}{z}}\:\Rightarrow\frac{\mathrm{2}{z}\:{dz}}{{z}−\mathrm{3}{z}^{\mathrm{2}} }\:=\:\frac{{dx}}{{x}} \\ $$$$\frac{\mathrm{2}\:{dz}}{\mathrm{3}{z}−\mathrm{1}}\:=\:−\frac{{dx}}{{x}}\:\Rightarrow\:\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{3}{z}−\mathrm{1}\right)=\:−\mathrm{ln}\:{x}\:+{c} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\left(\frac{\mathrm{3y}}{{x}}−\mathrm{1}\right)\:=\:\mathrm{ln}\left(\frac{\mathrm{C}}{{x}}\right) \\ $$$$\mathrm{ln}\left(\frac{\mathrm{3y}}{{x}}−\mathrm{1}\right)\:=\:\mathrm{ln}\:\sqrt{\left(\frac{\mathrm{C}}{{x}}\right)^{\mathrm{3}} } \\ $$$$\frac{\mathrm{3}{y}}{{x}}\:=\:\mathrm{1}+\:\sqrt{\left(\frac{{C}}{{x}}\right)^{\mathrm{3}} } \\ $$$${y}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left({x}+{x}\:\sqrt{\left(\frac{{C}}{{x}}\right)^{\mathrm{3}} }\right)\: \\ $$

Commented by bobhans last updated on 09/Jun/20

waw.......

$$\mathrm{waw}....... \\ $$

Commented by john santu last updated on 10/Jun/20

yes..correct

$$\mathrm{yes}..\mathrm{correct}\: \\ $$

Answered by smridha last updated on 09/Jun/20

(∂/∂y)(y^2 −xy)=2y−x≠(∂/∂x)(2xy)=2y this is not exact differential so, (1/(2xy))[2y−x−2y]=−(1/(2y)) I.F=e^(∫−(dy/(2y))) =(1/(√y)) multi:by this of both sides of given eq^n (y^(3/2) −xy^(1/2) )dx+2xy^(1/2) dy=0 now ∫_((keeping y as constant)) (y^(3/2) −xy^(1/2) )dx =xy^(3/2) −(x^2 /2)y^(1/2) and ∫_((terms are donot containing x)) (0)dy=0 so solution: xy^(3/2) −(x^2 /2)y^(1/2) =c

$$\frac{\partial}{\partial{y}}\left(\boldsymbol{{y}}^{\mathrm{2}} −\boldsymbol{{xy}}\right)=\mathrm{2}\boldsymbol{{y}}−\boldsymbol{{x}}\neq\frac{\partial}{\partial\boldsymbol{{x}}}\left(\mathrm{2}\boldsymbol{{xy}}\right)=\mathrm{2}\boldsymbol{{y}} \\ $$$$\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{not}}\:\boldsymbol{{exact}}\:\boldsymbol{{differential}} \\ $$$$\boldsymbol{{so}},\:\frac{\mathrm{1}}{\mathrm{2}{xy}}\left[\mathrm{2}{y}−\boldsymbol{{x}}−\mathrm{2}\boldsymbol{{y}}\right]=−\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{y}}} \\ $$$$\boldsymbol{{I}}.{F}={e}^{\int−\frac{{dy}}{\mathrm{2}\boldsymbol{{y}}}} =\frac{\mathrm{1}}{\sqrt{\boldsymbol{{y}}}}\:\:\:\boldsymbol{{multi}}:\boldsymbol{{by}}\:\boldsymbol{{this}}\:\boldsymbol{{of}}\:\boldsymbol{{both}} \\ $$$$\boldsymbol{{sides}}\:\boldsymbol{{of}}\:\boldsymbol{{given}}\:\boldsymbol{{eq}}^{\boldsymbol{{n}}} \\ $$$$\left(\boldsymbol{{y}}^{\frac{\mathrm{3}}{\mathrm{2}}} −\boldsymbol{{xy}}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)\boldsymbol{{dx}}+\mathrm{2}\boldsymbol{{xy}}^{\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{{dy}}=\mathrm{0} \\ $$$$\boldsymbol{{now}}\:\int_{\left({keeping}\:\boldsymbol{{y}}\:\boldsymbol{{as}}\:\boldsymbol{{constant}}\right)} \left(\boldsymbol{{y}}^{\frac{\mathrm{3}}{\mathrm{2}}} −\boldsymbol{{xy}}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)\boldsymbol{{dx}} \\ $$$$=\boldsymbol{{xy}}^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{2}}\boldsymbol{{y}}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\boldsymbol{{and}}\:\int_{\left(\boldsymbol{{terms}}\:\boldsymbol{{are}}\:\boldsymbol{{donot}}\:\boldsymbol{{containing}}\:\boldsymbol{{x}}\right)} \left(\mathrm{0}\right)\boldsymbol{{dy}}=\mathrm{0} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{solution}}: \\ $$$$\:\:\:\:{x}\boldsymbol{{y}}^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{2}}\boldsymbol{{y}}^{\frac{\mathrm{1}}{\mathrm{2}}} =\boldsymbol{{c}} \\ $$

Commented by mr W last updated on 09/Jun/20

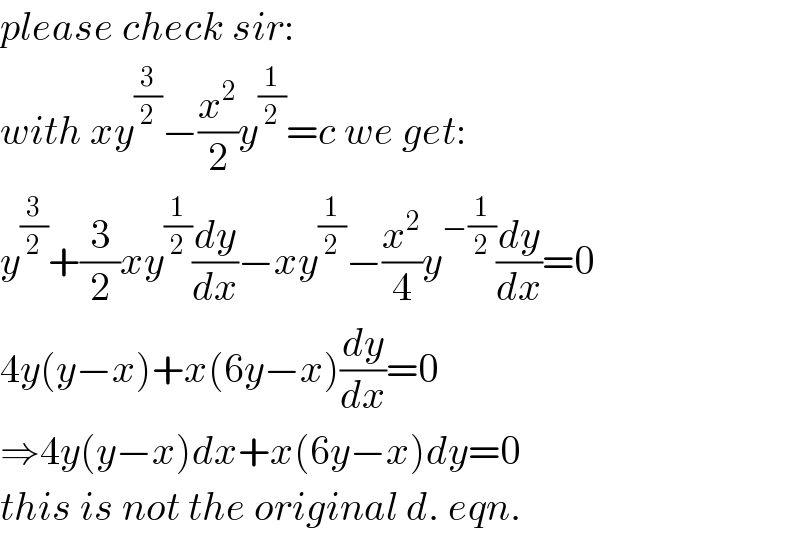
please check sir: with xy^(3/2) −(x^2 /2)y^(1/2) =c we get: y^(3/2) +(3/2)xy^(1/2) (dy/dx)−xy^(1/2) −(x^2 /4)y^(−(1/2)) (dy/dx)=0 4y(y−x)+x(6y−x)(dy/dx)=0 ⇒4y(y−x)dx+x(6y−x)dy=0 this is not the original d. eqn.

$${please}\:{check}\:{sir}: \\ $$$${with}\:{xy}^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{y}^{\frac{\mathrm{1}}{\mathrm{2}}} ={c}\:{we}\:{get}: \\ $$$${y}^{\frac{\mathrm{3}}{\mathrm{2}}} +\frac{\mathrm{3}}{\mathrm{2}}{xy}^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{dy}}{{dx}}−{xy}^{\frac{\mathrm{1}}{\mathrm{2}}} −\frac{{x}^{\mathrm{2}} }{\mathrm{4}}{y}^{−\frac{\mathrm{1}}{\mathrm{2}}} \frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\mathrm{4}{y}\left({y}−{x}\right)+{x}\left(\mathrm{6}{y}−{x}\right)\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}{y}\left({y}−{x}\right){dx}+{x}\left(\mathrm{6}{y}−{x}\right){dy}=\mathrm{0} \\ $$$${this}\:{is}\:{not}\:{the}\:{original}\:{d}.\:{eqn}. \\ $$

Commented by smridha last updated on 09/Jun/20

I donot find any mistake.. if you can then show me....

$$\boldsymbol{{I}}\:{do}\boldsymbol{{not}}\:\boldsymbol{{find}}\:\boldsymbol{{any}}\:\boldsymbol{{mistake}}.. \\ $$$$\boldsymbol{{if}}\:\boldsymbol{{you}}\:\boldsymbol{{can}}\:\boldsymbol{{then}}\:\boldsymbol{{show}}\:\boldsymbol{{me}}.... \\ $$

Commented by prakash jain last updated on 10/Jun/20

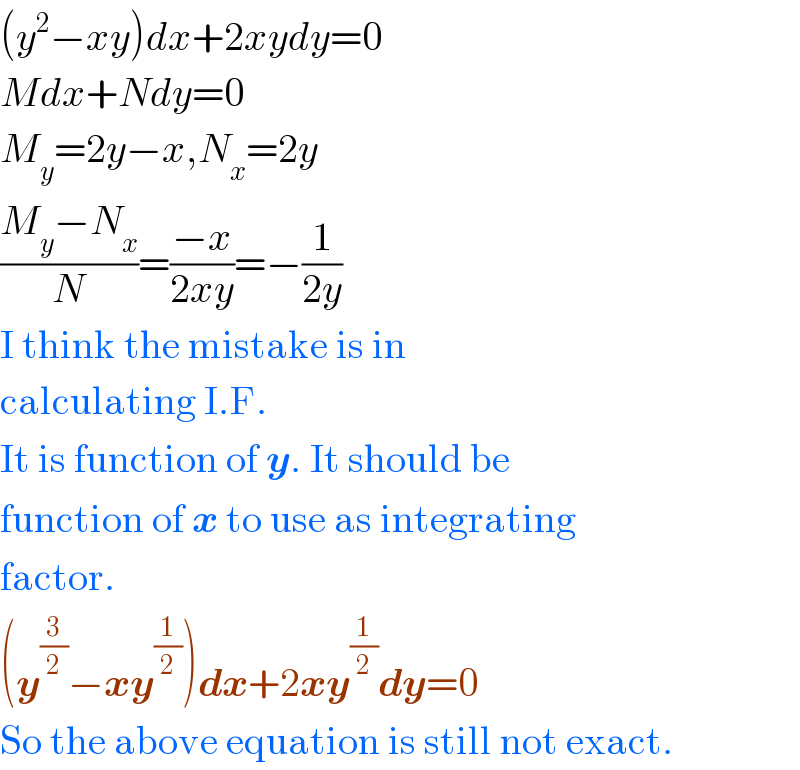
(y^2 −xy)dx+2xydy=0 Mdx+Ndy=0 M_y =2y−x,N_x =2y ((M_y −N_x )/N)=((−x)/(2xy))=−(1/(2y)) I think the mistake is in calculating I.F. It is function of y. It should be function of x to use as integrating factor. (y^(3/2) −xy^(1/2) )dx+2xy^(1/2) dy=0 So the above equation is still not exact.

$$\left({y}^{\mathrm{2}} −{xy}\right){dx}+\mathrm{2}{xydy}=\mathrm{0} \\ $$$${Mdx}+{Ndy}=\mathrm{0} \\ $$$${M}_{{y}} =\mathrm{2}{y}−{x},{N}_{{x}} =\mathrm{2}{y} \\ $$$$\frac{{M}_{{y}} −{N}_{{x}} }{{N}}=\frac{−{x}}{\mathrm{2}{xy}}=−\frac{\mathrm{1}}{\mathrm{2}{y}} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{mistake}\:\mathrm{is}\:\mathrm{in} \\ $$$$\mathrm{calculating}\:\mathrm{I}.\mathrm{F}. \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{function}\:\mathrm{of}\:\boldsymbol{{y}}.\:\mathrm{It}\:\mathrm{should}\:\mathrm{be} \\ $$$$\mathrm{function}\:\mathrm{of}\:\boldsymbol{{x}}\:\mathrm{to}\:\mathrm{use}\:\mathrm{as}\:\mathrm{integrating} \\ $$$$\mathrm{factor}. \\ $$$$\left(\boldsymbol{{y}}^{\frac{\mathrm{3}}{\mathrm{2}}} −\boldsymbol{{xy}}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)\boldsymbol{{dx}}+\mathrm{2}\boldsymbol{{xy}}^{\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{{dy}}=\mathrm{0} \\ $$$$\mathrm{So}\:\mathrm{the}\:\mathrm{above}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{still}\:\mathrm{not}\:\mathrm{exact}. \\ $$

Commented by smridha last updated on 10/Jun/20

yeah my second solution tells the truth ....but i am not yet understand why the IF is different for this two mehods.....two method sshould be analogus to each other....

$${ye}\boldsymbol{{ah}}\:\boldsymbol{{my}}\:\boldsymbol{{second}}\:\boldsymbol{{solution}}\:\boldsymbol{{tells}} \\ $$$$\boldsymbol{{th}}{e}\:\boldsymbol{{truth}}\:....\boldsymbol{{but}}\:\boldsymbol{{i}}\:\boldsymbol{{am}}\:\boldsymbol{{not}}\:\boldsymbol{{yet}} \\ $$$$\boldsymbol{{understand}}\:\boldsymbol{{why}}\:\boldsymbol{{the}}\:\boldsymbol{{I}}{F}\:\boldsymbol{{is}}\:\boldsymbol{{different}} \\ $$$$\boldsymbol{{for}}\:\boldsymbol{{this}}\:\boldsymbol{{two}}\:\boldsymbol{{mehods}}.....\boldsymbol{{two}} \\ $$$$\boldsymbol{{method}}\:{s}\boldsymbol{{should}}\:\boldsymbol{{be}}\:\boldsymbol{{analogus}} \\ $$$$\boldsymbol{{t}}{o}\:\boldsymbol{{each}}\:\boldsymbol{{other}}.... \\ $$$$ \\ $$

Commented by prakash jain last updated on 10/Jun/20

((M_y −N_x )/N) should not have y and should be a fuction of only x. So there is a mistake in method used for computing I.F in the answer above

$$\frac{{M}_{{y}} −{N}_{{x}} }{{N}}\:\mathrm{should}\:\mathrm{not}\:\mathrm{have}\:{y}\:\mathrm{and} \\ $$$$\mathrm{should}\:\mathrm{be}\:\mathrm{a}\:\mathrm{fuction}\:\mathrm{of}\:\mathrm{only}\:{x}. \\ $$$$\mathrm{So}\:\mathrm{there}\:\mathrm{is}\:\mathrm{a}\:\mathrm{mistake}\:\mathrm{in}\:\mathrm{method}\: \\ $$$$\mathrm{used}\:\mathrm{for}\:\mathrm{computing}\:\mathrm{I}.\mathrm{F}\:\mathrm{in}\:\mathrm{the}\:\mathrm{answer} \\ $$$$\mathrm{above} \\ $$

Answered by smridha last updated on 10/Jun/20

(y^2 −xy)dx+2xydy=0 (dy/dx)+(y/(2x))=(1/2) so IF=e^(∫(dx/(2x))) =(√x) mult: and integrating by both sides with this we get ∫d(y(√x))=(1/2)∫(√x)dx so the solution is y(√x)=(1/3)x^(3/2) +c now this is perfect....but still I have confution why my previous method didnot work...probably I did silly mistake anywhere....

$$\left(\boldsymbol{{y}}^{\mathrm{2}} −\boldsymbol{{xy}}\right)\boldsymbol{{dx}}+\mathrm{2}\boldsymbol{{xydy}}=\mathrm{0} \\ $$$$\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}+\frac{\boldsymbol{{y}}}{\mathrm{2}\boldsymbol{{x}}}=\frac{\mathrm{1}}{\mathrm{2}}\:\boldsymbol{{so}}\:\boldsymbol{{IF}}=\boldsymbol{{e}}^{\int\frac{\boldsymbol{{dx}}}{\mathrm{2}\boldsymbol{{x}}}} =\sqrt{\boldsymbol{{x}}} \\ $$$$\boldsymbol{{mult}}:\:\:\boldsymbol{{and}}\:\boldsymbol{{integrating}}\:\boldsymbol{{by}}\:\boldsymbol{{both}}\:\boldsymbol{{sides}}\:\boldsymbol{{with}}\:\boldsymbol{{this}}\:\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$\int\boldsymbol{{d}}\left(\boldsymbol{{y}}\sqrt{\boldsymbol{{x}}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{{x}}{dx} \\ $$$${so}\:{the}\:\boldsymbol{{solution}}\:\boldsymbol{{is}} \\ $$$$\boldsymbol{{y}}\sqrt{\boldsymbol{{x}}}=\frac{\mathrm{1}}{\mathrm{3}}\boldsymbol{{x}}^{\frac{\mathrm{3}}{\mathrm{2}}} +\boldsymbol{{c}} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{perfect}}....\boldsymbol{{but}}\:\boldsymbol{{still}}\:\boldsymbol{{I}} \\ $$$$\boldsymbol{{have}}\:\boldsymbol{{confution}}\:\boldsymbol{{why}}\:\boldsymbol{{my}}\:\boldsymbol{{previous}} \\ $$$$\boldsymbol{{method}}\:\boldsymbol{{didnot}}\:\boldsymbol{{work}}...\boldsymbol{{probably}} \\ $$$$\boldsymbol{{I}}\:\boldsymbol{{did}}\:\boldsymbol{{silly}}\:\boldsymbol{{mistake}}\:\boldsymbol{{anywhere}}.... \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com