
Question and Answers Forum
Question Number 97823 by john santu last updated on 10/Jun/20

Commented by bobhans last updated on 10/Jun/20
![let x is an integer. we can write x^3 −7x = x(x^2 −7) if x is divisible by 3 , then we′re done. otherwise ,x must have remainder 1 or 2 in the divisibility by 3. thus x^2 must has remainder 1 (3k+1)^2 = 3[ k(3k+2)] +1 , k∈Z](Q97830.png)
Commented by john santu last updated on 10/Jun/20

Answered by Rio Michael last updated on 10/Jun/20
![let f(x) = x^3 −7x ⇒ f(x + 1) = (x + 1)^3 −7(x + 1) −[x^3 −7x] f(x + 1)−f(x) = x^3 + 3x^(2 ) + 3x + 1−7x−7 −x^3 + 7x = 3x^2 + 3x −6 = 3(x^2 + x −2) , (x^2 + x −2) ∈ Z by mathematical induction.](Q97824.png)
Answered by MJS last updated on 10/Jun/20
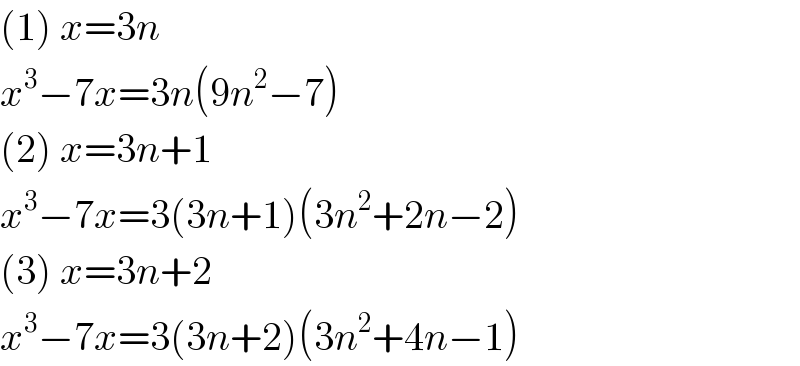
Answered by floor(10²Eta[1]) last updated on 10/Jun/20

Answered by 1549442205 last updated on 10/Jun/20
![x^3 −7x=[(x−1)x(x+1)−6x]⋮3 since (x−1)x(x+1)⋮3(among three consecutive always have at least one number divide by 3) and 6x⋮3](Q97904.png)
