Question Number 97839 by mathmax by abdo last updated on 10/Jun/20
$$\mathrm{calculate}\:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\frac{\mathrm{n}\pi}{\mathrm{4}}} \:\frac{\mathrm{dx}}{\mathrm{3cos}^{\mathrm{4}} \mathrm{x}\:+\mathrm{3sin}^{\mathrm{4}} \mathrm{x}−\mathrm{1}} \\ $$
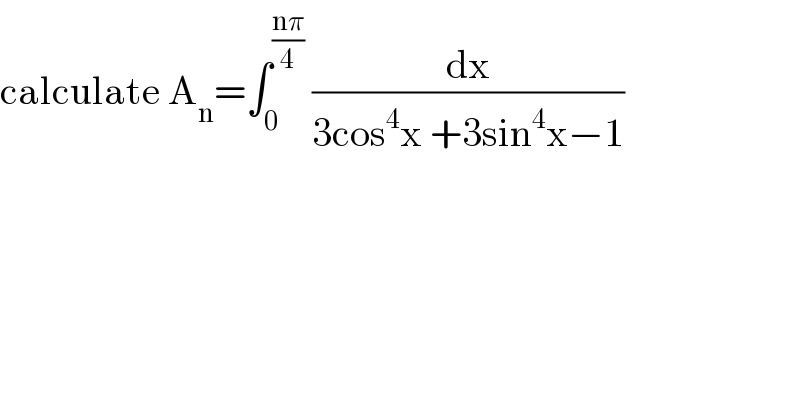
Commented by mr W last updated on 10/Jun/20
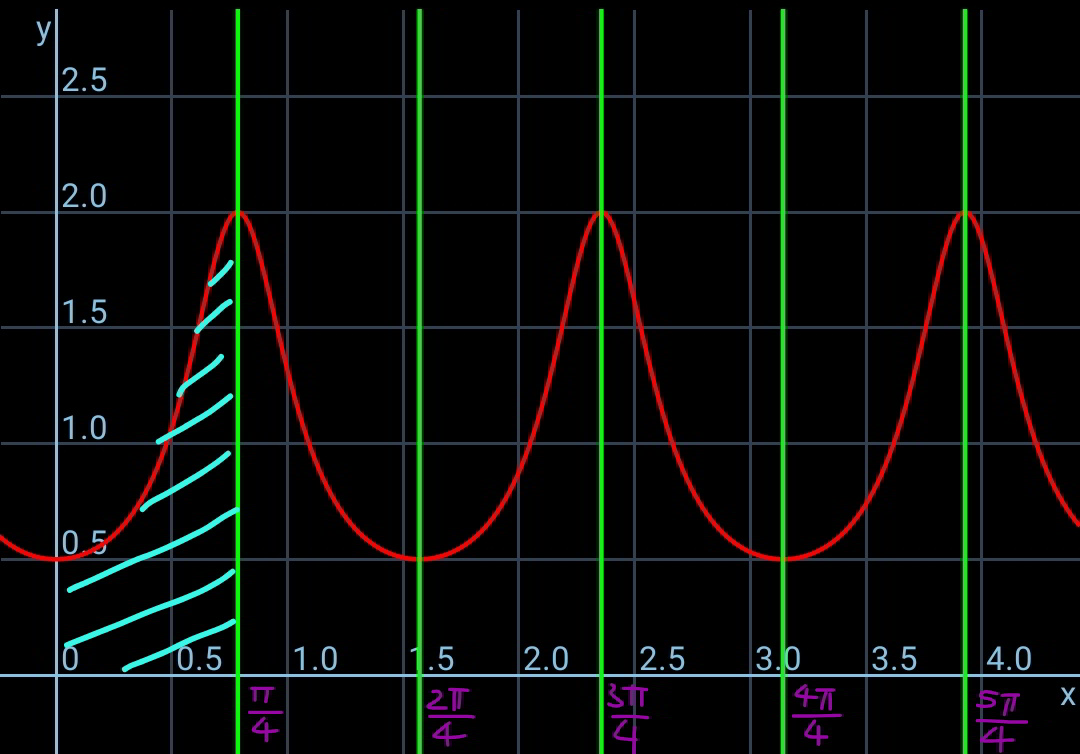
![3(cos^4 x+sin^4 x)−1 =3(cos^4 x+sin^4 x+2 cos^2 x sin^2 x)−1−(3/2) sin^2 2x =3(cos^2 x+sin^2 x)^2 −1−(3/2) sin^2 2x =(1/2)(4−3 sin^2 2x)≤2, ≥(1/2) ⇒(1/2)≤(1/(3cos^4 x+3 sin^4 x−1))≤2 ⇒∫_0 ^((nπ)/4) (dx/(3cos^4 x+3 sin^4 x−1))>(1/2)×((nπ)/4)=((nπ)/8) ⇒∫_0 ^((nπ)/4) (dx/(3cos^4 x+3 sin^4 x−1))<2×((nπ)/4)=((nπ)/2) ⇒((nπ)/8)<A_n <((nπ)/2) i.e. A_n is always >0, can never be zero! A_n =∫_0 ^((nπ)/4) ((2dx)/(4−3 sin^2 2x)) =∫_0 ^((nπ)/2) (dt/(4−3 sin^2 t)) with t=2x =n∫_0 ^(π/2) (dt/(4−3 sin^2 t)) =n[(1/2)tan^(−1) ((tan t)/2)]_0 ^(π/2) =(n/2)×(π/2) =((nπ)/4)](Q97851.png)
$$\mathrm{3}\left(\mathrm{cos}^{\mathrm{4}} \:{x}+\mathrm{sin}^{\mathrm{4}} \:{x}\right)−\mathrm{1} \\ $$$$=\mathrm{3}\left(\mathrm{cos}^{\mathrm{4}} \:{x}+\mathrm{sin}^{\mathrm{4}} \:{x}+\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:{x}\:\mathrm{sin}^{\mathrm{2}} \:{x}\right)−\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x} \\ $$$$=\mathrm{3}\left(\mathrm{cos}^{\mathrm{2}} \:{x}+\mathrm{sin}^{\mathrm{2}} \:{x}\right)^{\mathrm{2}} −\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4}−\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}\right)\leqslant\mathrm{2},\:\geqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\leqslant\frac{\mathrm{1}}{\mathrm{3cos}^{\mathrm{4}} \:{x}+\mathrm{3}\:\mathrm{sin}^{\mathrm{4}} \:{x}−\mathrm{1}}\leqslant\mathrm{2} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\frac{{n}\pi}{\mathrm{4}}} \frac{{dx}}{\mathrm{3cos}^{\mathrm{4}} \:{x}+\mathrm{3}\:\mathrm{sin}^{\mathrm{4}} \:{x}−\mathrm{1}}>\frac{\mathrm{1}}{\mathrm{2}}×\frac{{n}\pi}{\mathrm{4}}=\frac{{n}\pi}{\mathrm{8}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\frac{{n}\pi}{\mathrm{4}}} \frac{{dx}}{\mathrm{3cos}^{\mathrm{4}} \:{x}+\mathrm{3}\:\mathrm{sin}^{\mathrm{4}} \:{x}−\mathrm{1}}<\mathrm{2}×\frac{{n}\pi}{\mathrm{4}}=\frac{{n}\pi}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{n}\pi}{\mathrm{8}}<{A}_{{n}} <\frac{{n}\pi}{\mathrm{2}} \\ $$$${i}.{e}.\:{A}_{{n}} \:{is}\:{always}\:>\mathrm{0},\:{can}\:{never}\:{be}\:{zero}! \\ $$$$ \\ $$$${A}_{{n}} =\int_{\mathrm{0}} ^{\frac{{n}\pi}{\mathrm{4}}} \frac{\mathrm{2}{dx}}{\mathrm{4}−\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{{n}\pi}{\mathrm{2}}} \frac{{dt}}{\mathrm{4}−\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:{t}}\:\:{with}\:{t}=\mathrm{2}{x} \\ $$$$={n}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dt}}{\mathrm{4}−\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:{t}} \\ $$$$={n}\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{tan}\:{t}}{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{{n}}{\mathrm{2}}×\frac{\pi}{\mathrm{2}} \\ $$$$=\frac{{n}\pi}{\mathrm{4}} \\ $$
Answered by smridha last updated on 10/Jun/20
$$\boldsymbol{{for}}\:\boldsymbol{{n}}\:\boldsymbol{{odd}}\:\boldsymbol{{A}}_{\boldsymbol{{n}}} =\frac{\boldsymbol{\pi}}{\mathrm{4}} \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{for}}\:\boldsymbol{{even}}\:\boldsymbol{{n}}\:\boldsymbol{{A}}_{\boldsymbol{{n}}} =\mathrm{0} \\ $$
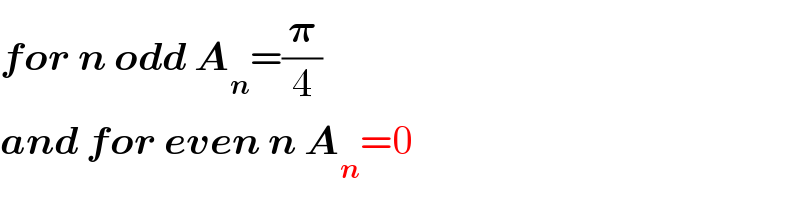
Answered by smridha last updated on 10/Jun/20
![∫_0 ^((n𝛑)/4) ((d(tan(2x)))/(2^2 +(tan(2x))^2 ))=(1/2)(tan^(−1) [((tan(2x))/2)])_0 ^((n𝛑)/4) =(1/2)(tan^(−1) [((tan(((n𝛑)/2)))/2)]) now for n=2m (even) A_n =0 n=2m+1(odd) A_n =(π/4)](Q97853.png)
$$\int_{\mathrm{0}} ^{\frac{\boldsymbol{{n}\pi}}{\mathrm{4}}} \frac{\boldsymbol{{d}}\left(\boldsymbol{{tan}}\left(\mathrm{2}\boldsymbol{{x}}\right)\right)}{\mathrm{2}^{\mathrm{2}} +\left(\boldsymbol{{tan}}\left(\mathrm{2}\boldsymbol{{x}}\right)\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{tan}^{−\mathrm{1}} \left[\frac{\boldsymbol{{tan}}\left(\mathrm{2}\boldsymbol{{x}}\right)}{\mathrm{2}}\right]\right)_{\mathrm{0}} ^{\frac{\boldsymbol{{n}\pi}}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{tan}^{−\mathrm{1}} \left[\frac{\boldsymbol{{tan}}\left(\frac{\boldsymbol{{n}\pi}}{\mathrm{2}}\right)}{\mathrm{2}}\right]\right) \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{for}}\:\boldsymbol{{n}}=\mathrm{2}\boldsymbol{{m}}\:\left(\boldsymbol{{even}}\right)\:{A}_{{n}} =\mathrm{0} \\ $$$$\boldsymbol{{n}}=\mathrm{2}\boldsymbol{{m}}+\mathrm{1}\left(\boldsymbol{{odd}}\right)\:\boldsymbol{{A}}_{{n}} =\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$
Answered by abdomathmax last updated on 10/Jun/20
![we have 3(cos^4 x+sin^4 x)−1 =3{ (cos^2 x +sin^2 x)^2 −2cos^2 x sin^2 x}−1 =3{1−(1/2)sin^2 (2x)}−1 =2−(3/2)×((1−cos(4x))/2) =2−(3/4) +(3/4)cos(4x) =(5/4) +(3/4) cos(4x) ⇒ A_n =4∫_0 ^((nπ)/4) (dx/(5 +3cos(4x))) =_(4x=t) 4 ∫_0 ^(nπ) (dt/(4(5+3cost))) =∫_0 ^(nπ) (dt/(5+3cost)) =_(tan((t/2))=u) ∫_0 ^(tan(((nπ)/2))) ((2du)/((1+u^2 )(5+3((1−u^2 )/(1+u^2 ))))) =2∫_0 ^(tan(((nπ)/2))) (du/(5+5u^2 +3−3u^2 )) =2∫_0 ^(tan(((nπ)/2))) (du/(8+2u^2 )) =∫_0 ^(tan(((nπ)/2))) (du/(4+u^2 )) =_(u=2z) ∫_0 ^((1/2)tan(((nπ)/2))) ((2dz)/(4(1+z^2 ))) =(1/2) [arctan(z)]_0 ^((1/2)tan(((nπ)/2))) =(1/2) arctan((1/2)tan(((nπ)/2))) ⇒ A_(2n) =0 and A_(2n+1) =(1/2)×(π/2) =(π/4)](Q97921.png)
$$\mathrm{we}\:\mathrm{have}\:\mathrm{3}\left(\mathrm{cos}^{\mathrm{4}} \mathrm{x}+\mathrm{sin}^{\mathrm{4}} \mathrm{x}\right)−\mathrm{1} \\ $$$$=\mathrm{3}\left\{\:\left(\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:+\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} −\mathrm{2cos}^{\mathrm{2}} \mathrm{x}\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right\}−\mathrm{1} \\ $$$$=\mathrm{3}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2x}\right)\right\}−\mathrm{1}\:=\mathrm{2}−\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{4x}\right)}{\mathrm{2}} \\ $$$$=\mathrm{2}−\frac{\mathrm{3}}{\mathrm{4}}\:+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{cos}\left(\mathrm{4x}\right)\:=\frac{\mathrm{5}}{\mathrm{4}}\:+\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{cos}\left(\mathrm{4x}\right)\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\mathrm{4}\int_{\mathrm{0}} ^{\frac{\mathrm{n}\pi}{\mathrm{4}}} \:\frac{\mathrm{dx}}{\mathrm{5}\:+\mathrm{3cos}\left(\mathrm{4x}\right)} \\ $$$$=_{\mathrm{4x}=\mathrm{t}} \:\:\:\mathrm{4}\:\int_{\mathrm{0}} ^{\mathrm{n}\pi} \:\frac{\mathrm{dt}}{\mathrm{4}\left(\mathrm{5}+\mathrm{3cost}\right)}\:=\int_{\mathrm{0}} ^{\mathrm{n}\pi} \:\frac{\mathrm{dt}}{\mathrm{5}+\mathrm{3cost}} \\ $$$$=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{u}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{tan}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)} \:\frac{\mathrm{2du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\left(\mathrm{5}+\mathrm{3}\frac{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\right)} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{tan}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)} \:\:\frac{\mathrm{du}}{\mathrm{5}+\mathrm{5u}^{\mathrm{2}} \:+\mathrm{3}−\mathrm{3u}^{\mathrm{2}} }\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{tan}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)} \:\frac{\mathrm{du}}{\mathrm{8}+\mathrm{2u}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{tan}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)} \:\frac{\mathrm{du}}{\mathrm{4}+\mathrm{u}^{\mathrm{2}} }\:=_{\mathrm{u}=\mathrm{2z}} \:\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)} \:\frac{\mathrm{2dz}}{\mathrm{4}\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\:\left[\mathrm{arctan}\left(\mathrm{z}\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\right)\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{2n}} =\mathrm{0}\:\mathrm{and} \\ $$$$\mathrm{A}_{\mathrm{2n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\mathrm{4}} \\ $$
Commented by smridha last updated on 10/Jun/20
$$\boldsymbol{{thanks}}\:\boldsymbol{{a}}\:\boldsymbol{{lot}}\:\boldsymbol{{for}}\:\boldsymbol{{conformation}}. \\ $$
Commented by mr W last updated on 10/Jun/20
$${prof}.\:{abdo}\:{sir}: \\ $$$${the}\:{result}\:{A}_{\mathrm{2}{n}} =\mathrm{0}\:{and}\:{A}_{\mathrm{2}{n}+\mathrm{1}} =\frac{\pi}{\mathrm{4}}\:{is} \\ $$$${definitively}\:{not}\:{correct}.\:{as}\:{i}\:{showed} \\ $$$${above},\:\frac{{n}\pi}{\mathrm{8}}<{A}_{{n}} <\frac{{n}\pi}{\mathrm{2}},\:{this}\:{is}\:{for}\:{sure}. \\ $$$${if}\:{f}\left({x}\right)\geqslant\frac{\mathrm{1}}{\mathrm{2}},\:\int_{{a}} ^{{b}} {f}\left({x}\right){dx}\:{can}\:{never}\:{be}\:\mathrm{0}! \\ $$$${i}\:{think}\:{we}\:{don}'{t}\:{need}\:{to}\:{discuss}\:{this}. \\ $$$$ \\ $$$${the}\:{question}\:{is}\:{where}\:{is}\:{the}\:{mistake} \\ $$$${in}\:{your}\:{working}.\:{i}\:{think}\:{the}\:{mistake} \\ $$$${lies}\:{in}\:{the}\:{use}\:{of}\:{functions}\:\mathrm{tan}\:{x}\:{and} \\ $$$$\mathrm{tan}^{−\mathrm{1}} {x}.\:{we}\:{must}\:{be}\:{very}\:{careful}\:{with} \\ $$$${them},\:{because}\:\mathrm{tan}\:{x}\:{is}\:{not}\:{continuous}. \\ $$$${i}\:{let}\:{you}\:{think}\:{about}\:{that}.\:{you}\:{know} \\ $$$${what}\:{i}\:{mean}. \\ $$$$ \\ $$$${the}\:{correct}\:{way}\:{to}\:{treat}\:{this}\:{problem} \\ $$$${is}\:{to}\:{divide}\:{the}\:{interval}\:{of}\:{integral} \\ $$$$\mathrm{0}\rightarrow\frac{{n}\pi}{\mathrm{4}}\:{into}\:{many}\:{small}\:{segments}, \\ $$$${within}\:{each}\:{of}\:{these}\:{segments}\:{the} \\ $$$${function}\:{is}\:{continuous}.\:{i}.{e}.\:{we}\:{take} \\ $$$$\mathrm{0}\rightarrow\frac{\pi}{\mathrm{4}} \\ $$$$\frac{\pi}{\mathrm{4}}\rightarrow\frac{\mathrm{2}\pi}{\mathrm{4}} \\ $$$$\frac{\mathrm{2}\pi}{\mathrm{4}}\rightarrow\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$$... \\ $$$$\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{4}}\rightarrow\frac{{n}\pi}{\mathrm{4}} \\ $$$${you}\:{will}\:{see}\:{in}\:{each}\:{of}\:{these}\:{segments} \\ $$$${the}\:{integral}\:{delivers}\:{the}\:{result}\:\frac{\pi}{\mathrm{4}}, \\ $$$${therefore}\:{the}\:{total}\:{result}\:{is}\:{n}×\frac{\pi}{\mathrm{4}}. \\ $$$${A}_{{n}} =\int_{\mathrm{0}} ^{\frac{{n}\pi}{\mathrm{4}}} {f}\left({x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {f}\left({x}\right){dx}+\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\mathrm{2}\pi}{\mathrm{4}}} {f}\left({x}\right){dx}+...+\int_{\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{4}}} ^{\frac{{n}\pi}{\mathrm{4}}} {f}\left({x}\right){dx} \\ $$$$=\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{4}}+...+\frac{\pi}{\mathrm{4}} \\ $$$$={n}×\frac{\pi}{\mathrm{4}} \\ $$$$=\frac{{n}\pi}{\mathrm{4}} \\ $$
Commented by mr W last updated on 10/Jun/20
Commented by mathmax by abdo last updated on 10/Jun/20
$$\mathrm{thank}\:\mathrm{sir}\:\mathrm{for}\:\mathrm{this}\:\mathrm{clarification} \\ $$
Commented by mr W last updated on 10/Jun/20
$${thanks}\:{for}\:{the}\:{nice}\:{question}! \\ $$