Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 97866 by me2love2math last updated on 10/Jun/20

Commented by me2love2math last updated on 10/Jun/20

1 2 5 and 6

$$\mathrm{1}\:\mathrm{2}\:\mathrm{5}\:{and}\:\mathrm{6} \\ $$

Commented by bobhans last updated on 10/Jun/20

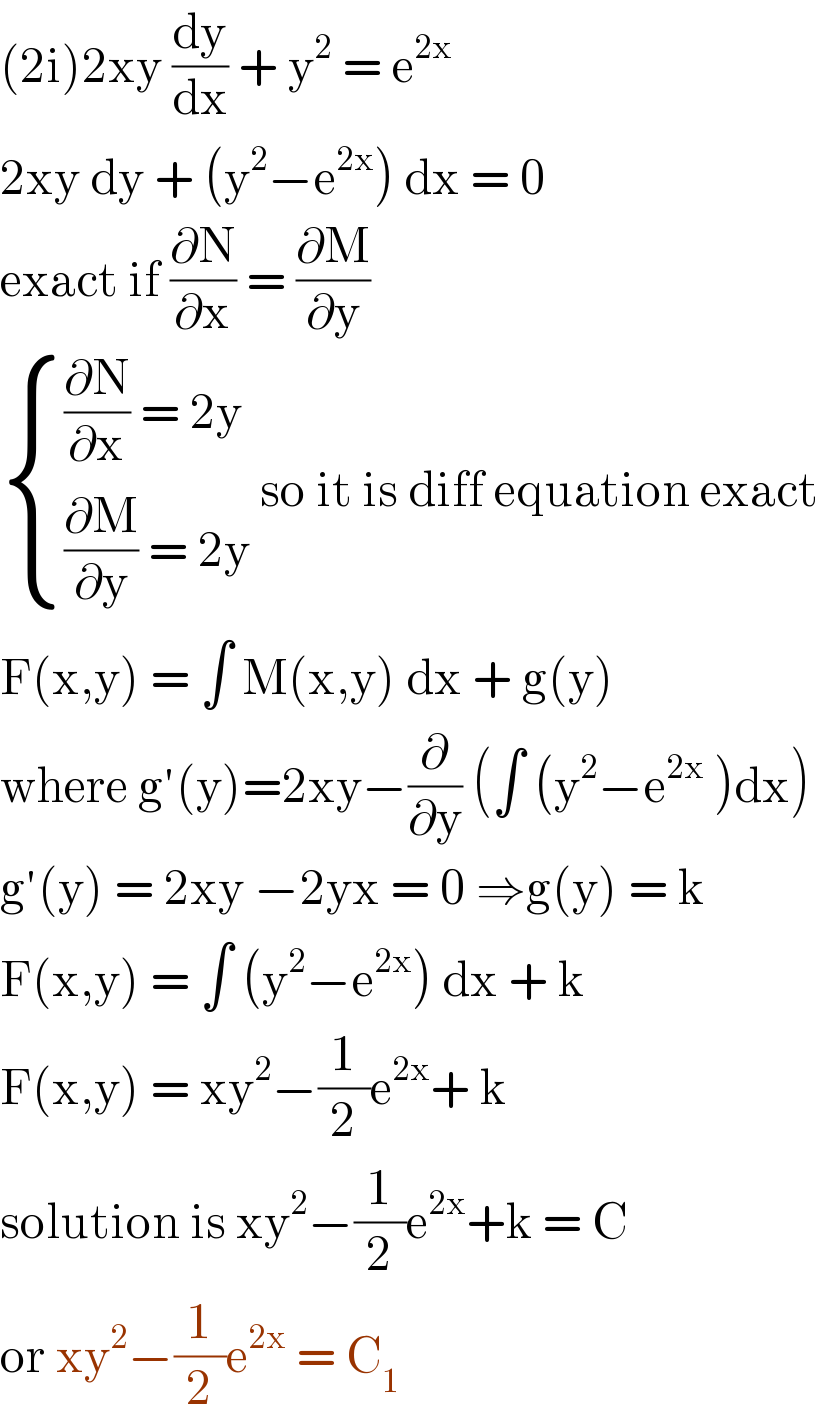
(2i)2xy (dy/dx) + y^2 = e^(2x) 2xy dy + (y^2 −e^(2x) ) dx = 0 exact if (∂N/∂x) = (∂M/∂y) { (((∂N/∂x) = 2y)),(((∂M/∂y) = 2y)) :} so it is diff equation exact F(x,y) = ∫ M(x,y) dx + g(y) where g′(y)=2xy−(∂/∂y) (∫ (y^2 −e^(2x) )dx) g′(y) = 2xy −2yx = 0 ⇒g(y) = k F(x,y) = ∫ (y^2 −e^(2x) ) dx + k F(x,y) = xy^2 −(1/2)e^(2x) + k solution is xy^2 −(1/2)e^(2x) +k = C or xy^2 −(1/2)e^(2x) = C_1

$$\left(\mathrm{2i}\right)\mathrm{2xy}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{e}^{\mathrm{2x}} \\ $$$$\mathrm{2xy}\:\mathrm{dy}\:+\:\left(\mathrm{y}^{\mathrm{2}} −\mathrm{e}^{\mathrm{2x}} \right)\:\mathrm{dx}\:=\:\mathrm{0} \\ $$$$\mathrm{exact}\:\mathrm{if}\:\frac{\partial\mathrm{N}}{\partial\mathrm{x}}\:=\:\frac{\partial\mathrm{M}}{\partial\mathrm{y}} \\ $$$$\begin{cases}{\frac{\partial\mathrm{N}}{\partial\mathrm{x}}\:=\:\mathrm{2y}}\\{\frac{\partial\mathrm{M}}{\partial\mathrm{y}}\:=\:\mathrm{2y}}\end{cases}\:\mathrm{so}\:\mathrm{it}\:\mathrm{is}\:\mathrm{diff}\:\mathrm{equation}\:\mathrm{exact} \\ $$$$\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)\:=\:\int\:\mathrm{M}\left(\mathrm{x},\mathrm{y}\right)\:\mathrm{dx}\:+\:\mathrm{g}\left(\mathrm{y}\right) \\ $$$$\mathrm{where}\:\mathrm{g}'\left(\mathrm{y}\right)=\mathrm{2xy}−\frac{\partial}{\partial\mathrm{y}}\:\left(\int\:\left(\mathrm{y}^{\mathrm{2}} −\mathrm{e}^{\mathrm{2x}} \:\right)\mathrm{dx}\right) \\ $$$$\mathrm{g}'\left(\mathrm{y}\right)\:=\:\mathrm{2xy}\:−\mathrm{2yx}\:=\:\mathrm{0}\:\Rightarrow\mathrm{g}\left(\mathrm{y}\right)\:=\:\mathrm{k} \\ $$$$\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)\:=\:\int\:\left(\mathrm{y}^{\mathrm{2}} −\mathrm{e}^{\mathrm{2x}} \right)\:\mathrm{dx}\:+\:\mathrm{k} \\ $$$$\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)\:=\:\mathrm{xy}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} +\:\mathrm{k}\: \\ $$$$\mathrm{solution}\:\mathrm{is}\:\mathrm{xy}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} +\mathrm{k}\:=\:\mathrm{C} \\ $$$$\mathrm{or}\:\mathrm{xy}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} \:=\:\mathrm{C}_{\mathrm{1}} \\ $$

Commented by bemath last updated on 10/Jun/20

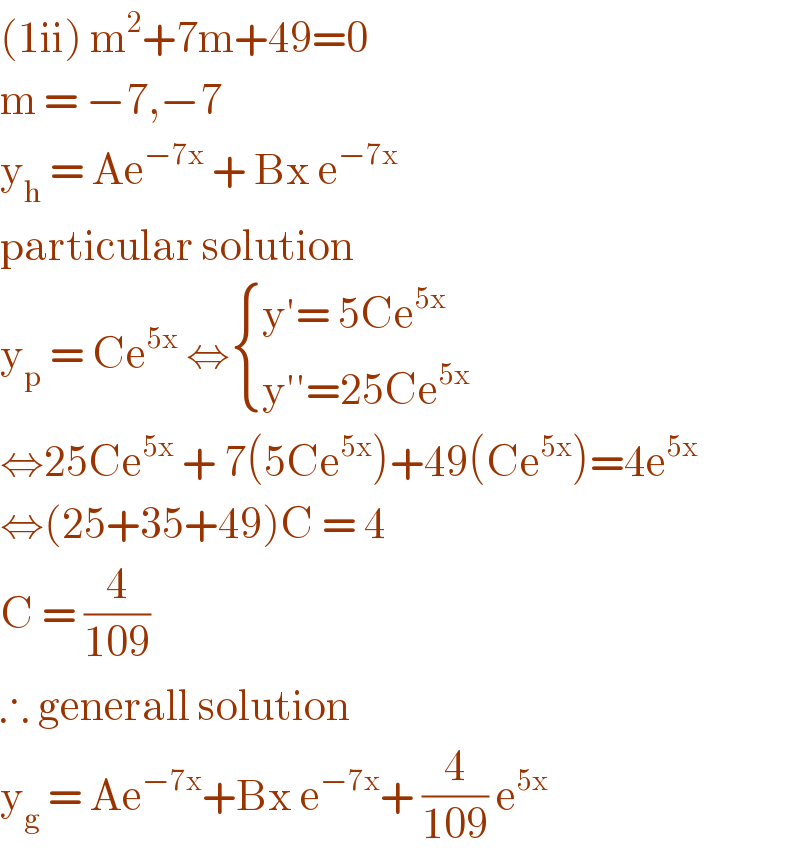
(1ii) m^2 +7m+49=0 m = −7,−7 y_h = Ae^(−7x) + Bx e^(−7x) particular solution y_p = Ce^(5x) ⇔ { ((y′= 5Ce^(5x) )),((y′′=25Ce^(5x) )) :} ⇔25Ce^(5x) + 7(5Ce^(5x) )+49(Ce^(5x) )=4e^(5x) ⇔(25+35+49)C = 4 C = (4/(109)) ∴ generall solution y_g = Ae^(−7x) +Bx e^(−7x) + (4/(109)) e^(5x)

$$\left(\mathrm{1ii}\right)\:\mathrm{m}^{\mathrm{2}} +\mathrm{7m}+\mathrm{49}=\mathrm{0} \\ $$$$\mathrm{m}\:=\:−\mathrm{7},−\mathrm{7} \\ $$$$\mathrm{y}_{\mathrm{h}} \:=\:\mathrm{Ae}^{−\mathrm{7x}} \:+\:\mathrm{Bx}\:\mathrm{e}^{−\mathrm{7x}} \\ $$$$\mathrm{particular}\:\mathrm{solution} \\ $$$$\mathrm{y}_{\mathrm{p}} \:=\:\mathrm{Ce}^{\mathrm{5x}} \:\Leftrightarrow\begin{cases}{\mathrm{y}'=\:\mathrm{5Ce}^{\mathrm{5x}} }\\{\mathrm{y}''=\mathrm{25Ce}^{\mathrm{5x}} }\end{cases} \\ $$$$\Leftrightarrow\mathrm{25Ce}^{\mathrm{5x}} \:+\:\mathrm{7}\left(\mathrm{5Ce}^{\mathrm{5x}} \right)+\mathrm{49}\left(\mathrm{Ce}^{\mathrm{5x}} \right)=\mathrm{4e}^{\mathrm{5x}} \\ $$$$\Leftrightarrow\left(\mathrm{25}+\mathrm{35}+\mathrm{49}\right)\mathrm{C}\:=\:\mathrm{4} \\ $$$$\mathrm{C}\:=\:\frac{\mathrm{4}}{\mathrm{109}} \\ $$$$\therefore\:\mathrm{generall}\:\mathrm{solution} \\ $$$$\mathrm{y}_{\mathrm{g}} \:=\:\mathrm{Ae}^{−\mathrm{7x}} +\mathrm{Bx}\:\mathrm{e}^{−\mathrm{7x}} +\:\frac{\mathrm{4}}{\mathrm{109}}\:\mathrm{e}^{\mathrm{5x}} \: \\ $$

Commented by me2love2math last updated on 10/Jun/20

Thanks all. well appreciated....remain 5

$${Thanks}\:{all}.\:{well}\:{appreciated}....{remain}\:\mathrm{5} \\ $$

Answered by john santu last updated on 10/Jun/20

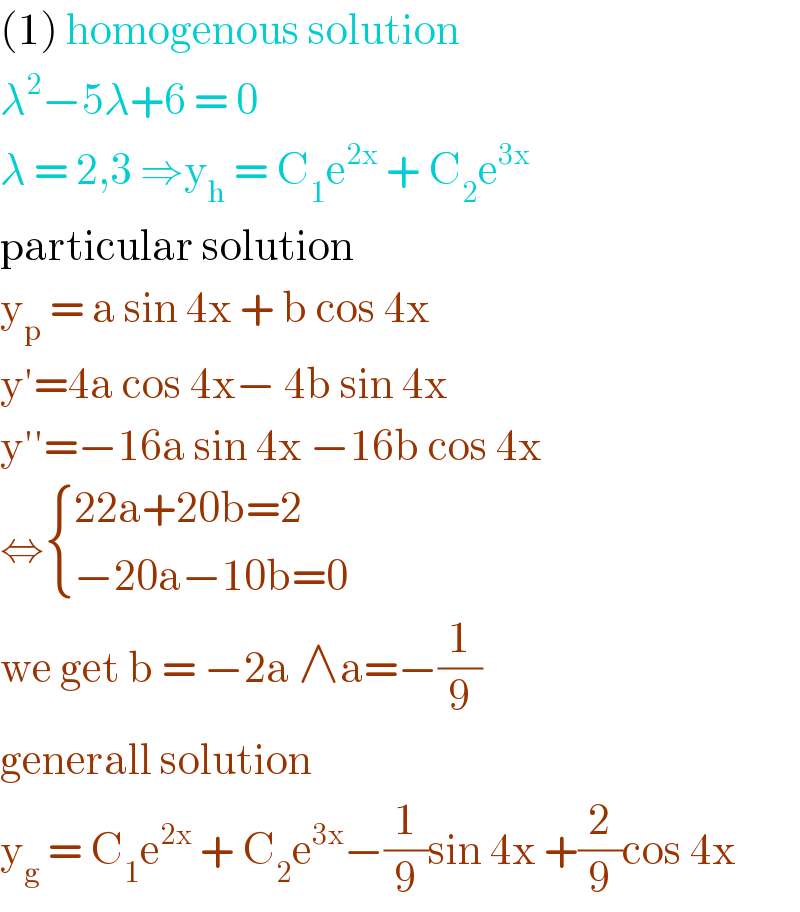
(1) homogenous solution λ^2 −5λ+6 = 0 λ = 2,3 ⇒y_h = C_1 e^(2x) + C_2 e^(3x) particular solution y_p = a sin 4x + b cos 4x y′=4a cos 4x− 4b sin 4x y′′=−16a sin 4x −16b cos 4x ⇔ { ((22a+20b=2)),((−20a−10b=0)) :} we get b = −2a ∧a=−(1/9) generall solution y_g = C_1 e^(2x) + C_2 e^(3x) −(1/9)sin 4x +(2/9)cos 4x

$$\left(\mathrm{1}\right)\:\mathrm{homogenous}\:\mathrm{solution} \\ $$$$\lambda^{\mathrm{2}} −\mathrm{5}\lambda+\mathrm{6}\:=\:\mathrm{0} \\ $$$$\lambda\:=\:\mathrm{2},\mathrm{3}\:\Rightarrow\mathrm{y}_{\mathrm{h}} \:=\:\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\mathrm{2x}} \:+\:\mathrm{C}_{\mathrm{2}} \mathrm{e}^{\mathrm{3x}} \\ $$$$\mathrm{particular}\:\mathrm{solution} \\ $$$$\mathrm{y}_{\mathrm{p}} \:=\:\mathrm{a}\:\mathrm{sin}\:\mathrm{4x}\:+\:\mathrm{b}\:\mathrm{cos}\:\mathrm{4x} \\ $$$$\mathrm{y}'=\mathrm{4a}\:\mathrm{cos}\:\mathrm{4x}−\:\mathrm{4b}\:\mathrm{sin}\:\mathrm{4x} \\ $$$$\mathrm{y}''=−\mathrm{16a}\:\mathrm{sin}\:\mathrm{4x}\:−\mathrm{16b}\:\mathrm{cos}\:\mathrm{4x} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{22a}+\mathrm{20b}=\mathrm{2}}\\{−\mathrm{20a}−\mathrm{10b}=\mathrm{0}}\end{cases} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{b}\:=\:−\mathrm{2a}\:\wedge\mathrm{a}=−\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\mathrm{generall}\:\mathrm{solution} \\ $$$$\mathrm{y}_{\mathrm{g}} \:=\:\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\mathrm{2x}} \:+\:\mathrm{C}_{\mathrm{2}} \mathrm{e}^{\mathrm{3x}} −\frac{\mathrm{1}}{\mathrm{9}}\mathrm{sin}\:\mathrm{4x}\:+\frac{\mathrm{2}}{\mathrm{9}}\mathrm{cos}\:\mathrm{4x}\: \\ $$

Answered by smridha last updated on 10/Jun/20

(6)s^2 x(s)−sx(0)−x^′ (0)−4x(s)=((2s)/(s^2 +4)) x(s)[s^2 −4]−3s−4=((2s)/(s^2 +4)) x(s)=((2s)/((s^2 −4)(s^2 +4))) +(4/(s^2 −2^2 ))+((3s)/(s^2 −2^2 )) x(s)=(s/4)[(1/((s^2 −2^2 )))−(1/((s^2 +2^2 )))]+2[(2/(s^2 −2^2 ))] +3[(s/(s^2 −2^2 ))] now take L^(−1) both sides we get x(t)=(1/4)cosh(2t)−(1/4)cos2t+2sinh(2t) 3cosh(2t) so the solution: x(t)=((13)/4)cosh(2t)−(1/4)cos(2t)+2sinh(2t)

$$\left(\mathrm{6}\right)\boldsymbol{{s}}^{\mathrm{2}} \boldsymbol{{x}}\left(\boldsymbol{{s}}\right)−\boldsymbol{{sx}}\left(\mathrm{0}\right)−\boldsymbol{{x}}^{'} \left(\mathrm{0}\right)−\mathrm{4}\boldsymbol{{x}}\left(\boldsymbol{{s}}\right)=\frac{\mathrm{2}\boldsymbol{{s}}}{\boldsymbol{{s}}^{\mathrm{2}} +\mathrm{4}} \\ $$$$\:\:\:\boldsymbol{{x}}\left(\boldsymbol{{s}}\right)\left[\boldsymbol{{s}}^{\mathrm{2}} −\mathrm{4}\right]−\mathrm{3}\boldsymbol{{s}}−\mathrm{4}=\frac{\mathrm{2}\boldsymbol{{s}}}{\boldsymbol{{s}}^{\mathrm{2}} +\mathrm{4}} \\ $$$$\boldsymbol{{x}}\left(\boldsymbol{{s}}\right)=\frac{\mathrm{2}\boldsymbol{{s}}}{\left(\boldsymbol{{s}}^{\mathrm{2}} −\mathrm{4}\right)\left(\boldsymbol{{s}}^{\mathrm{2}} +\mathrm{4}\right)}\:+\frac{\mathrm{4}}{\boldsymbol{{s}}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{3}{s}}{{s}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} } \\ $$$$\boldsymbol{{x}}\left(\boldsymbol{{s}}\right)=\frac{{s}}{\mathrm{4}}\left[\frac{\mathrm{1}}{\left(\boldsymbol{{s}}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} \right)}−\frac{\mathrm{1}}{\left(\boldsymbol{{s}}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \right)}\right]+\mathrm{2}\left[\frac{\mathrm{2}}{{s}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{3}\left[\frac{{s}}{{s}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }\right] \\ $$$${now}\:{take}\:\boldsymbol{{L}}^{−\mathrm{1}} \:{both}\:{sides}\:{we}\:{get} \\ $$$${x}\left(\boldsymbol{{t}}\right)=\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{{cosh}}\left(\mathrm{2}\boldsymbol{{t}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{t}}+\mathrm{2}\boldsymbol{{sinh}}\left(\mathrm{2}\boldsymbol{{t}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}\boldsymbol{{cosh}}\left(\mathrm{2}\boldsymbol{{t}}\right) \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{the}}\:\boldsymbol{{solution}}: \\ $$$${x}\left(\boldsymbol{{t}}\right)=\frac{\mathrm{13}}{\mathrm{4}}\boldsymbol{{cosh}}\left(\mathrm{2}\boldsymbol{{t}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{{cos}}\left(\mathrm{2}\boldsymbol{{t}}\right)+\mathrm{2}\boldsymbol{{sinh}}\left(\mathrm{2}\boldsymbol{{t}}\right) \\ $$

Commented by smridha last updated on 10/Jun/20

or ans should be like that x(t)=((13)/8)[e^(2t) +e^(−2t) ]+[e^(2t) −e^(−2t) ]−(1/4)cos(2t) =((21)/8)e^(2t) +(5/8)e^(−2t) −(1/4)cos(2t)

$$\boldsymbol{{or}}\:\boldsymbol{{ans}}\:\boldsymbol{{should}}\:\boldsymbol{{be}}\:\boldsymbol{{like}}\:\boldsymbol{{that}} \\ $$$$\boldsymbol{{x}}\left(\boldsymbol{{t}}\right)=\frac{\mathrm{13}}{\mathrm{8}}\left[\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{t}}} +\boldsymbol{{e}}^{−\mathrm{2}\boldsymbol{{t}}} \right]+\left[\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{t}}} −\boldsymbol{{e}}^{−\mathrm{2}\boldsymbol{{t}}} \right]−\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{{cos}}\left(\mathrm{2}\boldsymbol{{t}}\right) \\ $$$$=\frac{\mathrm{21}}{\mathrm{8}}\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{t}}} +\frac{\mathrm{5}}{\mathrm{8}}\boldsymbol{{e}}^{−\mathrm{2}\boldsymbol{{t}}} −\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{{cos}}\left(\mathrm{2}\boldsymbol{{t}}\right) \\ $$

Answered by mathmax by abdo last updated on 10/Jun/20

y^(′′) −5y^′ +6 =2sin(4x) (he)→y^(′′) −5y^′ +6 =0→r^2 −5r +6 =0 Δ =25−24 =1 ⇒r_1 =((5+1)/2) =3 and r_2 =((5−1)/2) =2 ⇒y_h =αe^(3x) +βe^(2x) =α u_1 +β u_2 W(u_1 ,u_2 ) = determinant (((u_1 u_2 )),((u_1 ^′ u_2 ^′ )))= determinant (((e^(3x) e^(2x) )),((3e^(3x) 2e^(2x) )))=−e^(5x) W_1 = determinant (((0 e^(2x) )),((2sin(4x) 2e^(2x) )))=−2e^(2x) sin(4x) W_2 = determinant (((e^(3x) 0)),((3e^(3x) 2sin(4x))))=2e^(3x) sin(4x) v_1 =∫ (w_1 /w)dx =∫ ((−2e^(2x) sin(4x))/(−e^(5x) )) =2∫ e^(−3x) sin(4x)dx =2Im( ∫ e^(−3x+4ix) dx) we have ∫ e^((−3+4i)x) dx =(1/(−3+4i)) e^((−3+4i)x) =−(1/(3−4i))e^(−3x) (cos(4x)+isin(4x)) =−((3+4i)/(25))e^(−3x) (cos(4x)+isin(4x)) =−(1/(25))e^(−3x) (3cos(4x)+3isin(4x)+4icos(4x)−4sin(4x)) ⇒ v_1 =−(2/(25))e^(−3x) (3sin(4x)+4cos(4x)) v_2 =∫ (w_2 /w)dx =∫ ((2e^(3x) sin(4x))/(−e^(5x) ))dx =−2 ∫ e^(−2x) sin(4x)dx =−2 Im( ∫ e^((−2+4i)x) dx) and ∫ e^((−2+4i)x) dx=(1/(−2+4i)) e^((−2+4i)x) =−(1/(2−4i))e^(−2x) (cos(4x)+isin(4x)) =−((2+4i)/(20)) e^(−2x) {cos(4x)+isin(4x)} =−(e^(−2x) /(20)){ 2cos(4x)+2isin(4x)+4icos(4x)−4sin(4x)} ⇒ v_2 =(e^(−2x) /(10))( 2sin(4x)+4cos(4x)} =(e^(−2x) /5)(sin(4x)+2cos(4x)) so y_p =u_1 v_(1 ) +u_2 v_2 =−(2/(25)){3sin(4x)+4cos(4x)} +(1/5)(sin(4x)+2cos(4x)) =(−(6/(25)) +(1/5))sin(4x) +(−(8/(25)) +(2/5))cos(4x) =−(1/(25))sin(4x) +(2/(25)) cos(4x) the general solution is y =y_h +y_p

$$\mathrm{y}^{''} \:−\mathrm{5y}^{'} \:+\mathrm{6}\:=\mathrm{2sin}\left(\mathrm{4x}\right) \\ $$$$\left(\mathrm{he}\right)\rightarrow\mathrm{y}^{''} −\mathrm{5y}^{'} \:+\mathrm{6}\:=\mathrm{0}\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{5r}\:+\mathrm{6}\:=\mathrm{0} \\ $$$$\Delta\:=\mathrm{25}−\mathrm{24}\:=\mathrm{1}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\frac{\mathrm{5}+\mathrm{1}}{\mathrm{2}}\:=\mathrm{3}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\frac{\mathrm{5}−\mathrm{1}}{\mathrm{2}}\:=\mathrm{2}\:\Rightarrow\mathrm{y}_{\mathrm{h}} =\alpha\mathrm{e}^{\mathrm{3x}} \:+\beta\mathrm{e}^{\mathrm{2x}} \\ $$$$=\alpha\:\mathrm{u}_{\mathrm{1}} \:+\beta\:\mathrm{u}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} \:,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{u}_{\mathrm{1}} \:\:\:\:\:\:\:\:\:\:\mathrm{u}_{\mathrm{2}} }\\{\mathrm{u}_{\mathrm{1}} ^{'} \:\:\:\:\:\:\:\:\:\:\mathrm{u}_{\mathrm{2}} ^{'} }\end{vmatrix}=\begin{vmatrix}{\mathrm{e}^{\mathrm{3x}} \:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{2x}} }\\{\mathrm{3e}^{\mathrm{3x}} \:\:\:\:\:\:\:\mathrm{2e}^{\mathrm{2x}} \:}\end{vmatrix}=−\mathrm{e}^{\mathrm{5x}} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{2x}} }\\{\mathrm{2sin}\left(\mathrm{4x}\right)\:\:\:\:\:\:\:\:\:\:\:\mathrm{2e}^{\mathrm{2x}} }\end{vmatrix}=−\mathrm{2e}^{\mathrm{2x}} \:\mathrm{sin}\left(\mathrm{4x}\right) \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{3x}} \:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{3e}^{\mathrm{3x}} \:\:\:\:\:\:\mathrm{2sin}\left(\mathrm{4x}\right)}\end{vmatrix}=\mathrm{2e}^{\mathrm{3x}} \:\mathrm{sin}\left(\mathrm{4x}\right) \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\:\:\frac{−\mathrm{2e}^{\mathrm{2x}} \:\mathrm{sin}\left(\mathrm{4x}\right)}{−\mathrm{e}^{\mathrm{5x}} }\:=\mathrm{2}\int\:\mathrm{e}^{−\mathrm{3x}} \:\mathrm{sin}\left(\mathrm{4x}\right)\mathrm{dx} \\ $$$$=\mathrm{2Im}\left(\:\int\:\mathrm{e}^{−\mathrm{3x}+\mathrm{4ix}} \mathrm{dx}\right)\:\mathrm{we}\:\mathrm{have}\:\int\:\mathrm{e}^{\left(−\mathrm{3}+\mathrm{4i}\right)\mathrm{x}} \:\mathrm{dx}\:=\frac{\mathrm{1}}{−\mathrm{3}+\mathrm{4i}}\:\mathrm{e}^{\left(−\mathrm{3}+\mathrm{4i}\right)\mathrm{x}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}−\mathrm{4i}}\mathrm{e}^{−\mathrm{3x}} \left(\mathrm{cos}\left(\mathrm{4x}\right)+\mathrm{isin}\left(\mathrm{4x}\right)\right)\:=−\frac{\mathrm{3}+\mathrm{4i}}{\mathrm{25}}\mathrm{e}^{−\mathrm{3x}} \left(\mathrm{cos}\left(\mathrm{4x}\right)+\mathrm{isin}\left(\mathrm{4x}\right)\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{25}}\mathrm{e}^{−\mathrm{3x}} \left(\mathrm{3cos}\left(\mathrm{4x}\right)+\mathrm{3isin}\left(\mathrm{4x}\right)+\mathrm{4icos}\left(\mathrm{4x}\right)−\mathrm{4sin}\left(\mathrm{4x}\right)\right)\:\Rightarrow \\ $$$$\mathrm{v}_{\mathrm{1}} =−\frac{\mathrm{2}}{\mathrm{25}}\mathrm{e}^{−\mathrm{3x}} \left(\mathrm{3sin}\left(\mathrm{4x}\right)+\mathrm{4cos}\left(\mathrm{4x}\right)\right) \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\:\frac{\mathrm{2e}^{\mathrm{3x}} \:\mathrm{sin}\left(\mathrm{4x}\right)}{−\mathrm{e}^{\mathrm{5x}} }\mathrm{dx}\:=−\mathrm{2}\:\int\:\:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{sin}\left(\mathrm{4x}\right)\mathrm{dx} \\ $$$$=−\mathrm{2}\:\mathrm{Im}\left(\:\int\:\mathrm{e}^{\left(−\mathrm{2}+\mathrm{4i}\right)\mathrm{x}} \mathrm{dx}\right)\:\mathrm{and}\:\int\:\mathrm{e}^{\left(−\mathrm{2}+\mathrm{4i}\right)\mathrm{x}} \mathrm{dx}=\frac{\mathrm{1}}{−\mathrm{2}+\mathrm{4i}}\:\mathrm{e}^{\left(−\mathrm{2}+\mathrm{4i}\right)\mathrm{x}} \: \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}−\mathrm{4i}}\mathrm{e}^{−\mathrm{2x}} \left(\mathrm{cos}\left(\mathrm{4x}\right)+\mathrm{isin}\left(\mathrm{4x}\right)\right)\:=−\frac{\mathrm{2}+\mathrm{4i}}{\mathrm{20}}\:\mathrm{e}^{−\mathrm{2x}} \:\left\{\mathrm{cos}\left(\mathrm{4x}\right)+\mathrm{isin}\left(\mathrm{4x}\right)\right\} \\ $$$$=−\frac{\mathrm{e}^{−\mathrm{2x}} }{\mathrm{20}}\left\{\:\mathrm{2cos}\left(\mathrm{4x}\right)+\mathrm{2isin}\left(\mathrm{4x}\right)+\mathrm{4icos}\left(\mathrm{4x}\right)−\mathrm{4sin}\left(\mathrm{4x}\right)\right\}\:\Rightarrow \\ $$$$\mathrm{v}_{\mathrm{2}} =\frac{\mathrm{e}^{−\mathrm{2x}} }{\mathrm{10}}\left(\:\mathrm{2sin}\left(\mathrm{4x}\right)+\mathrm{4cos}\left(\mathrm{4x}\right)\right\}\:=\frac{\mathrm{e}^{−\mathrm{2x}} }{\mathrm{5}}\left(\mathrm{sin}\left(\mathrm{4x}\right)+\mathrm{2cos}\left(\mathrm{4x}\right)\right)\:\mathrm{so}\: \\ $$$$\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}\:} +\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} =−\frac{\mathrm{2}}{\mathrm{25}}\left\{\mathrm{3sin}\left(\mathrm{4x}\right)+\mathrm{4cos}\left(\mathrm{4x}\right)\right\}\:+\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{sin}\left(\mathrm{4x}\right)+\mathrm{2cos}\left(\mathrm{4x}\right)\right) \\ $$$$=\left(−\frac{\mathrm{6}}{\mathrm{25}}\:+\frac{\mathrm{1}}{\mathrm{5}}\right)\mathrm{sin}\left(\mathrm{4x}\right)\:+\left(−\frac{\mathrm{8}}{\mathrm{25}}\:+\frac{\mathrm{2}}{\mathrm{5}}\right)\mathrm{cos}\left(\mathrm{4x}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{25}}\mathrm{sin}\left(\mathrm{4x}\right)\:+\frac{\mathrm{2}}{\mathrm{25}}\:\mathrm{cos}\left(\mathrm{4x}\right)\:\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$$$ \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 10/Jun/20

4) let solve by laplace transform y^(′′) +3y^′ +2y =sin(2x) ⇒L(y^(′′) )+3L(y^′ )+2L(y) =L(sin(2x)) ⇒ x^2 L(y)−xy(0)−y^′ (o) +3(xL(y)−y(0))+2L(y) =L(sin(2x)) ⇒ (x^2 +3x+2)L(y) −(x+3)y(o)−y^′ (0) =L(sin(2x)) L(sin(2x) =∫_0 ^∞ sin(2t)e^(−xt) dt =Im(∫_0 ^∞ e^(2it−xt) dt) ∫_0 ^∞ e^((−x+2i)t) dt =[(1/(−x+2i)) e^((−x+2i)t) ]_(t=0) ^∞ =((−1)/(−x+2i)) =(1/(x−2i)) =((x+2i)/(x^2 +4)) ⇒ L(sin(2x))=(2/(x^2 +4)) (e)⇒(x^2 +3x+2)L(y) =y(o)(x+3)+y^′ (0)+(2/(x^2 +4)) ⇒ L(y) =((x+3)/(x^2 +3x+2))y(0) +((y^′ (0))/(x^2 +3x+2)) +(2/((x^2 +3x+2)(x^2 +4))) ⇒ y(x) =y(0)L^(−1) (((x+3)/(x^2 +3x+2)))+y^′ (0)L^(−1) ((1/(x^2 +3x+2)))+2L^(−1) ((1/((x^2 +3x+2)(x^2 +4)))) f(x) =((x+3)/(x^2 +3x+2))=((x+3)/((x+1)(x+2))) =(x+3)((1/(x+1))−(1/(x+2))) =((x+3)/(x+1))−((x+3)/(x+2)) =1+(2/(x+1))−(1+(1/(x+2))) =(2/(x+1))−(1/(x+2)) ⇒ L^(−1) (f) =2e^(−x) −e^(−2x) g(x) =(1/(x^2 +3x+2)) =(1/(x+1))−(1/(x+2)) ⇒L^(−1) (g) =e^(−x) −e^(−2x) h(x) =(1/((x^2 +3x+2)(x^2 +4))) =(1/((x+1)(x+2)(x−2i)(x+2i))) =(a/(x+1)) +(b/(x+2)) +(c/(x−2i)) +(d/(x+2i)) a =(1/((−1−2i)(−1+2i))) =(1/((1+2i)(1−2i))) =(1/5) b =((−1)/((−2−2i)(−2+2i))) =(1/((2+2i)(2−2i))) =(1/(4×2))=(1/8) c =(1/((2i+1)(2i+2)4i)) =(1/(4i(−4+4i+2i+2))) =(1/(4i(−2+6i))) =(1/(−8i−24)) =((−1)/(8i+24)) d =(1/((−2i+1)(−2i+2)(−4i))) =.... L^(−1) (h) =a e^(−x) +b^(−2x) +c e^(2ix) +d e^(−2ix) →at form a e^(−x) +be^(−2x) +αcos(2x) +βsin(2x) so the general solution is y(x) =ae^(−x) +b e^(−2x) +αcos(2x) +βsin(2x)

$$\left.\mathrm{4}\right)\:\mathrm{let}\:\mathrm{solve}\:\mathrm{by}\:\mathrm{laplace}\:\mathrm{transform} \\ $$$$\mathrm{y}^{''} \:+\mathrm{3y}^{'} \:+\mathrm{2y}\:=\mathrm{sin}\left(\mathrm{2x}\right)\:\Rightarrow\mathrm{L}\left(\mathrm{y}^{''} \right)+\mathrm{3L}\left(\mathrm{y}^{'} \right)+\mathrm{2L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{sin}\left(\mathrm{2x}\right)\right)\:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{2}} \:\mathrm{L}\left(\mathrm{y}\right)−\mathrm{xy}\left(\mathrm{0}\right)−\mathrm{y}^{'} \left(\mathrm{o}\right)\:+\mathrm{3}\left(\mathrm{xL}\left(\mathrm{y}\right)−\mathrm{y}\left(\mathrm{0}\right)\right)+\mathrm{2L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{sin}\left(\mathrm{2x}\right)\right)\:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{2}\right)\mathrm{L}\left(\mathrm{y}\right)\:−\left(\mathrm{x}+\mathrm{3}\right)\mathrm{y}\left(\mathrm{o}\right)−\mathrm{y}^{'} \left(\mathrm{0}\right)\:=\mathrm{L}\left(\mathrm{sin}\left(\mathrm{2x}\right)\right) \\ $$$$\mathrm{L}\left(\mathrm{sin}\left(\mathrm{2x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{sin}\left(\mathrm{2t}\right)\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt}\:=\mathrm{Im}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\mathrm{2it}−\mathrm{xt}} \:\mathrm{dt}\right)\right. \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{2i}\right)\mathrm{t}} \:\mathrm{dt}\:=\left[\frac{\mathrm{1}}{−\mathrm{x}+\mathrm{2i}}\:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{2i}\right)\mathrm{t}} \right]_{\mathrm{t}=\mathrm{0}} ^{\infty} \:=\frac{−\mathrm{1}}{−\mathrm{x}+\mathrm{2i}}\:=\frac{\mathrm{1}}{\mathrm{x}−\mathrm{2i}}\:=\frac{\mathrm{x}+\mathrm{2i}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}}\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{sin}\left(\mathrm{2x}\right)\right)=\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}} \\ $$$$\left(\mathrm{e}\right)\Rightarrow\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}+\mathrm{2}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{y}\left(\mathrm{o}\right)\left(\mathrm{x}+\mathrm{3}\right)+\mathrm{y}^{'} \left(\mathrm{0}\right)+\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}}\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{y}\right)\:=\frac{\mathrm{x}+\mathrm{3}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}+\mathrm{2}}\mathrm{y}\left(\mathrm{0}\right)\:+\frac{\mathrm{y}^{'} \left(\mathrm{0}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}+\mathrm{2}}\:+\frac{\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}+\mathrm{2}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{y}\left(\mathrm{0}\right)\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{x}+\mathrm{3}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}+\mathrm{2}}\right)+\mathrm{y}^{'} \left(\mathrm{0}\right)\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}+\mathrm{2}}\right)+\mathrm{2L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}+\mathrm{2}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)}\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}+\mathrm{3}}{\mathrm{x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{2}}=\frac{\mathrm{x}+\mathrm{3}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)}\:=\left(\mathrm{x}+\mathrm{3}\right)\left(\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{x}+\mathrm{3}}{\mathrm{x}+\mathrm{1}}−\frac{\mathrm{x}+\mathrm{3}}{\mathrm{x}+\mathrm{2}}\:=\mathrm{1}+\frac{\mathrm{2}}{\mathrm{x}+\mathrm{1}}−\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2}}\right)\:=\frac{\mathrm{2}}{\mathrm{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\mathrm{f}\right)\:=\mathrm{2e}^{−\mathrm{x}} −\mathrm{e}^{−\mathrm{2x}} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2}}\:\Rightarrow\mathrm{L}^{−\mathrm{1}} \left(\mathrm{g}\right)\:=\mathrm{e}^{−\mathrm{x}} −\mathrm{e}^{−\mathrm{2x}} \\ $$$$\mathrm{h}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}+\mathrm{2}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)}\:=\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}−\mathrm{2i}\right)\left(\mathrm{x}+\mathrm{2i}\right)} \\ $$$$=\frac{\mathrm{a}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{b}}{\mathrm{x}+\mathrm{2}}\:+\frac{\mathrm{c}}{\mathrm{x}−\mathrm{2i}}\:+\frac{\mathrm{d}}{\mathrm{x}+\mathrm{2i}} \\ $$$$\mathrm{a}\:=\frac{\mathrm{1}}{\left(−\mathrm{1}−\mathrm{2i}\right)\left(−\mathrm{1}+\mathrm{2i}\right)}\:=\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{2i}\right)\left(\mathrm{1}−\mathrm{2i}\right)}\:=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\mathrm{b}\:=\frac{−\mathrm{1}}{\left(−\mathrm{2}−\mathrm{2i}\right)\left(−\mathrm{2}+\mathrm{2i}\right)}\:=\frac{\mathrm{1}}{\left(\mathrm{2}+\mathrm{2i}\right)\left(\mathrm{2}−\mathrm{2i}\right)}\:=\frac{\mathrm{1}}{\mathrm{4}×\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\mathrm{c}\:=\frac{\mathrm{1}}{\left(\mathrm{2i}+\mathrm{1}\right)\left(\mathrm{2i}+\mathrm{2}\right)\mathrm{4i}}\:=\frac{\mathrm{1}}{\mathrm{4i}\left(−\mathrm{4}+\mathrm{4i}+\mathrm{2i}+\mathrm{2}\right)}\:=\frac{\mathrm{1}}{\mathrm{4i}\left(−\mathrm{2}+\mathrm{6i}\right)}\:=\frac{\mathrm{1}}{−\mathrm{8i}−\mathrm{24}}\:=\frac{−\mathrm{1}}{\mathrm{8i}+\mathrm{24}} \\ $$$$\mathrm{d}\:=\frac{\mathrm{1}}{\left(−\mathrm{2i}+\mathrm{1}\right)\left(−\mathrm{2i}+\mathrm{2}\right)\left(−\mathrm{4i}\right)}\:=.... \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\mathrm{h}\right)\:=\mathrm{a}\:\mathrm{e}^{−\mathrm{x}} \:+\mathrm{b}^{−\mathrm{2x}} \:+\mathrm{c}\:\mathrm{e}^{\mathrm{2ix}} \:+\mathrm{d}\:\mathrm{e}^{−\mathrm{2ix}} \:\rightarrow\mathrm{at}\:\mathrm{form}\:\mathrm{a}\:\mathrm{e}^{−\mathrm{x}} \:\:+\mathrm{be}^{−\mathrm{2x}} \:+\alpha\mathrm{cos}\left(\mathrm{2x}\right) \\ $$$$+\beta\mathrm{sin}\left(\mathrm{2x}\right)\:\:\mathrm{so}\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{ae}^{−\mathrm{x}} \:+\mathrm{b}\:\mathrm{e}^{−\mathrm{2x}} \:+\alpha\mathrm{cos}\left(\mathrm{2x}\right)\:+\beta\mathrm{sin}\left(\mathrm{2x}\right) \\ $$

Answered by mathmax by abdo last updated on 10/Jun/20

{ ((x^′ =x−2y ⇒ ((x^′ ),(y^′ ) )=A ((x),(y) ))),((y^′ =−2x +y)) :} with A = (((1 −2)),((−2 1)) ) let X = ((x),(h) ) e ⇒X^′ =A X ⇒ X (t)=k e^(A(t−t_0 )) let find e^(tA) p_c (A) =det(A−xI) = determinant (((1−x −2)),((−2 1−x)))=(1−x)^2 −4 =(1−x−2)(1−x+2) =(−x−1)(3−x) =(x+1)(x−3) so the values are λ_1 =−1 and λ_2 =3 x^n =p_c (x)q +u_n x +v_n ⇒(−1)^n =−u_n +v_n and 3^n =3u_n +v_n ⇒ 4u_n =3^n −(−1)^n ⇒ u_n =(((3)^n −(−1)^n )/4) v_n =u_n +(−1)^n =((3^n −(−1)^n )/4) +(−1)^n =((3^n −(−1)^n +4(−1)^n )/4) =((3^n +3(−1)^n )/4) A^n =u_n A +v_n I=((3^n −(−1)^n )/4) (((1 −2)),((−2 1)) ) +((3^n +3(−1)^n )/4) (((1 0)),((0 1)) ) =(1/4) (((3^n −(−1)^n −2(3^n −(−1)^n ))),((−2(3^n −(−1)^n 3^n −(−1)^n )) ) +(1/4) (((3^n +3(−1)^n 0 )),((0 3^n +3(−1)^n )) ) =(1/4) (((2.3^n +2(−1)^n −2.3^n +2(−1)^n )),((−2.3^n +2(−1)^n 2.3^n +2(−1)^n )) ) e^(tA ) =Σ_(n=0) ^∞ (t^n /(n!)) A^n =(1/4)Σ_(n=0) ^∞ (t^n /(n!)) (((2.3^n +2(−1)^n −2.3^n +2(−1)^n )),((−2.3^n +2(−1)^n 2.3^n +2(−1)^n )) ) =(1/2) Σ_(n=0) ^∞ (t^n /(n!)) (((3^n +(−1)^n −3^n +(−1)^n )),((−3^n +(−1)^n 3^n +(−1)^n )) ) =(1/2) ((( Σ_(n=0) ^∞ (((3t)^n )/(n!)) +Σ_(n=0) ^∞ (((−t)^n )/(n!)) −Σ_(n=0) ^∞ (((3t)^n )/(n!))+Σ_(n=0) ^∞ (((−t)^n )/(n!)))),((...... ....)) ) =(1/2) (((e^(3t) +e^(−t) −e^(3t) +e^(−t) )),((−e^(3t) +e^(−t) e^(3t) +e^(−t) )) ) X(t) =k e^(A(t−t_0 ))

$$\begin{cases}{\mathrm{x}^{'} \:=\mathrm{x}−\mathrm{2y}\:\:\Rightarrow\:\:\:\:\:\:\:\:\:\begin{pmatrix}{\mathrm{x}^{'} }\\{\mathrm{y}^{'} }\end{pmatrix}=\mathrm{A}\:\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\end{pmatrix}}\\{\mathrm{y}^{'} =−\mathrm{2x}\:+\mathrm{y}}\end{cases}\:\:\:\mathrm{with}\:\:\mathrm{A}\:=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:−\mathrm{2}}\\{−\mathrm{2}\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$\mathrm{let}\:\mathrm{X}\:=\begin{pmatrix}{\mathrm{x}}\\{\mathrm{h}}\end{pmatrix}\:\:\:\:\mathrm{e}\:\Rightarrow\mathrm{X}^{'} \:=\mathrm{A}\:\mathrm{X}\:\Rightarrow \\ $$$$\mathrm{X}\:\left(\mathrm{t}\right)=\mathrm{k}\:\mathrm{e}^{\mathrm{A}\left(\mathrm{t}−\mathrm{t}_{\mathrm{0}} \right)} \:\mathrm{let}\:\mathrm{find}\:\:\:\mathrm{e}^{\mathrm{tA}} \\ $$$$\mathrm{p}_{\mathrm{c}} \left(\mathrm{A}\right)\:=\mathrm{det}\left(\mathrm{A}−\mathrm{xI}\right)\:=\begin{vmatrix}{\mathrm{1}−\mathrm{x}\:\:\:\:\:\:\:−\mathrm{2}}\\{−\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{1}−\mathrm{x}}\end{vmatrix}=\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} −\mathrm{4}\:=\left(\mathrm{1}−\mathrm{x}−\mathrm{2}\right)\left(\mathrm{1}−\mathrm{x}+\mathrm{2}\right) \\ $$$$=\left(−\mathrm{x}−\mathrm{1}\right)\left(\mathrm{3}−\mathrm{x}\right)\:=\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{3}\right)\:\:\mathrm{so}\:\mathrm{the}\:\mathrm{values}\:\mathrm{are}\:\lambda_{\mathrm{1}} =−\mathrm{1}\:\mathrm{and}\:\lambda_{\mathrm{2}} =\mathrm{3} \\ $$$$\mathrm{x}^{\mathrm{n}} \:=\mathrm{p}_{\mathrm{c}} \left(\mathrm{x}\right)\mathrm{q}\:+\mathrm{u}_{\mathrm{n}} \mathrm{x}\:+\mathrm{v}_{\mathrm{n}} \:\Rightarrow\left(−\mathrm{1}\right)^{\mathrm{n}} \:=−\mathrm{u}_{\mathrm{n}} +\mathrm{v}_{\mathrm{n}} \:\mathrm{and}\:\mathrm{3}^{\mathrm{n}} \:=\mathrm{3u}_{\mathrm{n}} \:+\mathrm{v}_{\mathrm{n}} \:\Rightarrow \\ $$$$\mathrm{4u}_{\mathrm{n}} =\mathrm{3}^{\mathrm{n}} −\left(−\mathrm{1}\right)^{\mathrm{n}} \:\Rightarrow\:\mathrm{u}_{\mathrm{n}} =\frac{\left(\mathrm{3}\right)^{\mathrm{n}} −\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{4}} \\ $$$$\mathrm{v}_{\mathrm{n}} =\mathrm{u}_{\mathrm{n}} \:+\left(−\mathrm{1}\right)^{\mathrm{n}} \:=\frac{\mathrm{3}^{\mathrm{n}} −\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{4}}\:+\left(−\mathrm{1}\right)^{\mathrm{n}} \:=\frac{\mathrm{3}^{\mathrm{n}} −\left(−\mathrm{1}\right)^{\mathrm{n}} \:+\mathrm{4}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{4}}\:=\frac{\mathrm{3}^{\mathrm{n}} \:+\mathrm{3}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{4}} \\ $$$$\mathrm{A}^{\mathrm{n}} \:=\mathrm{u}_{\mathrm{n}} \:\mathrm{A}\:+\mathrm{v}_{\mathrm{n}} \mathrm{I}=\frac{\mathrm{3}^{\mathrm{n}} −\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{4}}\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\:−\mathrm{2}}\\{−\mathrm{2}\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\:\:+\frac{\mathrm{3}^{\mathrm{n}} \:+\mathrm{3}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{4}}\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\begin{pmatrix}{\mathrm{3}^{\mathrm{n}} −\left(−\mathrm{1}\right)^{\mathrm{n}} \:\:\:\:−\mathrm{2}\left(\mathrm{3}^{\mathrm{n}} −\left(−\mathrm{1}\right)^{\mathrm{n}} \right)}\\{−\mathrm{2}\left(\mathrm{3}^{\mathrm{n}} −\left(−\mathrm{1}\right)^{\mathrm{n}} \:\:\:\:\:\:\:\mathrm{3}^{\mathrm{n}} −\left(−\mathrm{1}\right)^{\mathrm{n}} \right.}\end{pmatrix}\:+\frac{\mathrm{1}}{\mathrm{4}}\begin{pmatrix}{\mathrm{3}^{\mathrm{n}} \:+\mathrm{3}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\:\:\:\:\:\:\:\mathrm{0}\:\:\:}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{n}} \:+\mathrm{3}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:}\end{pmatrix} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\begin{pmatrix}{\mathrm{2}.\mathrm{3}^{\mathrm{n}} \:+\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}.\mathrm{3}^{\mathrm{n}} \:+\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{n}} }\\{−\mathrm{2}.\mathrm{3}^{\mathrm{n}} \:+\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}.\mathrm{3}^{\mathrm{n}} \:+\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{n}} }\end{pmatrix} \\ $$$$\mathrm{e}^{\mathrm{tA}\:} \:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{n}} }{\mathrm{n}!}\:\mathrm{A}^{\mathrm{n}} \:\:=\frac{\mathrm{1}}{\mathrm{4}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{n}} }{\mathrm{n}!}\:\begin{pmatrix}{\mathrm{2}.\mathrm{3}^{\mathrm{n}} \:+\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}.\mathrm{3}^{\mathrm{n}} \:+\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{n}} }\\{−\mathrm{2}.\mathrm{3}^{\mathrm{n}} \:+\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\:\:\:\:\:\:\:\:\:\:\mathrm{2}.\mathrm{3}^{\mathrm{n}} \:+\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{n}} }\end{pmatrix} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{n}} }{\mathrm{n}!}\:\begin{pmatrix}{\mathrm{3}^{\mathrm{n}} \:+\left(−\mathrm{1}\right)^{\mathrm{n}} \:\:\:\:\:\:\:\:\:\:\:−\mathrm{3}^{\mathrm{n}} \:+\left(−\mathrm{1}\right)^{\mathrm{n}} }\\{−\mathrm{3}^{\mathrm{n}} \:+\left(−\mathrm{1}\right)^{\mathrm{n}} \:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{n}} \:+\left(−\mathrm{1}\right)^{\mathrm{n}} }\end{pmatrix} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{3t}\right)^{\mathrm{n}} }{\mathrm{n}!}\:+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{t}\right)^{\mathrm{n}} }{\mathrm{n}!}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{3t}\right)^{\mathrm{n}} }{\mathrm{n}!}+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{t}\right)^{\mathrm{n}} }{\mathrm{n}!}}\\{......\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:....}\end{pmatrix} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{\mathrm{e}^{\mathrm{3t}} \:+\mathrm{e}^{−\mathrm{t}} \:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{e}^{\mathrm{3t}} \:+\mathrm{e}^{−\mathrm{t}} \:\:\:\:\:}\\{−\mathrm{e}^{\mathrm{3t}} \:\:+\mathrm{e}^{−\mathrm{t}} \:\:\:\:\:\:\mathrm{e}^{\mathrm{3t}} \:+\mathrm{e}^{−\mathrm{t}} }\end{pmatrix} \\ $$$$\mathrm{X}\left(\mathrm{t}\right)\:=\mathrm{k}\:\mathrm{e}^{\mathrm{A}\left(\mathrm{t}−\mathrm{t}_{\mathrm{0}} \right)} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com